接着上一篇,mindmap更新如下内容。
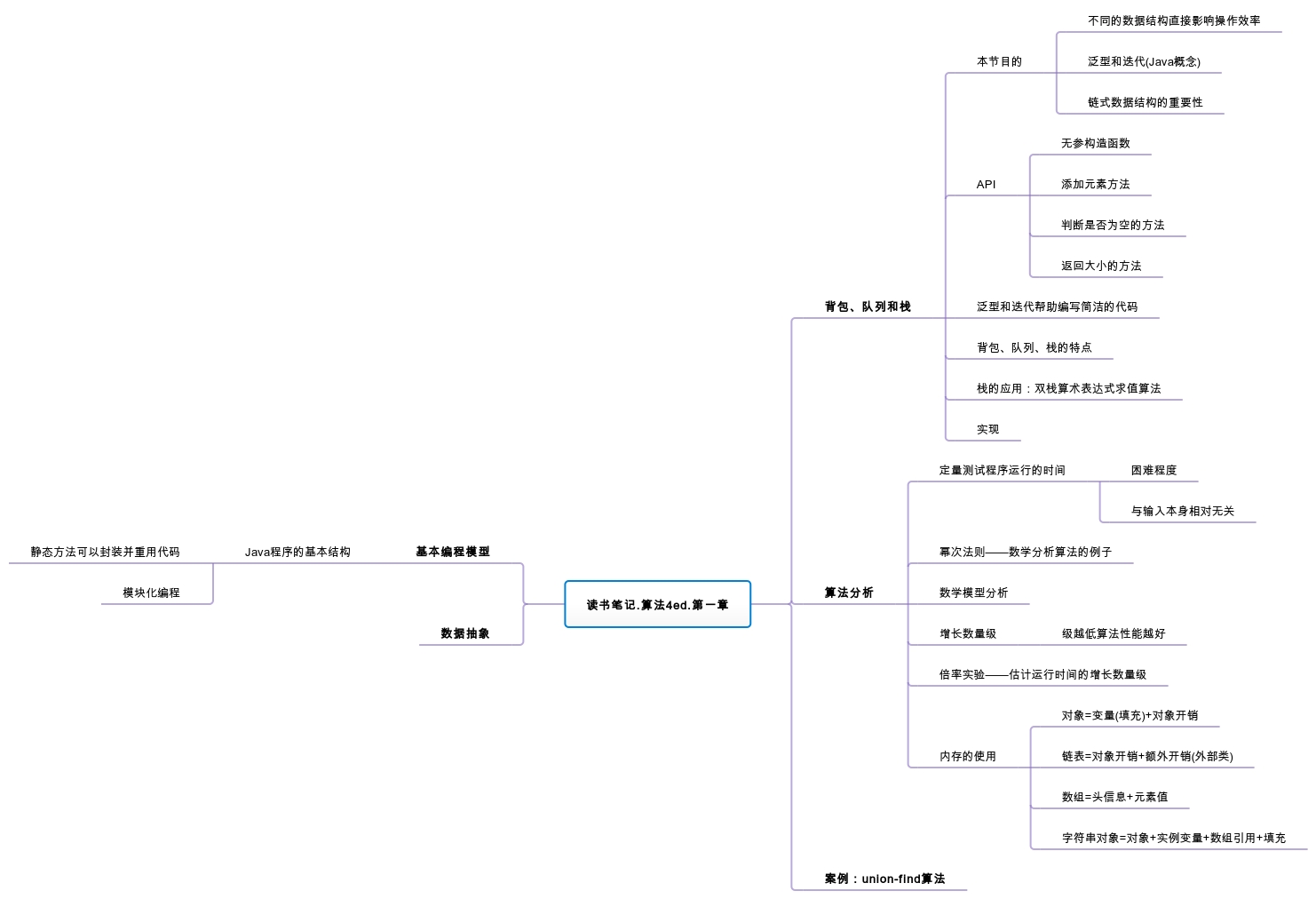
3.背包、队列和栈
这节主要讲述了这三种数据结构(Bag、Queue、Stack)的API、实现以及链表。Queue和Stack还含有删除元素的方法。并引出了泛型,也就是可以用它来存储任何类型的数据。在API中,类class Bag<Item> implements Iterable<Item>的表示就将Item定义为一个类型参数。在创建数据结构时,我们就可以用任何类型代替Item了。有了泛型,我们就只需要一份API来处理所有类型的数据了。这要大大提倡,虽然在一些具体操作上(如删除)API无法表现差异。
这里还提到了Java中的引用类型,即Boolean、Byte、Character、Double、Float、Integer、Long和Short分别对应着boolean、byte、char、double、float、int、long和short(前者为引用数据类型,后者为原始数据类型)。Java对于这两种类型的转换在使用泛型提供了自动装箱/拆箱。接着又写到了迭代(foreach)访问元素,即使用Java语言本身的机制而不依赖数据结构的具体实现。
这三种结构的特点简单描述一下。背包不能删除元素也忽略Add时的顺序。先进先出是队列的特点,而后进先出是栈的特点。书中还介绍了一个应用栈的经典算法——Dijkstra的双栈算术表达式求值算法。他使用了一个操作数栈和一个运算符栈来处理表达式,忽略左括号,在遇到右括号时弹出运算符和所需数量的操作数来进行运算,并将结果压入操作数栈。
用定容栈进行热身,开始实现这三种数据结构。最后得到泛型的可动态调整大小的结构,也介绍了Java的垃圾回收策略,并避免对象游离。当中穿插了怎样用链表作为数据单元。
在这节中的数据结构式整本书的基石,其研究步骤也是全书中研究方法的原型,依次为定义API、开发用例代码、描述一种数据结构并定义类的实例变量、描述算法并实现类的实例方法、分析算法。
4、算法分析
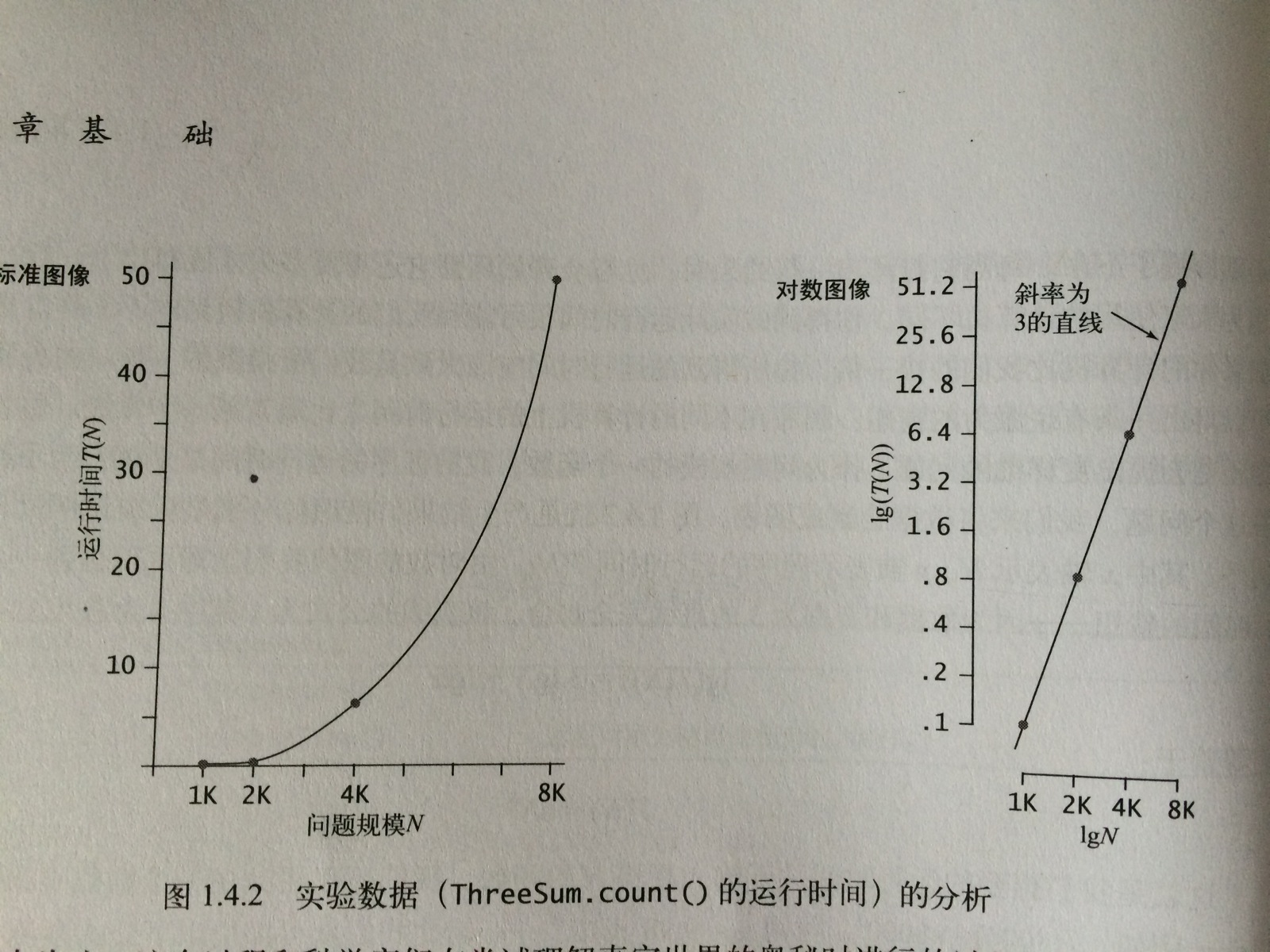
先通过一个记录程序运行实现的计数器的观察,来时间对于分析算法的意义。随后进入了数学时间,书中分别使用了标准比例尺和对数比例尺,在对数比例尺中出现了一条直线,其表达式为lg(T(N)) = 3lgN + lga,多么熟悉的式子,而以前并不知道它的意义是在对数比例下呈现。通过这条直线我们可以预计更大数值的运行实现。对数图像中的直线等价于我们对数据符合公式T(N)=aNb的猜想,这个公式称为幂次法则。许多自然和人工现象都符合这个法则。
这是不是说我们需要一个数学模型来描述算法运行时间呢?当然。度量程序运行时间的就是我们很熟悉的每条语句的耗时和频率,而执行最频繁的指令决定了程序执行的总时间,也就是一小部分指令。那么,我们就化繁为简,只考虑运行时间地增长数量级。忽略了个体机器运算能力的细节使得发表于数十年前的经典算法的性能理论在今天仍然使用。使用成本模型来评估算法的性质,比如访问数组元素的次数。如上就总结出了分析算法的步骤,即确定输入模型(问题规模)、识别内循环、确定成本模型、判断操作的执行频率。
在介绍了增长数量级后,我们把书中的算法分为2类。第一类是解决问题的简单方法,即暴力算法;第二类是降低算法所需时间地增长数量级的改进算法。书中也提醒我们一些需要注意的例外,比如大常数。当然,内存也是应该考虑的元素。最后提醒了一句,在生产代码时不要过于关注程序的性能,首要任务是写出清晰正确的代码。这是不是搬运工的意思?