线性代数有多久神奇?问小学数学去。小学二年级的时候有一类题目让我记忆犹新,说是学校里买了4张桌子和6把椅子一共48块钱,如果买2张桌子和10把椅子一共要52块钱,问桌子多少钱一张,椅子多少钱一把?当时的解法想法讨巧,不知道现在的爸爸妈妈们还记不记得?
小学四年级,学了二元一次方程组,原来这道考试的附加题难道便下降为了普通计算题:
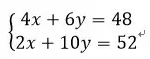
二元一次方程有一些标准的解法,比如代入法、消元法。它使我们可以完全只关心数字而不用再管它们的具体意义。问题的解决有了流程,因为任何一个这样的方程组我们按流程一步步走就可以了,不用再像二年级的时候那样挖空心思去想什么奇巧的方法。没错,这就是数学的意义,通过新的工具和方法,让原来的问题变得更加规范和容易。
二元一次方程的标准解法,让原来问题的难度从5星变成了2星,有没有更容易的方法,难度只有1星?不用到动任何脑子,只要加减乘除,不管是什么方程,一个公式搞定?研究数学的人都是天才,他们还真找到了这样的方法,这就是线性代数。它给我们提供了这样一个公式:
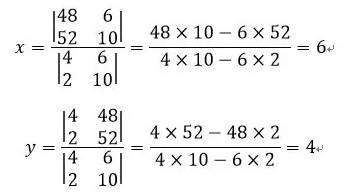
没错,只有加减乘除,不用动一点脑子,计算器按几下就可以得到答案。更加神奇的是,这个公式不只对二元一次方程组有用,对三元一次方程组、四元一次方程组以及随便多少元的一次程组统统有效。觉得公式计算量有点大么?没关系,有计算机啊,计算机最擅长的就是做这种不动脑子死算的事情了。
这种一次方程是我们生活中遇到的最多的,它又称为线性方程。线性代数就从线性方程组发展而来的一整套解题方法,它使我们可以无脑解决任意线性方程组。那么它是怎么做到的呢?这最好从线性代数是怎么来的说起。
对于线性代数的起源我没有作过考证,这不重要,不过要是让我来当这个编剧,剧本应该会是这样的。就像前面的桌子椅子的问题,生活会遇到许许多多类似投入一定数量的各种原料(钱也是原料之一),得到一定数量的各种产品,这些产品又作为原料再生产出下一级的产品的情况。比如我曾经玩过的一个农场的游戏,它的生产链是这样的:
最初级的产品是地里的农作物,它们无需原料,直接生产。如:小麦、玉米、甘蔗。
农作物可以做成动物饲料以生产动物产品。如:2小麦+1玉米=1鸡蛋,1甘蔗+1玉米=1红糖。
还有更高级的产品。如: 2鸡蛋+1红糖=1曲奇。2红糖=1白糖
有人想到可以把这些做成投入产出表:
|
鸡蛋 |
红糖 |
|
|
小麦 |
2 |
0 |
|
玉米 |
1 |
1 |
|
甘蔗 |
0 |
1 |
|
曲奇 |
白糖 |
|
|
鸡蛋 |
2 |
0 |
|
红糖 |
1 |
2 |
再偷懒省去了标题和网络线就写成了被现在称为矩阵的东西:
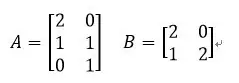
那么自然就会有人想,要生产1个曲奇要多少小麦、玉米和甘蔗,进一步又要问:要生产8个曲奇,10个白糖又要多少小麦、玉米和甘蔗呢?当然你可以把你所需要的曲奇和白糖先转换成鸡蛋和红糖的数量,再把鸡蛋和红糖分别转换成小麦、玉米和甘蔗的数量,最后相加就可以得到你要的结果。但是数学家不会这么想,他们无时无刻不在想有没有捷径可以一步到位。还真被他们发明出来了,那就是矩阵原来可以相乘:
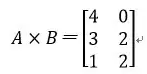
也就是说1个曲奇需要4个小麦、3个玉米和1个甘蔗,1个红糖需要1个玉米和1个甘蔗,如果需要做8个曲奇和10个白糖,就可以这样把两个矩阵相乘:
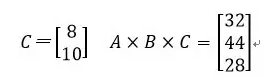
共需要32个小麦44个玉米和28个甘蔗,公式发明出来了,虽然有点长,但好在只需要无脑死算加减乘除就行,有了计算机的帮助更是不在话下。数学家们很得意,他们开创了一个全新的数学领域,这个领域不同于以往的数学,一个公式只能求出一个数字,在线性代数的世界里,等号后面是一个矩阵,也就是许多数字的组合。而且这些公式不管投入和产出的产品种类有多少,永远都是正确的。想像这个农场游戏里可不只有这几样简单的东西,所有的产品加起来有上百种之多,每一种产品又是由几种其它的产品组合生产出来的。这样如果是用原来的方法一级一级的算出来求和,非把人算疯不可。但是用了矩阵乘法,要生产任何东西,不管多少,就是一个连续乘法:X = N x … x D x C x B x A,扔给计算机做,简单优雅轻松愉快!
接下来的问题自然就来了,有了乘法,是不是应该有一个除法呢?或者说有一个倒数,在一个矩阵运算A x B = C里面知道了B和C,马上就知道A是什么。就这就一开始的二元一次方程组:
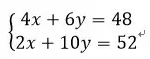
换成矩阵形式就是:

这在初等代数里是很容易实现,因为有除法和倒数。如果我们知道 5×X=10,X就一定是10÷5或者10×0.2,不会错。于是数学家们又开始开动脑筋,要找出线性代数里的除法或者倒数。最后,还真被他们找到了:

把它经过进一步的整理和化简,形成了一开始提到著名的N元一次方程组的万能公式!
人类终于完全征服所有的线性方程组,但线性代数的神奇还不止于此,更宏大的目标还在前方等着我们。
《线性代数》随笔系列首发于微信公众号:龙猫图书馆,这是由猫馆长发起的小资文艺青年聚集之所,欢迎关注。