一、题目:数值的整数次方
题目:实现函数double Power(doublebase, int exponent),求base的exponent次方。不得使用库函数,同时不需要考虑大数问题。
在.NET Framework提供的BCL中,Math类实现了一个Pow方法,例如要求2的三次方,可以通过以下代码实现:
double result = Math.Pow(2, 3);
本题就是要实现一个类似于该Pow方法的功能。
二、解决思路与实现
2.1 不加思索的思路
不需要考虑大数问题,可以在30秒内想到的思路如下:
public double Power(double baseNumber,int exponent) { double result = 1; for (int i = 1; i <= exponent; i++) { result = result * baseNumber; } return result; }
但是,上面的代码没有考虑到输入的指数(exponent)小于1即是零和负数的时候怎么办,它只考虑了指数是正数的情况。
2.2 全面考虑的思路
(1)当指数为负数的时候:可以先对指数求绝对值,然后算出次方的结果之后再取倒数。
(2)当底数(base)是零且指数是负数的时候:通过全局代码或异常告诉调用者参数有误。
(3)0的0次方的时候:由于0的0次方在数学上是没有意义的,因此无论是输出0还是1都是可以接受的。
public static bool isInvalidInput = false; public static double Power(double baseNumber, int exponent) { isInvalidInput = false; // 当底数(base)是零且指数是负数的时候提示参数非法 if (Equals(baseNumber, 0.0) && exponent < 0) { isInvalidInput = true; return 0.0; } uint absExponent = (uint)exponent; if (exponent < 0) { absExponent = (uint)(-1 * exponent); } double result = PowerWithUintExponent(baseNumber, absExponent); // 当指数为负数的时候需算出次方的结果之后再取倒数 if(exponent < 0) { result = 1.0 / result; } return result; } private static double PowerWithUintExponent(double baseNumber, uint exponent) { double result = 1.0; for (int i = 1; i <= exponent; i++) { result = result * baseNumber; } return result; } /// <summary> /// 在判断底数base是不是等于0时,不能直接写base==0, /// 这是因为在计算机内表示小数时(包括float和double型小数)都有误差。 /// </summary> private static bool Equal(double num1, double num2) { if (num1 - num2 > -0.0000001 && num1 - num2 < 0.0000001) { return true; } else { return false; } }
细节:在判断底数baseNumber是不是等于0时,不能直接写baseNumber==0,这是因为在计算机内表示小数时(包括float和double型小数)都有误差。判断两个小数是否相等,只能判断它们之差的绝对值是不是在一个很小的范围内。如果两个数相差很小,就可以认为它们相等。
三、单元测试
3.1 测试用例
// 底数、指数都为正数 [TestMethod] public void PowerTest1() { Assert.AreEqual(PowerHelper.Power(2, 3), 8); } // 底数为负数、指数为正数 [TestMethod] public void PowerTest2() { Assert.AreEqual(PowerHelper.Power(-2, 3), -8); } // 指数为负数 [TestMethod] public void PowerTest3() { Assert.AreEqual(PowerHelper.Power(2, -3), 0.125); } // 指数为0 [TestMethod] public void PowerTest4() { Assert.AreEqual(PowerHelper.Power(2, 0), 1); } // 底数、指数都为0 [TestMethod] public void PowerTest5() { Assert.AreEqual(PowerHelper.Power(0, 0), 1); } // 底数为0、指数为正数 [TestMethod] public void PowerTest6() { Assert.AreEqual(PowerHelper.Power(0, 4), 0); } // 底数为0、指数为负数 [TestMethod] public void PowerTest7() { Assert.AreEqual(PowerHelper.Power(0, -4), 0); Assert.AreEqual(PowerHelper.isInvalidInput, true); }
3.2 测试结果
(1)测试通过结果

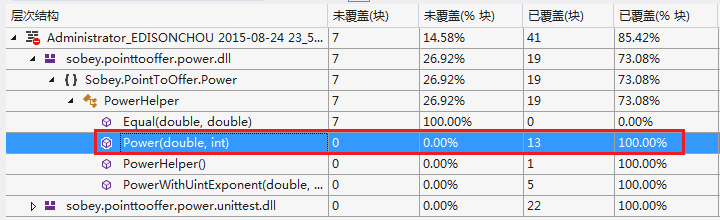
(2)代码覆盖率结果