在上一篇中,我们了解了单链表与双链表,本次将单链表中终端结点的指针端由空指针改为指向头结点,就使整个单链表形成一个环,这种头尾相接的单链表称为单循环链表,简称循环链表(circular linked list)。
一、循环链表基础
1.1 循环链表节点结构

循环链表和单链表的主要差异就在于循环的判断条件上,原来是判断p.next是否为空,现在则是p.next不等于头结点,则循环未结束。
1.2 循环链表的O(1)访问时间
在单链表中,有了头结点,我们可以在O(1)时间访问到第一个节点,但如果要访问最后一个节点却需要O(n)的时间,因为我们需要对整个链表进行一次遍历。在循环链表中,我们可以借助尾节点来实现,即不用头指针,而是用指向终端结点的尾指针来表示循环链表,这时候无论是查找第一个节点还是最后一个节点都很方便,可以控制在O(1)的时间内,如下图所示。

从上图中可以看到,终端结点用尾指针(tail)指示,则查找终端结点是O(1),而开始结点,其实就是tail.Next,其时间复杂也为O(1)。由此也可以联想到,在合并两个循环链表时,只需要修改两个链表的尾指针即可快速地进行合并。
二、循环链表实现
2.1 循环链表节点的定义实现
public class CirNode<T> { public T Item { get; set; } public CirNode<T> Next { get; set; } public CirNode() { } public CirNode(T item) { this.Item = item; } }
这里跟单链表的节点定义实现并无区别。
2.2 循环链表新节点的插入实现
public void Add(T value) { CirNode<T> newNode = new CirNode<T>(value); if (this.tail == null) { // 如果链表当前为空则新元素既是尾头结点也是头结点 this.tail = newNode; this.tail.Next = newNode; this.currentPrev = newNode; } else { // 插入到链表末尾处 newNode.Next = this.tail.Next; this.tail.Next = newNode; // 改变当前节点 if (this.currentPrev == this.tail) { this.currentPrev = newNode; } // 重新指向新的尾节点 this.tail = newNode; } this.count++; }
首先,这里的currentPrev字段是使用了前驱节点来标识当前节点,如要获取当前节点的值可以通过currentPrev.Next.Item来获得。其次,在最后将尾节点指针指向新插入的节点。
2.2 循环链表当前节点的移除实现
public void Remove() { if (this.tail == null) { throw new NullReferenceException("链表中没有任何元素"); } else if (this.count == 1) { // 只有一个元素时将两个指针置为空 this.tail = null; this.currentPrev = null; } else { if (this.currentPrev.Next == this.tail) { this.tail = this.currentPrev; } // 移除当前节点 this.currentPrev.Next = this.currentPrev.Next.Next; } this.count--; }
这里考虑到删除节点时必须寻找其前驱节点会导致链表进行遍历,故使用了当前节点的前驱节点来标识这个当前节点。移除当前节点只需要currentPrev.Next = currentPrev.Next.Next即可。
以下是单循环链表的完整模拟实现代码,需要注意的是该CircularLinkedList主要是为下面的约瑟夫问题而设计,故只实现了一些很简单的功能:

/// <summary> /// 单向循环链表的模拟实现 /// </summary> public class MyCircularLinkedList<T> { private int count; // 字段:记录数据元素个数 private CirNode<T> tail; // 字段:记录尾节点的指针 private CirNode<T> currentPrev; // 字段:使用前驱节点标识当前节点 // 属性:指示链表中元素的个数 public int Count { get { return this.count; } } // 属性:指示当前节点中的元素值 public T CurrentItem { get { return this.currentPrev.Next.Item; } } public MyCircularLinkedList() { this.count = 0; this.tail = null; } public bool IsEmpty() { return this.tail == null; } // Method01:根据索引获取节点 private CirNode<T> GetNodeByIndex(int index) { if (index < 0 || index >= this.count) { throw new ArgumentOutOfRangeException("index", "索引超出范围"); } CirNode<T> tempNode = this.tail.Next; for (int i = 0; i < index; i++) { tempNode = tempNode.Next; } return tempNode; } // Method02:在尾节点后插入新节点 public void Add(T value) { CirNode<T> newNode = new CirNode<T>(value); if (this.tail == null) { // 如果链表当前为空则新元素既是尾头结点也是头结点 this.tail = newNode; this.tail.Next = newNode; this.currentPrev = newNode; } else { // 插入到链表末尾处 newNode.Next = this.tail.Next; this.tail.Next = newNode; // 改变当前节点 if (this.currentPrev == this.tail) { this.currentPrev = newNode; } // 重新指向新的尾节点 this.tail = newNode; } this.count++; } // Method03:移除当前所在节点 public void Remove() { if (this.tail == null) { throw new NullReferenceException("链表中没有任何元素"); } else if (this.count == 1) { // 只有一个元素时将两个指针置为空 this.tail = null; this.currentPrev = null; } else { if (this.currentPrev.Next == this.tail) { // 当删除的是尾指针所指向的节点时 this.tail = this.currentPrev; } // 移除当前节点 this.currentPrev.Next = this.currentPrev.Next.Next; } this.count--; } // Method04:获取所有节点信息 public string GetAllNodes() { if (this.count == 0) { throw new NullReferenceException("链表中没有任何元素"); } else { CirNode<T> tempNode = this.tail.Next; string result = string.Empty; for (int i = 0; i < this.count; i++) { result += tempNode.Item + " "; tempNode = tempNode.Next; } return result; } } }
2.3 单循环链表的简单测试
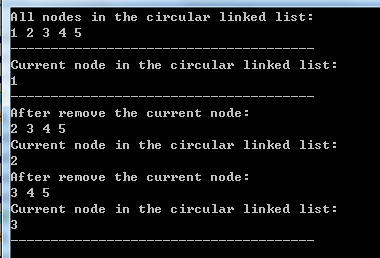
这里的简单测试主要涉及:1.顺序插入5个节点,看节点元素是否正确;2.查看当前节点是否正确;3.移除某个元素,查看当前节点是否正确;测试代码如下所示:
static void MyCircularLinkedListTest() { MyCircularLinkedList<int> linkedList = new MyCircularLinkedList<int>(); // 顺序插入5个节点 linkedList.Add(1); linkedList.Add(2); linkedList.Add(3); linkedList.Add(4); linkedList.Add(5); Console.WriteLine("All nodes in the circular linked list:"); Console.WriteLine(linkedList.GetAllNodes()); Console.WriteLine("--------------------------------------"); // 当前节点:第一个节点 Console.WriteLine("Current node in the circular linked list:"); Console.WriteLine(linkedList.CurrentItem); Console.WriteLine("--------------------------------------"); // 移除当前节点(第一个节点) linkedList.Remove(); Console.WriteLine("After remove the current node:"); Console.WriteLine(linkedList.GetAllNodes()); Console.WriteLine("Current node in the circular linked list:"); Console.WriteLine(linkedList.CurrentItem); // 移除当前节点(第二个节点) linkedList.Remove(); Console.WriteLine("After remove the current node:"); Console.WriteLine(linkedList.GetAllNodes()); Console.WriteLine("Current node in the circular linked list:"); Console.WriteLine(linkedList.CurrentItem); Console.WriteLine("--------------------------------------"); Console.WriteLine(); }
测试结果如下所示:
三、循环链表与约瑟夫问题
3.1 何为约瑟夫问题
据说著名犹太历史学家 Josephus 有过以下的故事:在罗马人占领乔塔帕特后,39 个犹太人与Josephus及他的朋友躲到一个洞中,39个犹太人决定宁愿死也不要被敌人抓到,于是决定了一个自杀方式,41个人排成一个圆圈,由第1个人开始报数,每报数到第3人该人就必须自杀,然后再由下一个重新报数,直到所有人都自杀身亡为止。然而 Josephus 和他的朋友并不想遵从,Josephus 要他的朋友先假装遵从,他将朋友与自己安排在第16个与第31个位置,于是逃过了这场死亡游戏。

以上就是著名的约瑟夫问题:N个人围成一圈,从第一个开始报数,第M个将被杀掉,最后剩下Q个。从围成一圈这里就启发了我们可以使用循环链表来解决该问题。
3.2 使用循环链表解决约瑟夫问题
(1)为CircularLinkedList添加Move()方法实现让当前节点向前移动N步
public void Move(int step = 1) { if (step < 1) { throw new ArgumentOutOfRangeException("step", "移动步数不能小于1"); } for (int i = 1; i < step; i++) { currentPrev = currentPrev.Next; } }
注意到这里循环是从1开始,因为currentPrev是当前节点的前驱节点,而不是真正的当前节点。
(2)在Main()方法中添加测试代码验证是否能够正确让元素出列
static void JosephusTest() { MyCircularLinkedList<int> linkedList = new MyCircularLinkedList<int>(); string result = string.Empty; Console.WriteLine("Step1:请输入人数N"); int n = Convert.ToInt32(Console.ReadLine()); Console.WriteLine("Step2:请输入数字M"); int m = Convert.ToInt32(Console.ReadLine()); Console.WriteLine("Step3:报数游戏开始"); // 添加参与人员元素 for (int i = 1; i <= n; i++) { linkedList.Add(i); } // 打印所有参与人员 Console.Write("所有参与人员:{0}", linkedList.GetAllNodes()); Console.WriteLine(" " + "-------------------------------------"); result = string.Empty; while (linkedList.Count > 1) { // 依次报数:移动 linkedList.Move(m); // 记录出队人员 result += linkedList.CurrentItem + " "; // 移除人员出队 linkedList.Remove(); Console.WriteLine(); Console.Write("剩余报数人员:{0}", linkedList.GetAllNodes()); Console.Write(" 开始报数人员:{0}", linkedList.CurrentItem); } Console.WriteLine(" " + "Step4:报数游戏结束"); Console.WriteLine("出队人员顺序:{0}", result + linkedList.CurrentItem); }
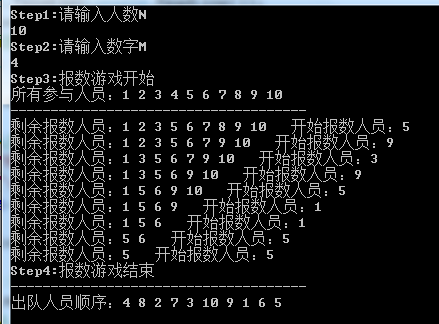
运行结果下图所示:
①N=10,M=4时:
②N=41,M=3时:
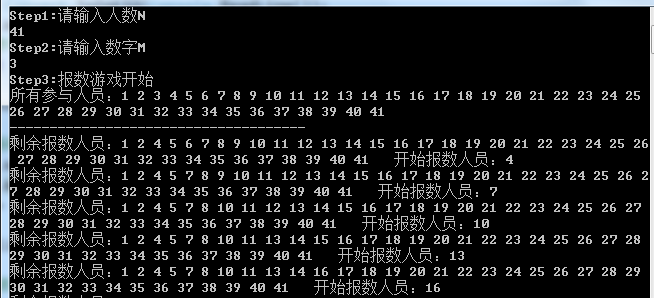

从上图结果的出队人员顺序也可以看出,约瑟夫将自己和朋友安排在第16和第31个位置是在最后出队的,就只剩他俩好基友了,死不死就不是犹太人说了算了,又可以风骚地在一起“搞基”了。
3.3 使用LinkedList<T>解决约瑟夫问题
在实际应用中,我们一般都会使用.NET中自带的数据结构类型来解决一般问题,这里我们就试着用LinkedList<T>来解决约瑟夫问题。
(1)定义一个Person类
public class Person { public int Id { get; set; } public string Name { get; set; } }
(2)初始化LinkedList集合
static LinkedList<Person> InitPersonList(int count) { LinkedList<Person> personList = new LinkedList<Person>(); for (int i = 1; i <= count; i++) { Person person = new Person(); person.Id = i; person.Name = "Counter-" + i.ToString(); personList.AddLast(person); } return personList; }
(3)由于LinkedList是双向链表,但不是循环链表,因此这里需要做一下判断
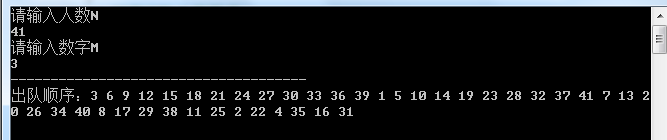
static void JosephusTestWithLinkedList() { Console.WriteLine("请输入人数N"); int n = Convert.ToInt32(Console.ReadLine()); Console.WriteLine("请输入数字M"); int m = Convert.ToInt32(Console.ReadLine()); Console.WriteLine("-------------------------------------"); LinkedList<Person> linkedList = InitPersonList(n); LinkedListNode<Person> startNode = linkedList.First; LinkedListNode<Person> removeNode; while(linkedList.Count >= 1) { for (int i = 1; i < m; i++) { if (startNode != linkedList.Last) { startNode = startNode.Next; } else { startNode = linkedList.First; } } // 记录出队人员节点 removeNode = startNode; // 打印出队人员ID号 Console.Write(removeNode.Value.Id + " "); // 确定下一个开始报数人员 if (startNode == linkedList.Last) { startNode = linkedList.First; } else { startNode = startNode.Next; } // 移除出队人员节点 linkedList.Remove(removeNode); } Console.WriteLine(); }
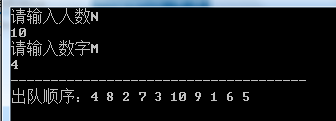
这里使用startNode记录开始报数的人员节点,removeNode则记录要出队的人员节点。这里在确定下一个开始报数人员时通过手动判断LinkedList的当前节点是否已经达到了尾节点,如果是则转到头结点进行报数。最后将removeNode从LinkedList中移除即可。最终的运行结果如下图所示:
①N=10,M=4时:
②N=41,M=3时:
PS:解决问题的思路和实现多种多样,这里给出的仅仅是最最普通的一种。
参考资料
(1)程杰,《大话数据结构》
(2)陈广,《数据结构(C#语言描述)》
(3)段恩泽,《数据结构(C#语言版)》
