自适应线性元件20世纪50年代末由Widrow和Hoff提出,主要用于线性逼近一个函数式而进行模式联想以及信号滤波、预测、模型识别和控制等。
线性神经网络和感知器的区别是,感知器只能输出两种可能的值,而线性神经网络的输出可以取任意值。线性神经网络采用Widrow-Hoff学习规则,即LMS(Least Mean Square)算法来调整网络的权值和偏置。
只能解决线性可分的问题。
与感知器类似,神经元传输函数不同。
二、LMS学习算法
Widrow和Hoff在1960年提出自适应滤波LMS算法,也称为Δ规则(Delta Rule)。LMS算法只能训练单层网络,
定义某次迭代时的信号为 e(n)=d(n)-xT(n)w(n)
其中n表示迭代次数,d表示期望输出。这里采用均方误差作为评价指标:
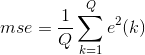
Q是输入训练样本的个数。线性神经网络学习的目标是找到适当的w,使得均方差mse最小。mse对w求偏导,令偏导等于0求得mse极值,因为mse 必为正,二次函数凹向上,求得的极值必为极小值。
实际运算中,为了解决权值w维数过高,给计算带来困难,往往调节权值,使mse从空间中的某一点开始,沿着斜面向下滑行,最终达到最小值。滑行的方向使该店最陡下降的方向,即负梯度方向。
实际计算中,代价函数常定义为
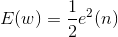
推导,梯度下降法。(推导有些复杂,可查阅书籍文献)
LMS算法步骤:与上节感知器类似。
(1)定义参数和变量。
(2)初始化
(3)输入样本,计算实际输出和误差。
(4)调整权值向量
(5)判断是否收敛
学习率的选择:
1996年Hayjin证明,只要学习率η满足 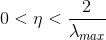 LMS算法就是按方差收敛的。
LMS算法就是按方差收敛的。
其中,λmax是输入向量x(n)组成的自相关矩阵R的最大特征值。往往使用R的迹(trace)来代替。矩阵的迹是矩阵主对角线元素之和。
可改写成 0<η<2/向量均方值之和。
学习率逐渐下降:
学习初期,用比较大的学习率保证收敛速度,随着迭代次数增加,减小学习率保证精度,确保收敛。
五、线性神经网络相关函数
newlind--设计一个线性层
net=newlind(P,T,Pi)
相当于生成了神经网络和训练了神经网络,不用再训练。
newlin--构造一个线性层
相当于生成神经网络,再更高的版本中废弃,推荐使用的新函数是linearlayer.
minmax(P) 求最大最小值。
maxlinlr(P)求最大学习率。见上节。
之后再用train训练。
purelin--线性传输函数。 输出等于输入。
learnwh--LMS学习函数