
壹 ❀ 引
做题做题,再忙每天都要抽空做一道题!今天来做一道有趣的题,题目来自多数元素,题目描述如下:
给定一个大小为 n 的数组,找到其中的多数元素。多数元素是指在数组中出现次数大于 ⌊ n/2 ⌋ 的元素。
你可以假设数组是非空的,并且给定的数组总是存在多数元素。
示例 1:
输入: [3,2,3] 输出: 3示例 2:
输入: [2,2,1,1,1,2,2] 输出: 2
我们来简单的分析下题目,看看有几种做法实现它。
贰 ❀ 题解分析
在做题之前,我们先来简单科普一个数学名词众数,所谓众数其实就是在一堆数据中出现最多次的数。当然,特殊情况下一个数组会有众数也是合理的,一般用M表示众数。
[1,1,1,2,3]//众数为1
[1,1,2,2,3]//众数为1,2
[1,2,3,4]//没有峰值,无众数
而题目要求是找出现次数大于n/2的数,其实说到底,就是也算一种特殊的众数,而且这个众数一定只有一个。为啥这么说呢,因为出现次数都已经大于所有数个数的一半了(M>n/2),剩下的数怎么都不可能比这个众数更多,或者与之一样多,比如:
[1,1,1,2,3]//1为众数,2与3已经没机会与1平起平坐,或者超越1了
[1,1,2,2,3]//没有一个数超过n/2,所以没有
所以对于这道题来说,一定只有只有一个数是最多的,我们只需要找到这个出现次数最多的数即可,怎么做呢?
贰 ❀ 壹 桶排序
我一开始想的就是桶排序,找出数组中最大的数,然后建立(max+1)个桶,为啥要加1,因为数组索引是从0开始的,如果最大的数是3,new Array(3)之后,最大的索引其实是2,那么数字3找不到对应的桶,说干就干:
/**
* @param {number[]} nums
* @return {number}
*/
var majorityElement = function (nums) {
// 找出最大数
let max = Math.max(...nums);
let backet = new Array(max + 1).fill(0);
nums.forEach(item => {
// 将对应桶的数递增
backet[item]++;
});
// 找到数字最大的那个桶,也就是我们想要的数了
return backet.findIndex(item => item > nums.length / 2);
};
这个实现在本地跑是可以的,但是提交了就报错,错误理由leetcode也给不出来,反正我也挺莫名其妙的。
贰 ❀ 贰 字典
这个实现显然是不太优化的,打个比方,假设不凑巧的是[9999,9999,1],那我们就得建立9999个桶,也就是说数字范围给的越大,咱们最后遍历桶耗时也就越久,有没有更棒的做法呢?其实我们可以使用哈希表或者字典直接来统计每个数字出现的次数,这里我用字典来做:
/**
* @param {number[]} nums
* @return {number}
*/
var majorityElement = function (nums) {
// 建立一个字典
let dic = {};
nums.forEach(item => {
// 将数字作为key,出现次数作为value,每出现一次自增1
dic[item] = dic[item] || 0;
dic[item]++;
});
// 找到value最大的key返回即可
return Object.keys(dic).find(item => {
return dic[item] > nums.length / 2;
});
};
贰 ❀ 叁 排序
还有没有更直接的办法呢?其实这里就需要动下脑筋了。我们在前面说,本题是找出出现次数比n/2还要多的数,且这个数只有一个。如果我们将数组进行排序,会发生什么呢?
我们简单脑补一下,假设数组n为偶数,比如一共4个,那么这个众数起码得有3个;假设是奇数,比如5个,那么这个数也起码得有3个,看个图:

不管奇数偶数,取中间一位的数就是我们要找的数,有同学就说了,不对啊,偶数除不断,那就取中间数,不能整除就向下取整:
/**
* @param {number[]} nums
* @return {number}
*/
var majorityElement = function (nums) {
nums.sort((a, b) => a - b);
return nums[Math.floor(nums.length/2)];
};
有同学就要问了,为啥不能向上取整,看图片上取整好像也可以,这是因为我们还得考虑只有一个元素的情况,比如[1],1/2=0.5,1次比0.5要大,所以也满足,如果用ceil那就取到undefined了。
贰 ❀ 肆 摩尔投票法
首先,什么是摩尔投票法呢?这里引用知乎用户的解释,原答案地址

啥意思?由于我们已知数组中一定有这个最多的数,且数量超过数组长度一般,我们把每个数比喻成一个国家,数字出现频率表示这个国家有多少人,现在发动战争,以一个人消耗一个人来看,最后剩下的人一定是最多国家的人。
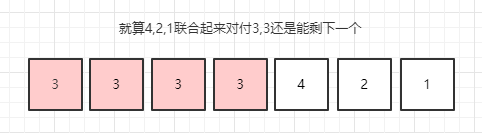
有同学可能就想要数字出现顺序的问题,虽然你多,但是如果大家都打你,都消耗你怎么办?没关系,前面已经说了,这个国家人数超过了总人数一半,就算你们一起联合起来消耗我,我还是能有剩下的人,那么这个剩下的人就是最多的数了。
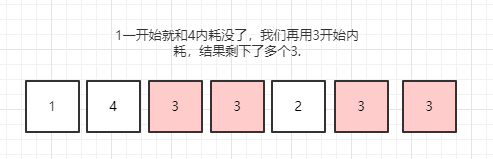
有同学又要问了,那假设一开始这个数,不是最多的那个那个,直接被消耗完了咋办?没关系,我们可以假定第一个数表示最多,然后开始内耗,只要内耗变成了0,我们就将下一位数认定为最多,继续开始内耗,运气不好,就是最多的数和所有的其它数打架。运气好就是其它数内耗的差不多了,最多的数能剩下不止一个。所以不管怎么说,我们总是能找到最多的那个数:
/**
* @param {number[]} nums
* @return {number}
*/
var majorityElement = function (nums) {
// 假设第一个数是最多的数
let num = nums[0],
// 默认参战人数是1
count = 1;
for (let i = 1; i < nums.length; i++) {
// 开始打仗,相同是自己人,加1
if (num == nums[i])
count++;
else {
// 反之内耗掉,判断变成0没有,变了就取下一位成为假定最多的那个
count--;
if (count == 0) {
num = nums[i + 1];
};
};
};
return num;
};
那么到这里,本文结束。