壹 ❀ 引
今天做的一题是前两周博客园一粉丝在面试360时遇到的算法题,题目来自leetcode88. 合并两个有序数组,理解起来可能有些费劲,不过我尽量用图的形式给大家解释它,题目描述如下:
给你两个有序整数数组
nums1和nums2,请你将nums2合并到nums1中,使nums1成为一个有序数组。说明:
初始化
nums1和nums2的元素数量分别为 m 和 n 。
你可以假设nums1有足够的空间(空间大小大于或等于 m + n)来保存nums2中的元素。示例:
输入: nums1 = [1,2,3,0,0,0], m = 3 nums2 = [2,5,6], n = 3 输出: [1,2,2,3,5,6]
我们先来简单分析题目,再来看看如何解决它。
贰 ❀ 题解分析
首先,数组nums1与nums2都是有序数组,有些奇怪的是,nums1中的剩余空间都是以0表示,而这些位置就是为nums2准备的,我们要做的就是将nums2放进nums1中,当然,我们还得保证合并之后nums1的有序性。
由于题目不需要return新数组,而是在原数组nums1上做修改,所以我第一想到的暴力做法就是将nums1中的0全部裁剪掉,并将nums2加入进去,再做排序,那么这里就可以使用splice方法,略微暴力的做法:
/**
* @param {number[]} nums1
* @param {number} m
* @param {number[]} nums2
* @param {number} n
* @return {void} Do not return anything, modify nums1 in-place instead.
*/
var merge = function (nums1, m, nums2, n) {
// 从m位开始裁剪n个元素后,并将nums2的元素加入进去
nums1.splice(m, n, ...nums2)
// 重排nums1
nums1.sort((a, b) => a - b);
};
这样能解决问题,不过有些违背题目本意,数组的有序性我们并未利用,确实有些投机取巧了。而且在360面试中,该粉丝也被问到双指针优化问题,比较巧的是官方推荐做法也是双指针,所以我们还是站在双指针角度来重新看待这个问题。
由于nums1中的0其实就是预留给nums2的空间,准确来说,我们要做的就是将0替换成nums1或nums2的元素,这个据排序大小而定。
m和n分别代表了nums1与nums2的有效元素个数,因此合并完成后的新nums1长度为m+n-1。
由于数组nums1与nums2都是有序数组,所以不难想要,如果num2中的一个元素比nums1的最后一个元素大,那么一定比nums1的其它元素都大,这样相比正序比较,倒序遍历耗时会大大减少。
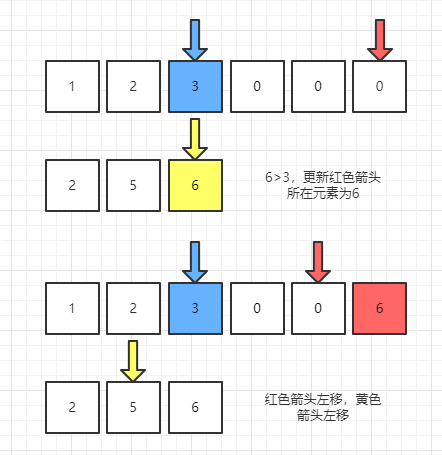
我们先来看一张过程图,再来解释做了什么:
第一次比较
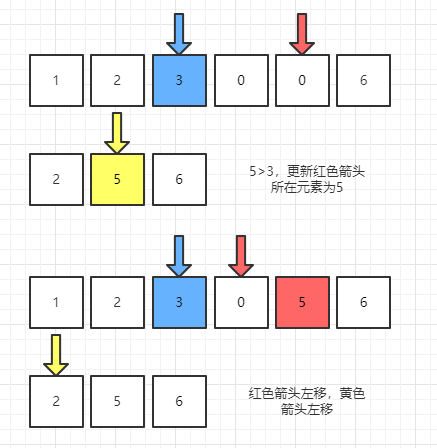
第二次比较
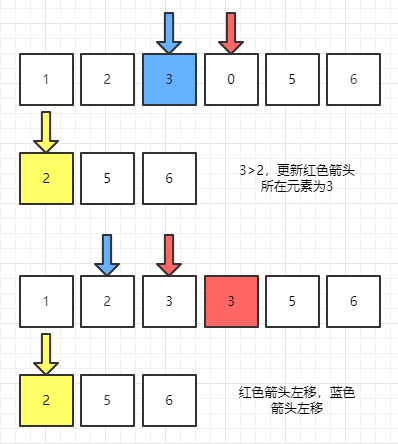
第三次比较
第四次比较
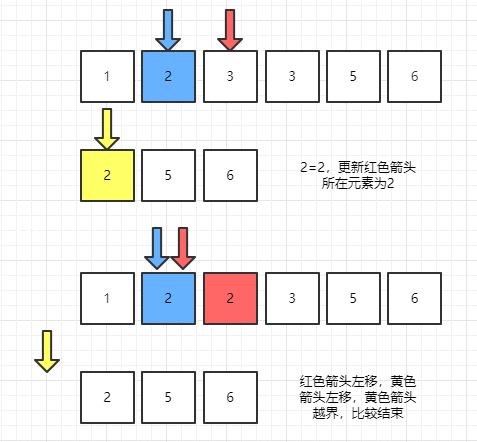
那么我们现在要对nums1倒序更新元素,同时需要两个指针,分别指向nums1的m-1处与nums2的n-1处,然后开始比较,如果nums2的最后一个元素比nums1的最后一个元素大(注意,这里的最后是m-1),那么nums1索引为m+n-1处的0就应该被替换成nums2的最后一个元素,为啥呢,首先数组都是有序的,nums2的最后一个元素相对自己是最大的一个数,如果它比nums1的最后一个元素大,自然也会比前面其它所有数都大,放到最后是毋庸置疑的。
在经过这次比较后,因为nums2最后一个元素已经被使用了,所以nums2的指针左移,进行下次比较。如果遇到nums1的元素比nums2大的情况,我们还是一样的将nums1的元素添加到后面,同理nums1的指针要开始左移。
其实不难想象,一共有三个指针,指针p1(指针的单词是pointer)与p2分别指向nums1与nums2的有效元素位,指针p指向nums1的最后一位,经过比较,我们使用将较大的放到nums1的p位,此时p就得左移,p做的工作就是负责不断的替换nums1中的元素。
我觉得我也是够啰嗦,思路说清楚了,我们来实现它:
/**
* @param {number[]} nums1
* @param {number} m
* @param {number[]} nums2
* @param {number} n
* @return {void} Do not return anything, modify nums1 in-place instead.
*/
var merge = function(nums1, m, nums2, n) {
// p初始指向nums1最后一位
let p = m + n - 1,
p1 = m - 1,
p2 = n - 1;
//如果其中有小于0,说明直接是空数组,不用比较直接裁剪
if (p1 < 0 || p2 < 0) {
nums1.splice(0, n, ...nums2);
};
while (p2 >= 0) {
// 如果p1比p2大
if (nums1[p1] > nums2[p2]) {
// 将p1的值丢到p位置
nums1[p] = nums1[p1];
// p与p1都左移
p--;
p1--
} else {
// 反之把p2的值丢到p位置
nums1[p] = nums2[p2];
// p和p2左移
p--;
p2--
};
};
};
这段代码其实有些极限,比如当例子是[2,0],1,[1],1时,由于第一次比较2>1所以经过修改nums1变成了[2,2],紧接着p与p1递减。由于条件p2还是0满足条件,所以继续了第二次比较,而此时p1变成了负一,nums[-1]>nums2[p2]比较肯定失败,这才走了else分支,于是将nums2的1复制到了p位置,sums1变成了[1,2]。
到这里问题就凸显出来了,索引越界情况没考虑,所以正确的做法其实是这样,这里参考灵魂画手解题思路:
/**
* @param {number[]} nums1
* @param {number} m
* @param {number[]} nums2
* @param {number} n
* @return {void} Do not return anything, modify nums1 in-place instead.
*/
var merge = function(nums1, m, nums2, n) {
let len1 = m - 1;
let len2 = n - 1;
let len = m + n - 1;
while(len1 >= 0 && len2 >= 0) {
// 注意--符号在后面,表示先进行计算再减1,这种缩写缩短了代码
nums1[len--] = nums1[len1] > nums2[len2] ? nums1[len1--] : nums2[len2--];
}
function arrayCopy(src, srcIndex, dest, destIndex, length) {
dest.splice(destIndex, length, ...src.slice(srcIndex, srcIndex + length));
}
// 表示将nums2数组从下标0位置开始,拷贝到nums1数组中,从下标0位置开始,长度为len2+1
arrayCopy(nums2, 0, nums1, 0, len2 + 1);
};
这里的arrayCopy其实做了两件事,第一假设两个指针一开始有一个不满足大于等于0情况,while跳过直接裁剪,与我之前想法一样。
第二是考虑了p1越界情况,只要p1小于0,说明p1所有元素都找到了对应位置,由于全程都是在进行双指针元素比较,即使nums2还有元素没安排,那也一定是最小的几个元素,又因为nums2是有序的,所以直接裁剪过去就好了。
为什么不考虑p2越界情况呢?因为p2越界,说明nums2中所有元素都在nums1中找到了何时的位置了,同理nums1也是有序的,即使剩下的元素没比较完,那也是有序的了!
还有,while循环中的赋值与递减确实让我眼前一亮....代码实现也比我逻辑性更强,加油吧,那么本文就到这里了。