简介
对什么蚁群算法啦,遗传算法啦...... 很感兴趣,遂学习一波
遗传算法真的是一个美妙的东西,大自然最根本的力量就是进化,淘汰弱者,让强者生存。
参考文章 核心链接 链接 https://www.zhihu.com/search?q=遗传算法&utm_content=search_history&type=content
参考文章附带的代码 https://github.com/yanshengjia/artificial-intelligence/blob/master/genetic-algorithm-for-functional-maximum-problem/matlab-ga
开始个人理解
首先 个人用python 重写了 matlab
目标函数
求解函数 f(x) = x + 10*sin(5*x) + 7*cos(4*x) 在区间[0,9]的最大值
先来看看 目标函数的的校验吧 看看 在 0 - 9的区间上的值分布
测试代码
def testTarget(self):
plt.figure(1)
x = np.linspace(0, 9, 10000)
x = x.astype('float')
y = []
for i in range(len(x)):
y.append(self.targetFun(x[i]))
print(x)
print(y)
plt.plot(x, y)
plt.show()
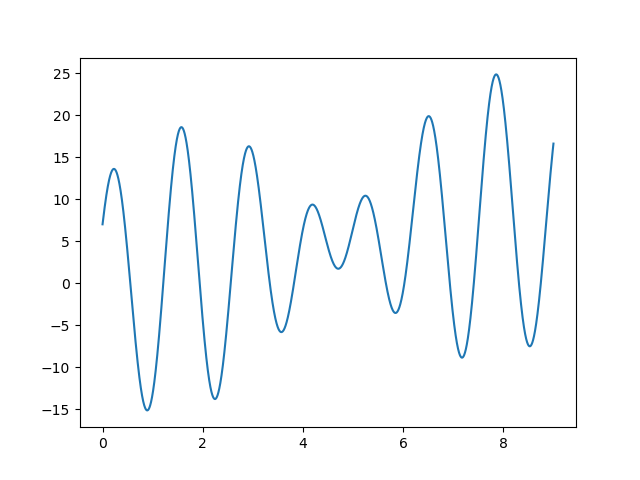
result
可以看出在8附近达到最大值为25
如果我遗传算法最后的结果在这个区间内的话,那么就可以说是正确答案
codeResult
总共迭代了1000次,种群的大小是1000个基因
最佳个体 10101111011111011
最优适应度 24.855362812666666
最优个体对应自变量值 7.856726507007652
最优个体的迭代次数 11
计算耗时 81 s
算法流程
code流
gaAlgorithm = ga.GeneticAlgorithm()
# 初始化种群 随机赋值 0110值
gaAlgorithm.initPopulation()
# debug
gaAlgorithm.debug('population')
maxGN = gaAlgorithm.getMaxNumberIteration()
start = time.process_time()
for i in range(maxGN):
# 计算适应度函数
gaAlgorithm.fitness()
# gaAlgorithm.debug('fitnessValue')
gaAlgorithm.rank()
# gaAlgorithm.debug('rank')
gaAlgorithm.selection()
# gaAlgorithm.debug('population')
gaAlgorithm.crossOver()
gaAlgorithm.mutation()
if (i % 10 == 0):
print(i, end=' ')
elapsed = (time.process_time() - start)
print("Time used:",elapsed)
gaAlgorithm.plotGA()
bestFitness, bestGeneration, bestIndividual = gaAlgorithm.getBestThreeAttr()
流程图
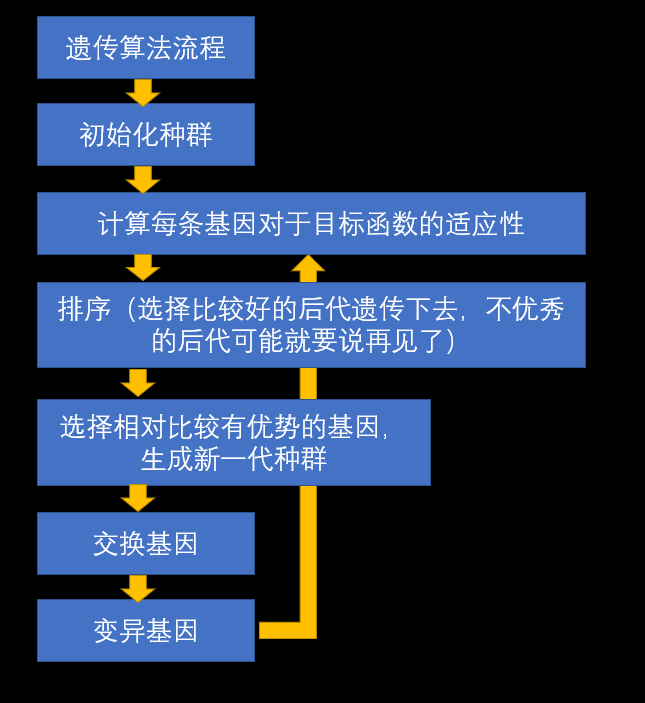
每个流程详解
计算每个基因对于目标函数的适应性
def fitness(self):
'''适应度函数'''
self.fitnessValue = []
for i in range(self.populationSize):
self.fitnessValue.append(0)
# 先存储字符串转换出来的十进制的值, 然后带入目标函数中计算出真实的值
for i in range(self.populationSize):
for j in range(self.chromosomeLength):
if (self.population[i][j] == "1"):
# print(self.population[i][j])
self.fitnessValue[i] = self.fitnessValue[i] + 2**(j)
self.fitnessValue[i] = self.lowerBound + self.fitnessValue[i] * (self.upperBound - self.lowerBound) / (2**self.chromosomeLength - 1)
# print('十进制值', self.fitnessValue[i])
self.fitnessValue[i] = self.targetFun(self.fitnessValue[i]) # 因为这个直接调用了函数所以,求函数的最大值其实就是求适应值
# print('函数值', self.fitnessValue[i])
说人话
将字符串基因转为 10进制数 然后求解目标函数 如果你求得是最大值(大部分为正数),那么适应度函数就是 转为10进制后的值 带入目标函数求得值
排序
def rank(self):
'''
对个体的适应度大小进行排序,并保留最佳个体
'''
for i in range(self.populationSize):
self.fitnessSum.append(0.)
for i in range(self.populationSize):
minIndex = i
for j in range(i, self.populationSize):
if (self.fitnessValue[j] < self.fitnessValue[minIndex]):
minIndex = j
if (minIndex != i):
tmp = self.fitnessValue[i]
self.fitnessValue[i] = self.fitnessValue[minIndex]
self.fitnessValue[minIndex] = tmp
tmpChromosome = self.population[i]
self.population[i] = self.population[minIndex]
self.population[minIndex] = tmpChromosome
for i in range(self.populationSize):
if i == 0:
self.fitnessSum[i] = self.fitnessSum[i] + self.fitnessValue[i]
else:
self.fitnessSum[i] = self.fitnessSum[i-1] + self.fitnessValue[i]
self.fitnessAverage.append(self.fitnessSum[self.populationSize - 1] / self.populationSize)
if(self.fitnessValue[self.populationSize - 1] > self.bestFitness):
self.bestFitness = self.fitnessValue[self.populationSize - 1]
self.bestGen = len(self.fitnessAverage)
self.bestIndividual = self.population[self.populationSize - 1]
说人话
根据所有的基因的适应度,然后从小到大排序。最后一个个体是最优秀的个人(King)
选择个体
def selection(self):
'''
轮盘赌选择操作,按照[0, 总适应度] 先求出结果这个是要改的 应为 这个放弃了 适应度为负的值
'''
self.populationNew = [None] * self.populationSize
for i in range(self.populationSize):
r = random.random() * self.fitnessSum[self.populationSize - 1]
first = 0
last = self.populationSize - 1
mid = round((last + first) / 2)
idx = -1
# 原文是排序选择和 r 差不多的个体(排中法?)
while(first <= last and idx==-1):
if(r > self.fitnessSum[mid]):
first = mid
elif( r < self.fitnessSum[mid]):
last = mid
else:
idx = mid # 一般不会走到这个分支因为是浮点数
break
mid = round((last + first) / 2)
if(last - first == 1):
idx = last
break
# 产生新一代的个体
self.populationNew[i] = self.population[idx]
if self.chooseElite:
p = self.populationSize - 1
else:
p = self.populationSize
for i in range(p):
self.population[i] = self.populationNew[i]
说人话
有些优势基因会重复,因为放弃了(适应值为负的基因),如果开启了优势选择,那么最优秀的个体将会直接出现在新种群(待交叉配对列表) King~
交叉
def crossOver(self):
'''
交叉 改进 交换前一半的基因 = 交换后一半的基因
'''
for i in range(0, self.populationSize, 2):
# 生成随机概率
if (random.random() < self.crossoverProbability):
crossPosition = round(random.random() * self.chromosomeLength)
if (crossPosition == 0) or (crossPosition == 1):
continue
# 对crossPosition及之后的二进制串进行交换
tmp = self.population[i][crossPosition:]
self.population[i] = self.population[i][0:crossPosition] + self.population[i+1][crossPosition:]
self.population[i+1] = self.population[i+1][0:crossPosition] + tmp
说人话
虽然生成了待交叉的列表,但不是每对个体都会进行交叉,如果不交叉,那么他们就会自己流传下来,如果发生了交叉,那么就和他的配对对象交换基因。
变异
def mutation(self):
'''
单点变异操作
'''
for i in range(self.populationSize):
if (random.random() < self.mutationProbability):
mutationPosition = round(random.random() * self.chromosomeLength)
if mutationPosition == self.chromosomeLength:
continue
tmp = list(self.population[i])
if ( tmp[mutationPosition] == '1'):
tmp[mutationPosition] = '0'
else:
tmp[mutationPosition] = '1'
self.population[i] = ''.join(tmp)
说人话
对于每一条基因,其中的某一个一个序列点 会发生翻转。
code
https://github.com/lishaohsuai/algorithm
自问自答环节
什么是 轮盘赌算法
就是每个基因的适应度值放在一个圆盘上,依据其占有的面积(适应度值)放在轮盘上,如果生成一个随机数,如果他落在这个轮盘的一个盘面上,这个小扇形代表的基因就被选中,也就是说,适应度值越高的越有可能被选中。
如果没有被选中怎么办?恭喜你可以领盒饭了,你的基因序列被自然界丢弃。
下一步
现在迭代 1000 个种群,1000次迭代花费了 81s , 下一步改写成 numpy 版本,争取 2s 内完成1000个种群的迭代,另外适应度函数有点问题,逻辑上来说,适应度函数的值不应该是负值。