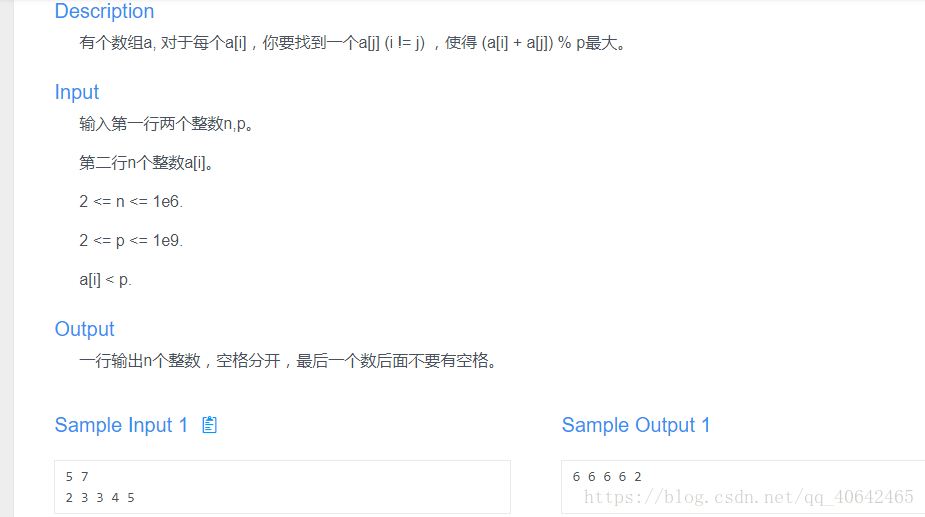
这题是贪心做的,题目要求对序列里的每个数,找另外一个数使得这2个数和的模最大,总共有2种情况1.a[i]+a[j]<p 2.a[i]+a[k]>=p 由a[i]+a[j]>=a[i]+a[k]-p ,所以在a[j]存在的时候考虑前一种情况就可以,a[j]不存在就考虑后一种情况即可。 贪心地想想 优先考虑这种情况如果a[i]+a[j]<p,而且a[j]取得最大值的情况,a[i]+a[j]不用取模p就已经是最大值了,求a[j]的最大值就利用了a[i]+a[j]<p这个不等式,可以转化为a[j]<p-a[i],要求a[j],就需要在数组里找>=p-a[i]的第一个数设为m,然后再找小于m的数里最大的那个数,这里要注意分类讨论,因为可能比m小的数不存在(这样情况就是不满足a[i]+a[j]<p的情况,那么a[i]+a[j]>=p,那么由于a[i]+a[j]<2p的,那么这2个数的模和是要减个p的所以令a[j]取得数组的最大值,这里也要注意下标相同的情况),也可能比m小的数里最大的那个数存在,但是要注意它的下标和i相同的情况。
顺便学了一下如何用lower_bound查结构体里的值
#include<bits/stdc++.h>
using namespace std;
#define inf 0x3f3f3f3f
const int maxn=1e6+10;
int a[maxn];
struct node
{
int v,id;
friend bool operator <(const node&a,const node&b)//二分查找的是结构体,需要指定比较的要素
{
return a.v<b.v;
}
}b[maxn];
bool cmp(const node&a,const node&b)
{
return a.v<b.v;
}
int main()
{
std::ios::sync_with_stdio(false);
int n,mod;
cin>>n>>mod;
for(int i=1;i<=n;i++)
{
cin>>a[i];
b[i].v=a[i];
b[i].id=i;
}
sort(b+1,b+n+1,cmp);
//cout<<"after sort:"<<endl;
//for(int i=1;i<=n;i++) cout<<b[i].v<<" "<<b[i].id<<" ***";
//cout<<endl;
for(int i=1;i<=n;i++)
{
node nod;
nod.v=mod-a[i];
nod.id=0;
int pos=lower_bound(b+1,b+n+1,nod)-b-1;//pos如果为0表示小于mod-a[i]的值不存在,否则pos表示的是小于mod-a[i]的数里最大的那一个
//cout<<"pos:"<<pos<<endl;
if(pos==0)
{
if(b[n].id!=i)
cout<<(b[n].v+a[i])%mod<<" ";
else
cout<<(b[n-1].v+a[i])%mod<<" ";
}
else
if(b[pos].id!=i)
cout<<b[pos].v+a[i]<<" ";
else
{
if(pos-1==0)
{
cout<<(b[n].v+a[i])%mod<<" ";
}
else
cout<<(b[pos-1].v+a[i])<<" ";
}
}
cout<<endl;
return 0;
}