二叉搜索树
1,定义
二叉查找树(Binary Search Tree),又名二叉搜索树或二叉排序树。可以是一颗空树,或者是具有下列性质的二叉树:
(1)若它的左子树不空,则左子树上所有结点的指均小于它的根结点的值;
(2)若它的右子树不空,则右子树上所有结点的指均大于它的根结点的值;
2,C++实现二叉树的基本操作
#include<iostream>
#include<queue>
#include<stack>
using namespace std;
/*BST树的结点类型*/
template <typename T>
struct BSTNode
{
BSTNode(T data=T()):mdata(data),mleft(NULL),mright(NULL){}//T data=T():0的初始化
T mdata;
BSTNode<T>*mleft;
BSTNode<T>*mright;
};
template<typename T>
class BSTree
{
public:
BSTree():mroot(NULL){}
~BSTree(){}
/*向BST树中插入数据:
过程为:
若b是空树,则将val所指结点作为根结点插入,否则:
若val等于b的根结点的数据域之值,则返回,否则:
若val小于b的根结点的数据域之值,则把val所指结点插入到左子树中,否则:
把val所指结点插入到右子树中
*/
void insert(const T&val)
{
if(mroot==NULL)
{
mroot=new BSTNode<T>(val);
return;
}
BSTNode<T>*ppre=mroot;
BSTNode<T>*pcur=mroot;
while(pcur!=NULL)
{
ppre=pcur;
if(val<pcur->mdata)
{
pcur=pcur->mleft;
}
else if(val>pcur->mdata)
{
pcur=pcur->mright;
}
else
{
return;
}
}
if(val<ppre->mdata)
{
ppre->mleft=new BSTNode<T>(val);
}
else
{
ppre->mright=new BSTNode<T>(val);
}
}
/*BST树的结点删除
在二叉排序树删去一个结点,分三种情况讨论:
若*p结点为叶子结点,即PL(左子树)和PR(右子树)均为空树。由于删去叶子结点不破坏整棵树的结构,则只需修改其双亲结点的指针即可。
若*p结点只有左子树PL或右子树PR,此时只要令PL或PR直接成为其双亲结点*f的左子树或右子树即可,作此修改也不破坏二叉排序树的特性。
若*p结点的左子树和右子树均不空。在删去*p之后,为保持其它元素之间的相对位置不变,可按中序遍历保持有序进行调整,可以有两种做法:其一是令*p的左子树为*f的左子树,*s为*f左子树的最右下的结点,而*p的右子树为*s的右子树;其二是令*p的直接前驱(或直接后继)替代*p,然后再从二叉排序树中删去它的直接前驱(或直接后继)。在二叉排序树上删除一个结点的算法如下:
*/
void remove(const T&val)
{
if(mroot==NULL)
{
return;
}
BSTNode<T>*ppre=NULL;
BSTNode<T>*pcur=mroot;
while(pcur!=NULL)
{
if(val<pcur->mdata)
{
pcur=pcur->mleft;
}
else if(val>pcur->mdata)
{
pcur=pcur->mright;
}
else
{
break;
}
}
if(pcur==NULL)
{
return;
}
if(pcur->mleft!=NULL&&pcur->mright!=NULL)
{
ppre=pcur;
BSTNode<T>*pdel=pcur->mleft;
ppre=pcur;
BSTNode<T>*pdel=pcur->mleft;
while(pdel->mright!=NULL)
{
ppre=pcur;
pdel=pdel->mright;
}
//pdel为待删除的结点
pcur->mdata=pdel->mdata;
pcur=pdel;
}
//开始删除结点,记录当前待删除结点的自孩子
BSTNode<T>*pchild=NULL;
if(pcur->mleft!=NULL)
{
pchild=pcur->mright;
}
else if(pcur->mright!=NULL)
{
pchild=pcur->mleft;
}
//pcur 开始删除操作
if(ppre==NULL)
{
mroot=pchild;
}
else if(pcur->mdata<=ppre->mdata)
{
ppre->mleft=pchild;
}
else
{
ppre->mright=pchild;
}
delete pcur;
}
/*BST树的查找*/
bool query(const T&val)
{
BSTNode<T>*pcur=mroot;
while(pcur!=NULL)
{
if(val<pcur->mdata)
{
pcur=pcur->mleft;
}
else if(val>pcur->mdta)
{
pcur=pcur->mright;
}
else
{
return true;
}
}
return false;
}
/*层序遍历*/
void level()
{
cout<<"层序遍历为:";
queue<BSTNode<T>*>QUE;
QUE.push(mroot);
while(!QUE.empty())
{
BSTNode<T>*pcur=QUE.front();
cout<<pcur->mdata<<" ";
if(pcur->mleft!=NULL)
{
QUE.push(pcur->mleft);
}
if(pcur->mright!=NULL)
{
QUE.push(pcur->mright);
}
QUE.pop();
}
cout<<endl;
}
/*前序遍历*/
//递归实现
void preOrder()
{
preOrder(mroot);
}
//非递归实现
void preOrder1()
{
if(mroot==NULL)
{
return;
}
cout<<"前序遍历为:";
stack<BSTNode<T>*>Stack;
BSTNode*pcur=mroot;
while(pcur!=NULL||!Stack.empty())
{
while(pcur!=NULL)
{
cout<<pcur->mdata<<" ";
Stack.push(pcur);
pcur=pcur->mleft;
}
if(!Stack.empty())
{
pcur=Stack.top();
Stack.pop()
pcur=pcur->mright;
}
}
cout<<endl;
}
/*中序遍历*/
//递归实现
void inOrder()
{
inOrder(mroot);
}
//非递归实现
void inOrder1()
{
cout<<"中序遍历为:";
if(mroot==NULL)
{
return;
}
stack<BSTNode<T>*>Stack1;
BSTNode<T>*pcur=mroot->mleft;
Stack1.push(mroot);
while(pcur!=NULL||!Stack1.empty())
{
while(pcur!=NULL)
{
Stack1.push(pcur);
pcur=pcur->mleft;
}
pcur=Stack1.top();
Stack1.pop();
cout<<pcur->mdata<<" ";
pcur=pcur->mright;
}
cout<<endl;
}
/*后序遍历*/
//递归实现
void lastOrder()
{
lastOrder(mroot);
}
//非递归实现
void lastOrder1()
{
if(mroot==NULL)
{
return;
}
cout<<"后序遍历为:";
stack<BSTNode<T>*>Stack2;
BSTNode<T>*pcur=NULL;
BSTNode<T>*pcur=mroot;
while(pcur!=NULL||!Stack2.empty())
{
while(pcur!=NULL)
{
Stack2.push(pcur);
pcur=pcur->mleft;
}
pcur=Stack2.top();
if(pcur->mright==NULL||pcur->mright=ppre)
{
cout<pcur->mdata<<" ";
ppre=pcur;
Stack2.pop();
pcur=NULL;
}
else
pcur=pcur->mright;
}
cout<<endl;
}
private:
BSTNode<T>*mroot;//指向BST树的根节点
void preOrder(BSTNode<T>*pnode)
{
if(pnode!=NULL)
{
cout<<pcur->mdata<<" ";
preOrder(pnode->mleft);
preOrder(pnode->mright);
}
}
void inOrder(BSTNode<T>*pnode1)
{
if(pnode1!=NULL)
{
cout<<pcur->mdata<<" ";
inOrder(pnode1->mleft);
inOrder(pnode1->mright);
}
}
void lastOrder(BSTNode<T>*pnode2)
{
if(pnode2!=NULL)
{
cout<<pcur->mdata<<" ";
lastOrder(pnode2->mleft);
lastOrder(pnode2->mright);
}
}
}
函数实现:
int main()
{
BSTree<int>tree;
tree.insert(57);
tree.insert(24);
tree.insert(90);
tree.insert(8);
tree.insert(35);
tree.insert(68);
tree.insert(124);
tree.insert(12);
tree.insert(46);
tree.insert(79);
tree.insert(234);
//tree.remove(35);
tree.level();
tree.preOrder1();
tree.inOrder();
tree.lastOrder();
return 0;
}
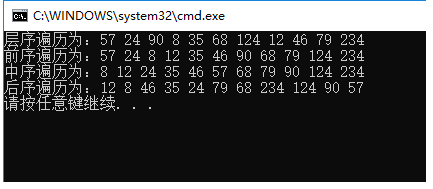
结果: