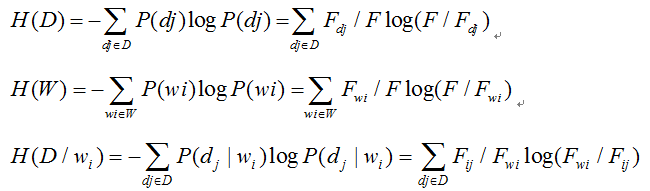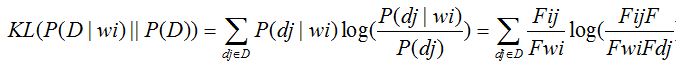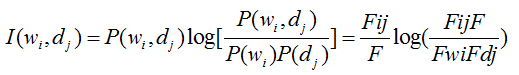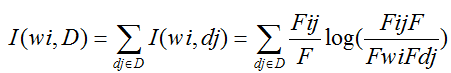从互信息的角度来理解tf-idf

先介绍tf idf

在一份给定的文件里，词频（term frequency，tf）指的是某一个给定的词语在该文件中出现的频率。这个数字是对词数（term count）的归一化，以防止它偏向长的文件。（同一个词语在长文件里可能会比短文件有更高的词数，而不管该词语重要与否。）对于在某一特定文件里的词语来说，它的重要性可表示为：

以上式子中是该词在文件中的出现次数，而分母则是在文件中所有字词的出现次数之和。

逆向文件频率（inverse document frequency，idf）是一个词语普遍重要性的度量。某一特定词语的idf，可以由总文件数目除以包含该词语之文件的数目，再将得到的商取以10为底的对数得到：

其中

• |D|：语料库中的文件总数
• ：包含词语的文件数目（即的文件数目）如果词语不在数据中，就导致分母为零，因此一般情况下使用

然后

某一特定文件内的高词语频率，以及该词语在整个文件集合中的低文件频率，可以产生出高权重的tf-idf。因此，tf-idf倾向于过滤掉常见的词语，保留重要的词语。

互信息：

一般地，两个离散随机变量 X 和 Y 的互信息可以定义为：

其中 p(x,y) 是 X 和 Y 的联合概率分布函数，而 和 分别是 X 和 Y 的边缘概率分布函数。

在连续随机变量的情形下，求和被替换成了二重定积分：

其中 p(x,y) 当前是 X 和 Y 的联合概率密度函数，而  和  分别是 X 和 Y 的边缘概率密度函数。

如果对数以 2 为基底，互信息的单位是bit。

直观上，互信息度量 X 和 Y 共享的信息：它度量知道这两个变量其中一个，对另一个不确定度减少的程度。例如，如果 X 和 Y 相互独立，则知道 X 不对 Y 提供任何信息，反之亦然，所以它们的互信息为零。在另一个极端，如果 X 是 Y 的一个确定性函数，且 Y 也是 X 的一个确定性函数，那么传递的所有信息被 X 和 Y共享：知道 X 决定 Y 的值，反之亦然。因此，在此情形互信息与 Y（或 X）单独包含的不确定度相同，称作 Y（或 X）的熵。而且，这个互信息与 X 的熵和 Y 的熵相同。（这种情形的一个非常特殊的情况是当 X 和 Y 为相同随机变量时。）

互信息是 X 和 Y 联合分布相对于假定 X 和 Y 独立情况下的联合分布之间的内在依赖性。 于是互信息以下面方式度量依赖性：I(X; Y) = 0 当且仅当 X 和 Y 为独立随机变量。从一个方向很容易看出：当 X 和 Y 独立时，p(x,y) = p(x) p(y)，因此：

此外，互信息是非负的（即 I(X;Y) ≥ 0; 见下文），而且是对称的（即 I(X;Y) = I(Y;X)）。

我们首先列出以下要用的一些变量：

D：文档随机变量D。

P（D）：D的分布。

W：词条随机变量W。

P（W）：W的分布。

P（D|W）：已知W,D的条件分布。

P（wi,dj）：提出词条wi,得到dj的概率。

F：所有文档相加的总次数。

Fij:词条i在文档j中出现的频率。

Fwi:词条wi在所有文档中的总频率。

Fdj:单个文档dj中的词数。

基于频率的概率模型：

我们假设词条wi提出的频率等于其出现的频率：

P（Wi）=Fwi/F

每个文档的出现概率与其包含词数成正比：

P（dj）=Fdj/F

提出wi以后，每个文档被取出的概率，也等于其包含wi频率比例：

P（dj|wi）=Fij/Fwi

Wi和dj同时发生的概率等于dj包含词条wi的频率：

P（wi，dj）=P(wi)*P(dj|wi)=Fwi/F*Fij/Fwi=Fij/F

H表示信息熵,I表示互信息,KL表示KL距离．

于是，再带入之前的信息论模型，得到：

熵:

KL距离:

PWI(互信息):

(1)

 

(2)

 

 

参考资料：

https://blog.csdn.net/ice110956/article/details/17243071