问题背景
给出N个集合,找到相似的集合对,如何实现呢?直观的方法是比较任意两个集合。那么可以十分精确的找到每一对相似的集合,但是时间复杂度是O(n2)。当N比较小时,比如K级,此算法可以在接受的时间范围内完成,但是如果N变大时,比B级,甚至P级,那么需要的时间是不能够被接受的。比如N= 1B = 1,000,000,000。一台计算机每秒可以比较1,000,000,000对集合是否相等。那么大概需要15年的时间才能找到所有相似的集合!
上面的算法虽然效率很低,但是结果会很精确,因为检查了每一对集合。假如,N个集合中只有少数几对集合相似,绝大多数集合都不等呢?那么根据上述算法,绝大多数检测的结果是两个结合不相似,可以说这些检测“浪费了计算时间”。所以,如果能找到一种算法,将大体上相似的集合聚到一起,缩小比对的范围,这样只用检测较少的集合对,就可以找到绝大多数相似的集合对,大幅度减少时间开销。虽然牺牲了一部分精度,但是如果能够将时间大幅度减少,这种算法还是可以接受的。接下来的内容讲解如何使用Minhash和LSH(Locality-sensitive Hashing)来实现上述目的,在相似的集合较少的情况下,可以在O(n)时间找到大部分相似的集合对。
Jaccard相似度
判断两个集合是否相等,一般使用称之为Jaccard相似度的算法(后面用Jac(S1,S2)来表示集合S1和S2的Jaccard相似度)。举个列子,集合X = {a,b,c},Y = {b,c,d}。那么Jac(X,Y) = 2 / 3 = 0.67。也就是说,结合X和Y有67%的元素相同。下面是形式的表述Jaccard相似度公式:
Jac(X,Y) = |X∩Y| / |X∪Y|
也就是两个结合交集的个数比上两个集合并集的个数。范围在[0,1]之间。
降维技术Minhash
原始问题的关键在于计算时间太长。所以,如果能够找到一种很好的方法将原始集合压缩成更小的集合,而且又不失去相似性,那么可以缩短计算时间。Minhash可以帮助我们解决这个问题。举个例子,S1 = {a,d,e},S2 = {c, e},设全集U = {a,b,c,d,e}。集合可以如下表示:
|
行号 |
元素 |
S1 |
S2 |
类别 |
|
1 |
a |
1 |
0 |
Y |
|
2 |
b |
0 |
0 |
Z |
|
3 |
c |
0 |
1 |
Y |
|
4 |
d |
1 |
0 |
Y |
|
5 |
e |
1 |
1 |
X |
表1
表1中,列表示集合,行表示元素,值1表示某个集合具有某个值,0则相反(X,Y,Z的意义后面讨论)。Minhash算法大体思路是:采用一种hash函数,将元素的位置均匀打乱,然后将新顺序下每个集合第一个元素作为该集合的特征值。比如哈希函数h1(i) = (i + 1) % 5,其中i为行号。作用于集合S1和S2,得到如下结果:
|
行号 |
元素 |
S1 |
S2 |
类别 |
|
1 |
e |
1 |
1 |
X |
|
2 |
a |
1 |
0 |
Y |
|
3 |
b |
0 |
0 |
Z |
|
4 |
c |
0 |
1 |
Y |
|
5 |
d |
1 |
0 |
Y |
|
Minhash |
e |
e |
||
表2
这时,Minhash(S1) = e,Minhash(S2) = e。也就是说用元素e表示S1,用元素e表示集合S2。那么这样做是否科学呢?进一步,如果Minhash(S1) 等于Minhash(S2),那么S1是否和S2类似呢?
一个神奇的结论
P(Minhash(S1) = Minhash(S2)) = Jac(S1,S2)
在哈希函数h1均匀分布的情况下,集合S1的Minhash值和集合S2的Minhash值相等的概率等于集合S1与集合S2的Jaccard相似度,下面简单分析一下这个结论。
S1和S2的每一行元素可以分为三类:
l X类 均为1。比如表2中的第1行,两个集合都有元素e。
l Y类 一个为1,另一个为0。比如表2中的第2行,表明S1有元素a,而S2没有。
l Z类 均为0。比如表2中的第3行,两个集合都没有元素b。
这里忽略所有Z类的行,因为此类行对两个集合是否相似没有任何贡献。由于哈希函数将原始行号均匀分布到新的行号,这样可以认为在新的行号排列下,任意一行出现X类的情况的概率为|X|/(|X|+|Y|)。这里为了方便,将任意位置设为第一个出现X类行的行号。所以P(第一个出现X类) = |X|/(|X|+|Y|) = Jac(S1,S2)。这里很重要的一点就是要保证哈希函数可以将数值均匀分布,尽量减少冲撞。
一般而言,会找出一系列的哈希函数,比如h个(h << |U|),为每一个集合计算h次Minhash值,然后用h个Minhash值组成一个摘要来表示当前集合(注意Minhash的值的位置需要保持一致)。举个列子,还是基于上面的例子,现在又有一个哈希函数h2(i) = (i -1)% 5。那么得到如下集合:
|
行号 |
元素 |
S1 |
S2 |
类别 |
|
1 |
b |
0 |
0 |
Z |
|
2 |
c |
0 |
1 |
Y |
|
3 |
d |
1 |
0 |
Y |
|
4 |
e |
1 |
1 |
X |
|
5 |
a |
1 |
0 |
Y |
|
Minhash |
d |
c |
||
表3
所以,现在用摘要表示的原始集合如下:
|
哈希函数 |
S1 |
S2 |
|
h1(i) = (i + 1) % 5 |
e |
e |
|
h2(i) = (i - 1) % 5 |
d |
c |
表4
从表四还可以得到一个结论,令X表示Minhash摘要后的集合对应行相等的次数(比如表4,X=1,因为哈希函数h1情况下,两个集合的minhash相等,h2不等):
X ~ B(h,Jac(S1,S2))
X符合次数为h,概率为Jac(S1,S2)的二项分布。那么期望E(X) = h * Jac(S1,S2) = 2 * 2 / 3 = 1.33。也就是每2个hash计算Minhash摘要,可以期望有1.33元素对应相等。
所以,Minhash在压缩原始集合的情况下,保证了集合的相似度没有被破坏。
LSH – 局部敏感哈希
现在有了原始集合的摘要,但是还是没有解决最初的问题,仍然需要遍历所有的集合对,,才能所有相似的集合对,复杂度仍然是O(n2)。所以,接下来描述解决这个问题的核心思想LSH。其基本思路是将相似的集合聚集到一起,减小查找范围,避免比较不相似的集合。仍然是从例子开始,现在有5个集合,计算出对应的Minhash摘要,如下:
|
S1 |
S2 |
S3 |
S4 |
S5 |
|
|
区间1 |
b |
b |
a |
b |
a |
|
c |
c |
a |
c |
b |
|
|
d |
b |
a |
d |
c |
|
|
区间2 |
a |
e |
b |
e |
d |
|
b |
d |
c |
f |
e |
|
|
e |
a |
d |
g |
a |
|
|
区间3 |
d |
c |
a |
h |
b |
|
a |
a |
b |
b |
a |
|
|
d |
e |
a |
b |
e |
|
|
区间4 |
d |
a |
a |
c |
b |
|
b |
a |
c |
b |
a |
|
|
d |
e |
a |
b |
e |
表5
上面的集合摘要采用了12个不同的hash函数计算出来,然后分成了B = 4个区间。前面已经分析过,任意两个集合(S1,S2)对应的Minhash值相等的概率r = Jac(S1,S2)。先分析区间1,在这个区间内,P(集合S1等于集合S2) = r3。所以只要S1和S2的Jaccard相似度越高,在区间1内越有可能完成全一致,反过来也一样。那么P(集合S1不等于集合S2) = 1 - r3。现在有4个区间,其他区间与第一个相同,所以P(4个区间上,集合S1都不等于集合S2) = (1 – r3)4。P(4个区间上,至少有一个区间,集合S1等于集合S2) = 1 - (1 – r3)4。这里的概率是一个r的函数,形状犹如一个S型,如下:
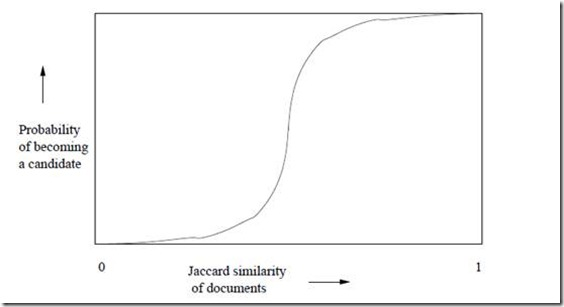
图1
如果令区间个数为B,每个区间内的行数为C,那么上面的公式可以形式的表示为:
P(B个区间中至少有一个区间中两个结合相等) = 1 - (1 – rC)B
领r = 0.4,C=3,B = 100。上述公式计算的概率为0.9986585。这表明两个Jaccard相似度为0.4的集合在至少一个区间内冲撞的概率达到了99.9%。根据这一事实,我们只需要选取合适的B和C,和一个冲撞率很低的hash函数,就可以将相似的集合至少在一个区间内冲撞,这样也就达成了本节最开始的目的:将相似的集合放到一起。具体的方法是为B个区间,准备B个hash表,和区间编号一一对应,然后用hash函数将每个区间的部分集合映射到对应hash表里。最后遍历所有的hash表,将冲撞的集合作为候选对象进行比较,找出相识的集合对。整个过程是采用O(n)的时间复杂度,因为B和C均是常量。由于聚到一起的集合相比于整体比较少,所以在这小范围内互相比较的时间开销也可以计算为常量,那么总体的计算时间也是O(n)。
总结
以上只是描述了Minhash和LSH寻找相似集合的算法框架,作为学习笔记和备忘录。还有一些算法细节没有讨论。希望后面有机会,可以在海量数据的情况下使用这个算法。