图算法 单源最短路径 Bellman_Ford算法（边权值为负情况）

一、前瞻

　　在之前的单源最短路径Dijkstra算法中，博主给出了最短路径的一些基本概念和问题，并且给出了对权值不能为负的图使用Dijkstra算法求解单源最短路径问题的方法。

　　我们提到，Dijkstra算法的一个巨大前提是：不能有权值为负的边。因为当权值可以为负时，可能在图中会存在负权回路，最短路径只要无限次地走这个负权回路，便可以无限制地减少它的最短路径权值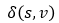，这就变相地说明最短路径不存在，Dijkstra算法无法终止。下图说明从u到v的最短路径是不存在的。

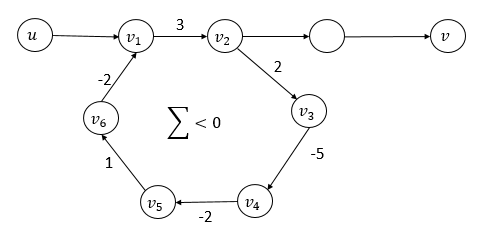
　　那么，应该用什么方法求解？

　　上面我们说Dijkstra算法无法终止，我们可能会想，可不可以试图让Dijkstra算法终止呢？

　　当Dijkstra算法运行时，突然找到了一个负权回路，这下糟糕做不下去了，那么赶快终止算法跳出循环，报告给我们：我找到了负权回路。

　　这个想法是很好的，但是如何判断碰到负权回路是个问题，读者有兴趣可以去实践一下。

　　为了处理存在负权边的情况，我们采用另外一种非常著名的方法：Bellman_Ford算法。有关最短路径的相关问题以及Dijkstra算法的求解，可参看下列博客：

　　http://www.cnblogs.com/dzkang2011/p/sp_dijkstra.html

二、Bellman_Ford算法思想

　　如果图G中存在负权回路，那么某些最短路径是不存在的。

　　Bellman_Ford算法的基本思想是：计算从源顶点s到其他所有顶点的最短路径权值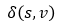，若碰上负权回路，则报告存在负权回路并返回。

　　若图中无负权回路，Bellman_Ford算法最多需要经过|V|-1次对所有边的松弛操作，就可以得到结果（有关证明请google）。当结束|V|-1次操作之后，在外围再做一次对所有边的松弛操作的测试，若到某些顶点的最短路径权值还能减小，说明|V|-1次松弛没有得到最后结果，那么必定存在负权回路，直接返回；若不再减小，说明已找到最短路。有关详情可看伪代码注释。

　　伪代码如下：

Bellman_Ford(G, w, s)

　　　　d[s]←0　　//初始化，s到s最短路权值为0，其他为正无穷

　　　　for each v∈V-{s}

　　　　　　d[v]←∞
　　　　　　
　　　　　　parent[v]← NIL　　//为生成最短路径树起作用

　　　　for i ← 1 to |V|-1　　// 实验证明最多只需|V|-1次外层循环，|V|-1次结束后，若图G中无负权回路，那么s到其他所有顶点的最短路径求得

　　　　　　do for each edge (u, v)∈E   　　//算法核心，松弛每一条边，维持三角不等式成立

　　　　　　　　do if d[v] > d[u] + w(u, v)

　　　　　　　　　　then d[v] ← d[u]+w(u, v)
　　　　　　　　　　　　
　　　　　　　　　　　　  parent[v]←u

　　　　for each edge (u, v)∈E　　　　//进行完|V|-1次循环操作后，如果还能某条边还能进行松弛，说明到某个点的最短路径还未找到，那么必定是存在负权回路，返回FALSE

　　　　　　do if d[v] > d[u] + w(u, v)

　　　　　　　　then return FALSE

　　　　return TRUE　　　　//若进行上面的松弛之后没有返回，说明所有的d值都不会再改变了，那么最短路径权值完全找到，返回TRUE

三、简单例子说明

　　下面给出一个简单的例子来模拟Bellman_Ford算法的过程，因为在|V|-1次循环中，我们需要做的是试图松弛每一条边，为了方便起见，我们给每一条边进行编号，然后按编号进行松弛，这样的话计算机实现比较方便，而且对结果不会产生影响。

　　初始情况：

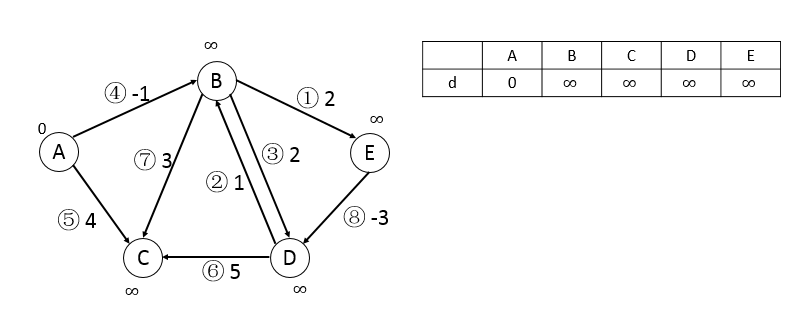
　　第一轮，按顺序可松弛边4和边5，更新顶点B和C：

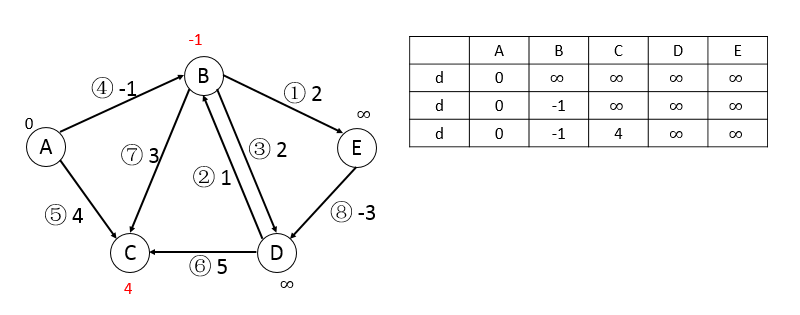
　　第二轮，按顺序可松弛边1、3、7、8，更新顶点E、D、C、D：

　　第三轮，进行一轮后发现无变化，跳出循环。

　　注：若存在负权回路，那么|V|-1必定全部做完，因为每次都可以更新，减去这个负权回路的值。

四、代码实现

　　下面给出Bellman_Ford算法的C/C++实现，其中可进行部分的优化。

　　我们发现，在进行|V|-1次循环操作时，每次的更新都与顶点的d的值有关，若所有d值不再改变了，那就不会影响到下一次的结果，那么我们就可以提前跳出循环，避免下面不必要的操作。

　　实现：

#include <iostream>
#include <cstdio>
using namespace std;

#define INF 0xffff      //权值上限
#define maxe 5000       //边数上限
#define maxn 100        //顶点数上限
int n, m;       //顶点数、边数
int d[maxn];    //保存最短路径权值的数组
int parent[maxn];  //每个顶点的前驱顶点，用以还原最短路径树
struct edge     //表述边的结构体，因为要对每一条边松弛
{
    int u, v, w;    //u为边起点，v为边端点，w为边权值，可以为负
}EG[maxe];

bool Bellman_Ford(int s)    //计算从起点到所有顶点的
{
    for(int i = 1; i <= n; i++)     //初始化操作d[EG[j].v] > d[EG[j].u]+EG[j].w
    {
        d[i] = INF;
        parent[i] = -1;
    }
    d[s] = 0;
    bool flag;      //标记，判断d值是否更新，跳出外层循环的依据
    for(int i = 1; i < n; i++)  //外层循环最多做n-1次
    {
        flag = false;   //初始为false,假设不需再更新
        for(int j = 0; j < m; j++)  //对m条边进行松弛操作，若有更新，flag记为true
            if(d[EG[j].v] > d[EG[j].u]+EG[j].w)     //if d[v] > d[u] + w(u, v)，更新d[v]
            {
                d[EG[j].v] = d[EG[j].u]+EG[j].w;
                parent[EG[j].v] = EG[j].u;
                flag = true;
            }
        if(!flag) break; //若松弛完每条边后，flag状态不变，说明未发现更新，可直接跳出循环
    }
    for(int i = 0; i < m; i++)  //做完上述松弛后，如果还能松弛，说明存在负权回路，返回false
        if(d[EG[i].v] > d[EG[i].u]+EG[i].w)
            return false;
    return true;    //不存在负权回路，返回true
}

int main()
{
    int st;
    printf("请输入n和m:
");
    scanf("%d%d", &n, &m);
    printf("请输入m条边(u, v, w)：
");
    for(int i = 0; i < m; i++)
        scanf("%d%d%d", &EG[i].u, &EG[i].v, &EG[i].w);
    printf("请输入起点：");
    scanf("%d", &st);
    if(Bellman_Ford(st))
    {
        printf("不存在负权回路。
");
        printf("源顶点到各顶点的最短路径权值为：
");
        for(int i = 1; i <= n; i++)
            printf("%d ", d[i]);
        printf("
");
    }
}

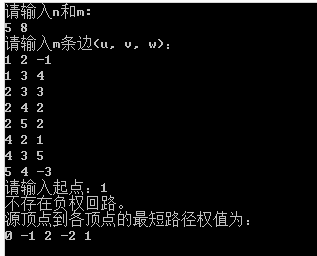
五、测试结果

就上面例子，我们进行测试，其中点都换成了数字形式：

六、时间复杂度分析

　　Bellman_Ford算法实现起来相比使用优先队列的Dijkstra算法要简单许多，但是时间复杂度不如Dijkstra算法，从代码分析，我们可以看出它的复杂度为O(VE)，V表示顶点个数，E表示边的条数。但是，至少现在我们可以对负权值情况进行求解。

（转载请注明出处。）