排序算法——堆排序

1、算法介绍

 1.1、数据结构——堆

堆是一种近似完全二叉树的数据结构，其主要性质是：节点值大于等于（小于等于）其子节点的值。

大顶堆：节点值大于等于其子节点的值，用于升序排序。

小顶堆：节点值小于等于其子节点的值，用于降序排序。

1.2、堆的构建

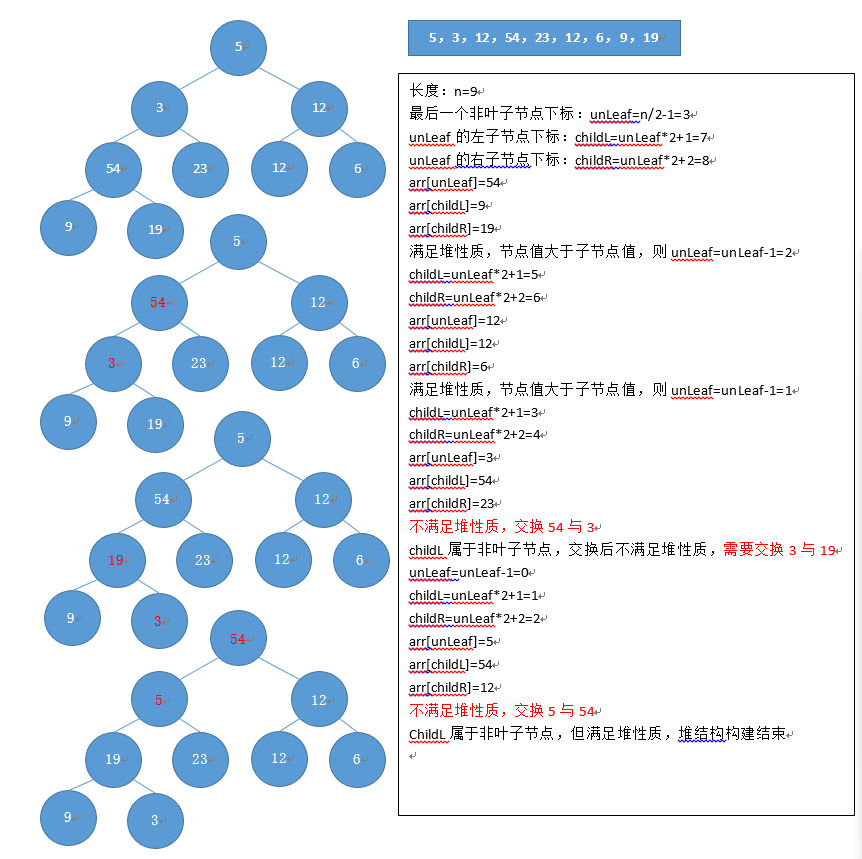
1.3、算法步骤

（1）未排序序列构建堆

（2）堆首和堆尾互换

（3）剩余未排序序列重复步骤（1）（2），直至排序完成

2、代码实现（大顶堆）

2.1、golang

package main

import (
	"fmt"
)

func main() {
	slice := []int{5, 3, 12, 54, 23, 12, 6, 9, 19}
	SortHeap(slice)
	fmt.Println(slice)
}

//堆排序
func SortHeap(slice []int) {
	n := len(slice)
	//1、建立大顶堆，从最后一个非叶子节点开始处理
	for unLeaf := n/2 - 1; unLeaf >= 0; unLeaf-- {
		heapBuildUnLeaf(slice, unLeaf)
	}
	//2、循环将堆顶的最大值至于末尾的有序区域
	for i := n - 1; i > 0; i-- {
		//fmt.Println(slice, i)
		swap(slice, 0, i)
		//由于go切片的便利性，此处不需要长度参数，直接用取0-i的切片
		heapBuildUnLeaf(slice[:i], 0)
	}
}

//处理非叶子节点
//比较 非叶子节点及其左右节点，最大值交换到非叶子节点处
func heapBuildUnLeaf(slice []int, unLeaf int) {
	n := len(slice)
	childL := unLeaf*2 + 1
	childR := unLeaf*2 + 2
	max := unLeaf //假设最大值下标
	//比较右节点
	if childR < n && slice[max] < slice[childR] {
		max = childR
	}
	//比较左节点
	if childL < n && slice[max] < slice[childL] {
		max = childL
	}
	if max != unLeaf {
		swap(slice, max, unLeaf)
		heapBuildUnLeaf(slice, max) //由于节点调整，需要递归构建
	}
}

//交换
func swap(slice []int, i, j int) {
	slice[i], slice[j] = slice[j], slice[i]
}

2.2、python3

# 堆排序
def sort_heap(arr):
    # 1、构建堆
    n = len(arr)
    for i in range(n//2-1, -1, -1):
        __heap_un_leaf(arr, i, n)
    # 2、循环将堆顶排到有序区
    for i in range(n-1, 0, -1):
        swap(arr, 0, i)
        __heap_un_leaf(arr, 0, i)


# 参数：数组，非叶子节点，处理到数组的最大长度
def __heap_un_leaf(arr, un_leaf, length):
    child_l = un_leaf*2+1
    child_r = un_leaf*2+2
    max_index = un_leaf
    if child_r < length and arr[max_index] < arr[child_r]:
        max_index = child_r
    if child_l < length and arr[max_index] < arr[child_l]:
        max_index = child_l
    if max_index != un_leaf:
        swap(arr, max_index, un_leaf)
        __heap_un_leaf(arr, max_index, length)


# 交换
def swap(arr, i, j):
    arr[i], arr[j] = arr[j], arr[i]


if __name__ == '__main__':
    arr = [5, 3, 12, 54, 23, 12, 6, 9, 19]
    sort_heap(arr)
    print(arr)