第一部分 性质与例题
转自：https://blog.csdn.net/wookaikaiko/article/details/81105031
一、关于卡特兰数
卡特兰数是一种经典的组合数，经常出现在各种计算中，其前几项为 : 1, 2, 5, 14, 42, 132, 429, 1430, 4862, 16796, 58786, 208012, 742900, 2674440, 9694845, 35357670, 129644790, 477638700, 1767263190, 6564120420, 24466267020, 91482563640, 343059613650, 1289904147324, 4861946401452, ...
二、卡特兰数的一般公式
卡特兰数满足以下性质：
令h(0)=1,h(1)=1，catalan数满足递推式。h(n)= h(0)*h(n-1)+h(1)*h(n-2) + ... + h(n-1)h(0) (n>=2)。也就是说，如果能把公式化成上面这种形式的数，就是卡特兰数。
当然，上面这样的递推公式太繁琐了，于是数学家们又求出了可以快速计算的通项公式。h(n)=c(2n,n)-c(2n,n+1)(n=0,1,2,...)。这个公式还可以更简单得化为h(n)=C(2n,n)/(n+1)。后一个公式都可以通过前一个公式经过几步简单的演算得来，大家可以拿起笔试试，一两分钟就可以搞定。
三、卡特兰数的应用
卡特兰数经常出现在OI以及ACM中，在生活中也有广泛的应用。下面举几个例子。
1、进出栈问题：栈是一种先进后出（FILO，First In Last Out）的数据结构．如下图1，1,2,3,4顺序进栈，那么一种可能的进出栈顺序是：1In→2In→2Out→3In→4In→4Out→3Out→1Out, 于是出栈序列为1,3,4,2。
那么一个足够大的栈的进栈序列为1,2,3,⋯,n时有多少个不同的出栈序列？
我们可以这样想，假设k是最后一个出栈的数。比k早进栈且早出栈的有k-1个数，一共有h(k-1)种方案。比k晚进栈且早出栈的有n-k个数，一共有h(n-k)种方案。所以一共有h(k-1)*h(n-k)种方案。显而易见，k取不同值时，产生的出栈序列是相互独立的，所以结果可以累加。k的取值范围为1至n，所以结果就为h(n)= h(0)*h(n-1)+h(1)*h(n-2) + ... + h(n-1)h(0)。
出栈入栈问题有许多的变种，比如n个人拿5元、n个人拿10元买物品，物品5元，老板没零钱。问有几种排队方式。熟悉栈的同学很容易就能把这个问题转换为栈。值得注意的是，由于每个拿5元的人排队的次序不是固定的，所以最后求得的答案要*n!。拿10元的人同理，所以还要*n!。所以这种变种的最后答案为h(n)*n!*n!。
2、二叉树构成问题。有n个结点，问总共能构成几种不同的二叉树。
我们可以假设，如果采用中序遍历的话，根结点第k个被访问到，则根结点的左子树有k-1个点、根结点的右指数有n-k个点。k的取值范围为1到n。讲到这里就很明显看得出是卡特兰数了。这道题出现在2015年腾讯实习生的在线笔试题中。
3、凸多边形的三角形划分。一个凸的n边形，用直线连接他的两个顶点使之分成多个三角形，每条直线不能相交，问一共有多少种划分方案。
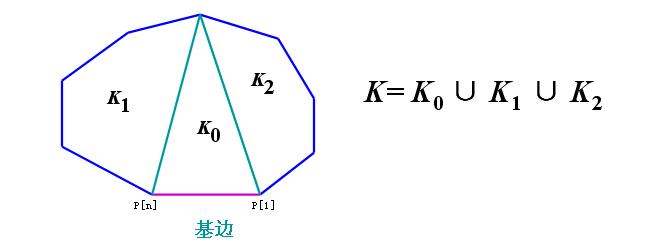
这也是非常经典的一道题。我们可以这样来看，选择一个基边，显然这是多边形划分完之后某个三角形的一条边。图中我们假设基边是p1pn，我们就可以用p1、pn和另外一个点假设为pi做一个三角形，并将多边形分成三部分，除了中间的三角形之外，一边是i边形，另一边是n-i+1边形。i的取值范围是2到n-1。所以本题的解c(n)=c(2)*c(n-1)+c(3)*c(n-2)+...c(n-1)*c(2)。令t(i)=c(i+2)。则t(i)=t(0)*t(i-1)+t(1)*t(i-2)...+t(i-1)*t(0)。很明显，这就是一个卡特兰数了。
4、有n+1个叶子的满二叉树的个数？事实上，向左记为+1，向右记为−1，按照向左优先的原则，从根节点开始遍历．例如第一个图记为+1,+1,+1,−1,−1,−1,于是由卡特兰数的含义可得满二叉树的个数为Cn。
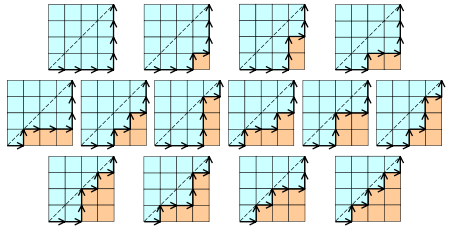
5、在n*n的格子中，只在下三角行走，每次横或竖走一格，有多少中走法？其实向右走相当于进栈，向左走相当于出栈，本质就是n个数出栈次序的问题，所以答案就是卡特兰数。（利用这个模型，我们解决这个卡特兰问题的变形问题，并顺便给进出栈问题的解法一个几何解释．）
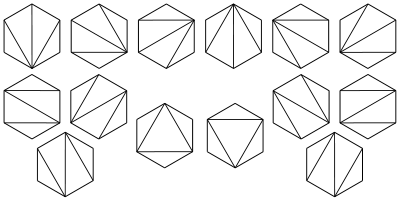
6、将一个凸n+2边形区域分成三角形区域的方法数？（答案卡特兰数）
解 先介绍两个关于卡特兰数Cn的小引理，将问题一中的+1和−1分别看成左括号和右括号，我们得到
引理一 由nn对括号形成的合法括号表达式的个数为C．
比如n=3时，所有合法的括号表达式有 :((())),(())(),()(()),()()(),(()()),共5个．
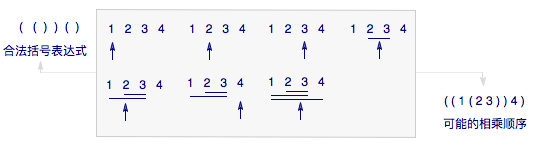
考虑n+1个数相乘，不同的相乘顺序的数目．我们可以给出每一个合法的括号表达式和一种可能的相乘顺序的对应方式．如n=3时，先取44个数a,b,c,d，然后在第一个数下设一个指针，将一个左括号看成是指针右移一格，而将右括号看成是将指针当前指向的数与其左侧的一个数作乘积，并删除左侧的那个数，那么当执行完括号表达式，就得到了一种可能的相乘顺序，如图．
这样我们就从引理一出发得到了
引理二 n+1个数连乘，不同的乘法顺序数为Cn．
注 这样也是RPN模式的计算机的工作模式，可以无需括号完成计算，从而节省按键的次数．这种计算器在财务计算中大量使用，如图．
接下来解决卡特兰问题，用1,2,3,⋯,n+2标记凸n+2边形的边，从标记为1的边的起点（按逆时针方向）开始按未标记的对角线均为向外标记方向，如图．
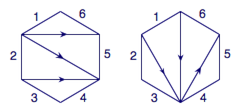(分别标记边和对角线)
进而，逆时针读图，将出的箭头读为左括号，进的箭头读为右括号，就得到了剖分方式与连乘顺序的对应．上图中的两个图对应的连乘顺序表达式分别为 ：1((2(34))5)6,(1(23))(45)6,
抛开6不计，每个连乘顺序表达式实际上就是规定了n+1个数连乘时，不同的乘法顺序，根据引理一，得到剖分方式的总数为Cn。
7、在圆上选择2n个点,将这些点成对连接起来使得所得到的n条线段不相交的方法数？和凸包切割一个原理。（答案卡特兰数）
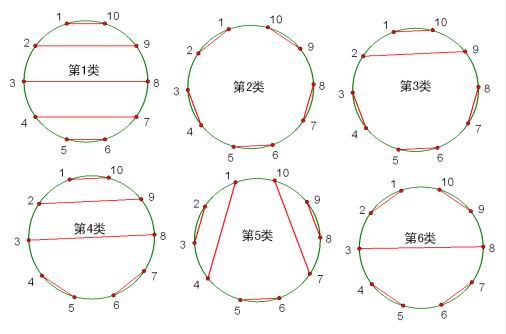
为了解决这个问题，我们重新解释卡特兰数的推导方式．先解决下面的辅助问题：(+1表示向左，-1表示向右)
圆周上有2n+1个点，其中n+1个点上标“+1”，n个点上标“−1”，如果可以找到某个标有“+1”的点作为起点，当顺时针沿圆周前进时将所遇到的点（包括起点）上标的数相加得到的和始终为正数，就称这种标记法是好标记法．求好标记法的总数（注意考虑圆排列）．
辅助问题的解 对于任何一种标记法，我们将顺时针相邻的“+1”“−1”（指顺时针前进时先遇到“+1”后遇到“−1”）同时抹去，可以证明抹去的前后对标记法的好坏没有影响．不停的重复这一过程，则最后只剩一个标有“+1”的点，显然此时标记法为好的．因此所有的标记法都是好标记法，显然其数目为 (1/2*n+1)C(2*n+1,n)-(1/n+1)C(2n,n)
问题的解 通过对辅助问题的进一步探索可知，每一种将圆周上2n+1个点标记为n+1个+1点，和n个−1点的方法唯一确定一个顺时针前进的方案（即起点）．我们将这个起点删去，剩下的2n个点在顺时针方向上一定为“+1”“−1”“+1”“−1”，…，此时将顺时针相邻的这些“+1”“−1”点用弦连接起来，就得到互不相交的n条弦．这样我们就建立了从好标记法到弦的连法的单射．
反过来，如果我们有了一种弦的连法，就可以从某条弦的端点出发顺时针前进，对每条弦的两个端点都是先遇到的端点标上“+1”，后遇到的端点标上“−1”，然后在最后回到出发点时添上一个标有“+1”的点．这样我们就建立了从弦的连法到好标记法的单射．
综上，所求的不同连法数为(1/n+1)C(2n,n)．
7、n个长方形填充一个高度为n的阶梯状图形的方法个数？把包含左上角的矩形去掉，就很容易由递推公式二推得所有填充方法数就是卡特兰数。
第二部分 源码实现
转自：https://blog.csdn.net/zuzhiang/article/details/77966726
下面给出几个求卡特兰数的公式，用h(n)表示卡特兰数的第n项，其中h(0)=1，h(1)=1
公式一：h(n)= h(0)*h(n-1)+h(1)*h(n-2) + ... + h(n-1)h(0) (n>=2)
公式二：h(n)=h(n-1)*(4*n-2)/(n+1)
公式三：h(n)=C(2n,n)/(n+1) (n=0,1,2,...)
公式四：h(n)=c(2n,n)-c(2n,n-1)(n=0,1,2,...)
下面代码用到的是公式一、公式二和公式四。
根据公式一求n<=35以内的卡特兰数，由于卡特兰数很大，超过35就超了long long 型了，所以n<=35时可以用公式一求解：
void init() { int i,j; LL h[36]; h[0]=h[1]=1; for(i=2;i<36;i++) { h[i]=0; for(j=0;j<i;j++) h[i]=h[i]+h[j]*h[i-j-1]; } }
如果n>35时求h(n)%p应该怎么求呢？由于h(n)是大数，这里可以借助Lucas（卢卡斯）定理来解决。
Lucas定理：Lucas定理是用来求 c(n,m) mod p，p为素数的值。Lucas定理的表达式为：Lucas(n,m,p)=c(n%p,m%p)*Lucas(n/p,m/p,p) 有了这个公式，我们直接看Lucas定理的代码：
//Lucas定理实现C(n,m)%p的代码： LL exp_mod(LL a, LL b, LL p) { //快速幂取模 LL res = 1; while(b != 0) { if(b&1) res = (res * a) % p; a = (a*a) % p; b >>= 1; } return res; } LL Comb(LL a, LL b, LL p) { //求组合数C(a,b)%p if(a < b) return 0; if(a == b) return 1; if(b > a - b) b = a - b; LL ans = 1, ca = 1, cb = 1; for(LL i = 0; i < b; ++i) { ca = (ca * (a - i))%p; cb = (cb * (b - i))%p; } ans = (ca*exp_mod(cb, p - 2, p)) % p; return ans; } LL Lucas(LL n,LL m,LL p) { //Lucas定理求C(n,m)%p LL ans = 1; while(n&&m&&ans) { ans = (ans*Comb(n%p, m%p, p)) % p; n /= p; m /= p; } return ans; }
这样根据公式四：h(n)=c(2n,n)-c(2n,n-1)(n=0,1,2,...) 就可以利用Lucas定理来求 ：
h(n)%p=(Lucas(2n,n,p)-Lucas(2n,n-1,p)+p)%p。怎么理解呢？对于两个数a，b，(a-b)%p=(a%p-b%p)%p；那括号里为什么还要再加一个p呢？因为取模前前者一定大于后者，相减一定为正，而取模后就不一定了，所以要加一个p，保证是正数。
如果是要求卡特兰大数呢？只要顺便实现大数的一些运算就好了。下面直接给出代码：
int a[101][101],b[101]; void catalan() //求卡特兰数 { int i, j, len, carry, temp; a[1][0] = b[1] = 1; len = 1; for(i = 2; i <= 100; i++) { for(j = 0; j < len; j++) //乘法 a[i][j] = a[i-1][j]*(4*(i-1)+2); carry = 0; for(j = 0; j < len; j++) //处理相乘结果 { temp = a[i][j] + carry; a[i][j] = temp % 10; carry = temp / 10; } while(carry) //进位处理 { a[i][len++] = carry % 10; carry /= 10; } carry = 0; for(j = len-1; j >= 0; j--) //除法 { temp = carry*10 + a[i][j]; a[i][j] = temp/(i+1); carry = temp%(i+1); } while(!a[i][len-1]) //高位零处理 len --; b[i] = len; } }
以上可以处理n<=100时的卡特兰大数，n再大可以把数组相应开大。其中b[i]保存的是第i位卡特兰数的长度，a[i]数组保存的是第i位卡特兰数的数值，高位存高位，低位存低位。
最后再简单说一下卡特兰数的应用，网上也给出了很多很好的解析，我只是把我觉得重要的整合了一下：
卡特兰数的应用都可以归结到一种情况：有两种操作，分别为操作一和操作二，它们的操作次数相同，都为 N，且在进行第 K 次操作二前必须先进行至少 K 次操作一，问有多少中情况？结果就Catalan(N)。
Catalan数的典型应用：
1.由n个+1和n个-1组成的排列中，满足前缀和>=0的排列有Catalan(N)种。
2.括号化问题。左括号和右括号各有n个时，合法的括号表达式的个数有Catalan(N)种。
3.有n+1个数连乘，乘法顺序有Catalan(N)种,相当于在式子上加括号。
4.n个数按照特定顺序入栈，出栈顺序随意，可以形成的排列的种类有Catalan(N)种。
5.给定N个节点，能构成Catalan(N)种种形状不同的二叉树。
6.n个非叶节点的满二叉树的形态数为Catalan(N)。
7.对于一个n*n的正方形网格，每次只能向右或者向上移动一格，那么从左下角到右上角的不同种类有Catalan(N)种。
8.对于在n位的2进制中，有m个0，其余为1的catalan数为：C（n,m）-C(n,m-1)。
9.对凸n+2边形进行不同的三角形分割（只连接顶点对形成n个三角形）数为Catalan(N)。
10.将有2n个元素的集合中的元素两两分为n个子集，若任意两个子集都不交叉，那么我们称此划分为一个不交叉划分。此时不交叉的划分数是Catalan(N)。
11.n层的阶梯切割为n个矩形的切法数也是Catalan(N)。
12.在一个2*n的格子中填入1到2n这些数值使得每个格子内的数值都比其右边和上边的所有数值都小的情况数也是Catalan(N)。