https://ac.nowcoder.com/acm/contest/894/E
一开始写了一个简单的模拟 通过率只有5%......
看题解真的理解了好久!!肥宅大哭orz
题解如下

最后一句:“维护6个树状数组即可”.....喵喵喵??
先学一下树状数组吧:
链接在这
https://blog.csdn.net/Small_Orange_glory/article/details/81290634
结合代码讲比较容易理解
#include<bits/stdc++.h> using namespace std; const int maxn=4e6+100; const int T=3e5+10; const int mod=1e9+7; const int g=10; #define ll long long ll bit[8][maxn]; void add(ll b[],int i,ll C) //更新树状数组 { while(i<maxn) { b[i]=(b[i]+C)%mod; i+=i&-i; } } ll sum(ll b[],int i) //求和 前i个元素的和 { ll ans=0; while(i>0) { ans+=b[i]; i-=i&-i; } return ans%mod; } int main() { int Q;scanf("%d",&Q); while(Q--) { int op,v,t,m;scanf("%d%d%d",&op,&v,&t); if(op==1) { int V=v+g*(T-t); scanf("%d",&m); add(bit[1],V,1LL*m*v%mod*v%mod); add(bit[2],V,1LL*m*g*g%mod); add(bit[3],V,1LL*m*g*g%mod*t%mod*t%mod); add(bit[4],V,1LL*2*m*g*g%mod*t%mod); add(bit[5],V,1LL*2*m*v%mod*g%mod); add(bit[6],V,1LL*2*m*v%mod*g*t%mod); } else { int V=min(v+g*(T-t),maxn-1); ll ans=0; ans+=sum(bit[1],V); ans+=sum(bit[2],V)*t%mod*t%mod; ans+=sum(bit[3],V); ans-=sum(bit[4],V)*t%mod; ans+=sum(bit[5],V)*t%mod; ans-=sum(bit[6],V); ans%=mod; if(ans<0) ans+=mod; printf("%lld\n",ans); } } return 0; }
先讲为什么维护6个数组:
因为将公式
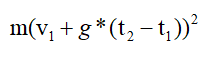
拆开就会变成含有6项的多项式:
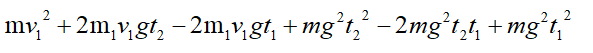
我们将符合条件的小球的分别记录到6个数组中 这样方便求和
那么什么是符合条件的小球呢?
仔细看题解里说:
若某一时刻a球比b球速度快,则a球始终比b球速度快。
所以如果末尾时间a球比b球快 那么a球始终比b球快
所以判断某一时刻速度比v小的小球有哪些 假设在这一时刻扔下一个初速度为v的小球 只需要看哪些小球在最后的时刻速度比这个初速度为v的小球速度慢就好了
那么对于每一次op==1 我们就更新一次数组 把v+g*(T-t)之后的树状数组全部更新
对于每一次op==2 我们就把前v+g*(T-t)项求和
照着模拟几遍就理解了(而我想了一晚上)