一:堆结构
堆是具有以下性质的完全二叉树:每个结点的值都大于或等于其左右孩子结点的值,称为大顶堆;或者每个结点的值都小于或等于其左右孩子结点的值,称为小顶堆。
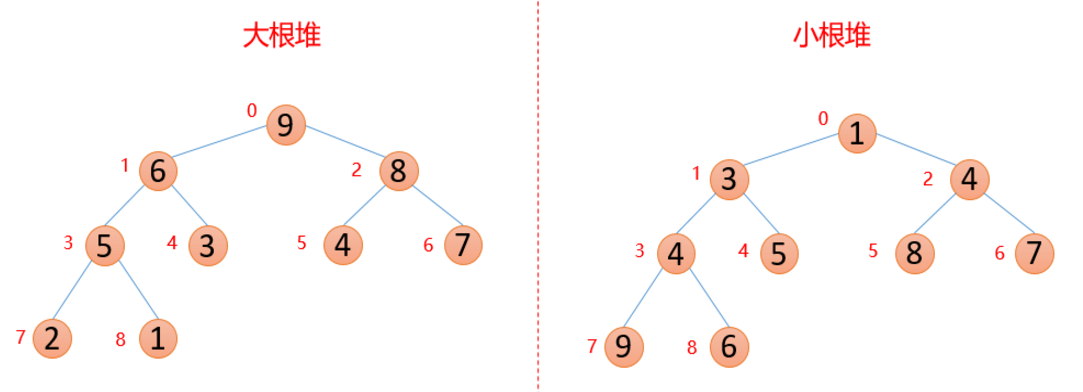
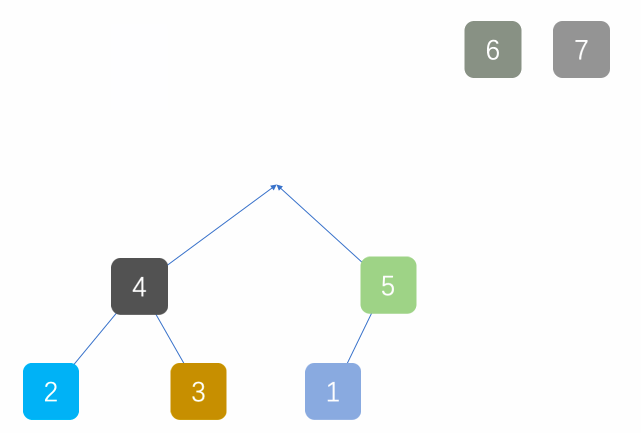
上图中每个数都进行了标记,上面的结构映射成数组就变成
查找数组中某个数的父结点和左右孩子结点,比如已知索引为i的数,那么
1.父结点索引:(i-1)/2(这里计算机中的除以2,省略掉小数)
2.左孩子索引:2*i+1
3.右孩子索引:2*i+2
所以上面两个数组可以脑补成堆结构,因为他们满足堆的定义性质:大根堆:arr(i)>arr(2*i+1) && arr(i)>arr(2*i+2),小根堆:arr(i)<arr(2*i+1) && arr(i)<arr(2*i+2)
二:堆排序
算法步骤
- 创建一个大根堆 H[0……n-1],数组的最大值在大根堆的顶端;
- 将顶端的数与末尾的数交换,末尾的数为最大值,将剩余的n-1个数再构造成大根堆。
- 重复步骤 2,直到堆的尺寸为 1。
待排序数组
第一步:创建大根堆,根据上面的原则,下面有动图。
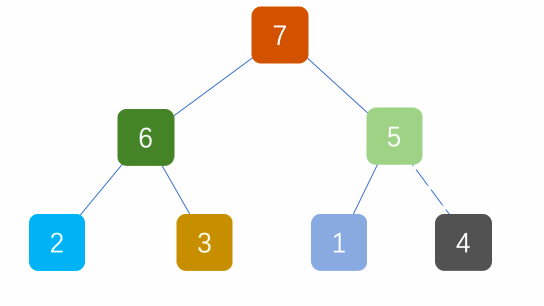
第二步:将顶端的数与末尾的数交换,末尾的数为最大值,将剩余的6个数再构造成大根堆。
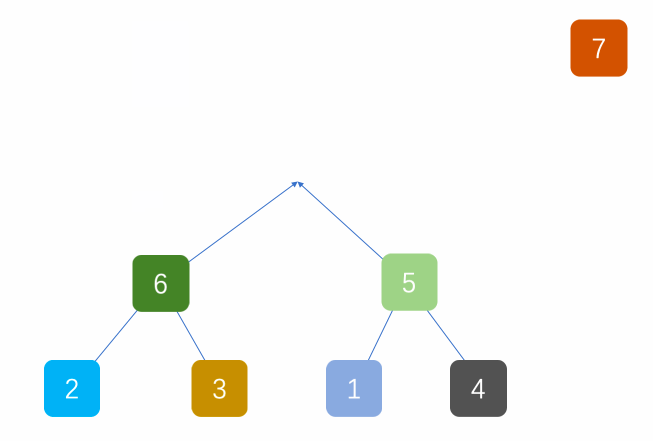 ——->
——->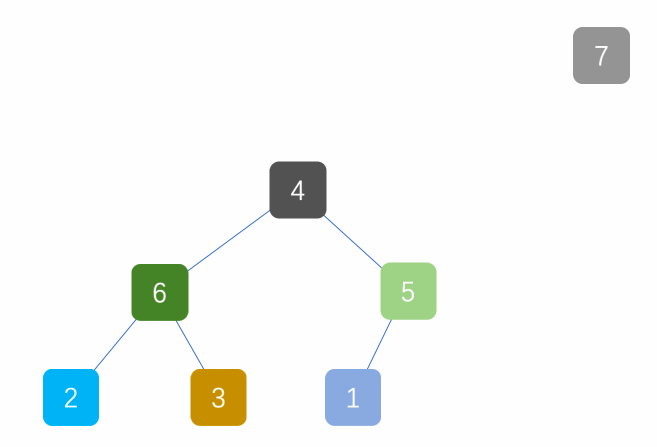 ——->
——->
图一和图二是将顶端和末端交换,图三是从新创建大根堆的过程。
第三步:将顶端的数与末尾的数交换,末尾的数为最大值,将剩余的n-1个数再构造成大根堆。
 ——->........省略
——->........省略
最后得到排序后的数组 : 
三:排序动图

四:堆排序的时间复杂度和空间复杂度
在取出堆顶点放到对应位置并把原堆的最后一个节点填充到堆顶点之后,需要对堆进行重建,重建堆一共需要n-1次循环,每次循环的比较次数为log(i),所以时间复杂度为O(nlogn)。
空间复杂度为O(1)
五:堆排序代码实现
/** * 堆排序 */ public class HeapSort { public static void main(String[] args) { int[] nums = {5,2,7,3,6,1,4}; headSort(nums); } public static void headSort(int[] list) { //构造初始堆,从第一个非叶子节点开始调整,左右孩子节点中较大的交换到父节点中 for (int i = (list.length) / 2 - 1; i >= 0; i--) { headAdjust(list, list.length, i); } //排序,将最大的节点放在堆尾,然后从根节点重新调整 for (int i = list.length - 1; i >= 1; i--) { int temp = list[0]; list[0] = list[i]; list[i] = temp; headAdjust(list, i, 0); } } private static void headAdjust(int[] list, int len, int i) { int k = i, temp = list[i], index = 2 * k + 1; while (index < len) { if (index + 1 < len) { if (list[index] < list[index + 1]) { index = index + 1; } } if (list[index] > temp) { list[k] = list[index]; k = index; index = 2 * k + 1; } else { break; } } list[k] = temp; } }