第七讲、最优化
1.优化目标
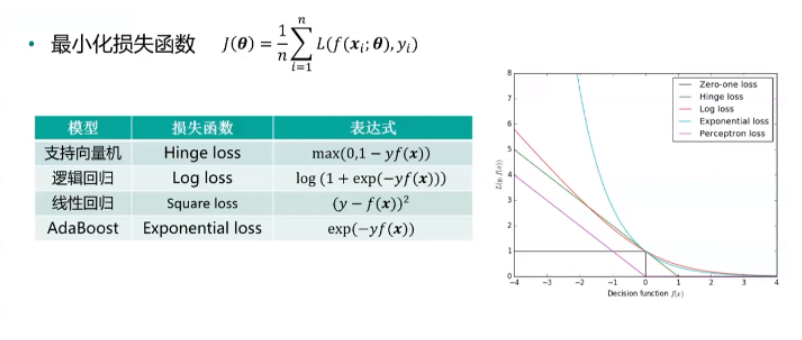
2.梯度下降
①batch

②随机梯度下降SGD
训练一个样本,更新—次参数; mini-batch是SGD的推广,通常所说SGD即是mini-batch。

③病态条件
病态条件:不同方向有不同的梯度;学习率的选择困难。
④局部最小
局部最小(local minima) 权重空间是对称的/放大或者缩小权重。
以前的观点:局部最小是一个严重的问题。
现在:情况不同!
部最小非常接近于训练误差;实验和理论支持
⑤鞍点
鞍点(saddle points) 梯度为0,Hessian矩阵同时存在正值和负值
Heissan矩阵的所有特征值为正值的概率很低·
对于高维情况,鞍点和局部最小点的数量多
⑥平台
定义:梯度为零,hessian矩阵也为0
加入噪音使得从平台区域跳出。
⑦梯度爆炸与悬崖 在RNN中非常常见,参数不断相乘导致;
长期时间依赖性。
解决办法:梯度截断(gradient clipping),启发式梯度截断干涉以减少步长。
3.动量法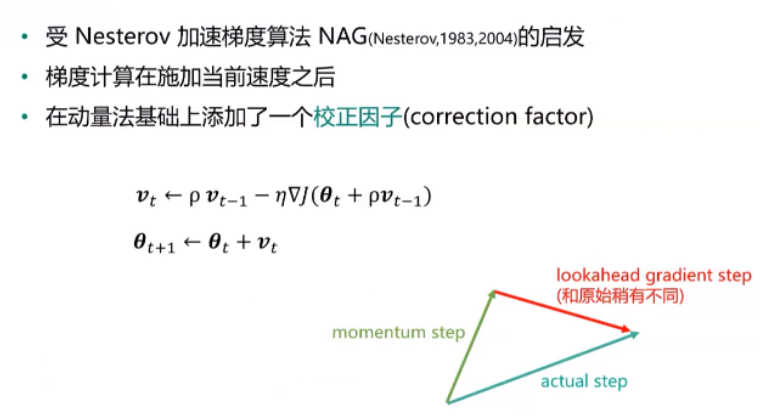

·p也可以随着迭代次数的增大而变大随着时间推移调整p比收缩n更重要。
动量法克服了SGD中的两个问题:
-
Hessian矩阵的病态问题(右图解释)·
-
随机梯度的方差带来的不稳定。
②Nesterov动量法


③AdaGrad

④RMSPro
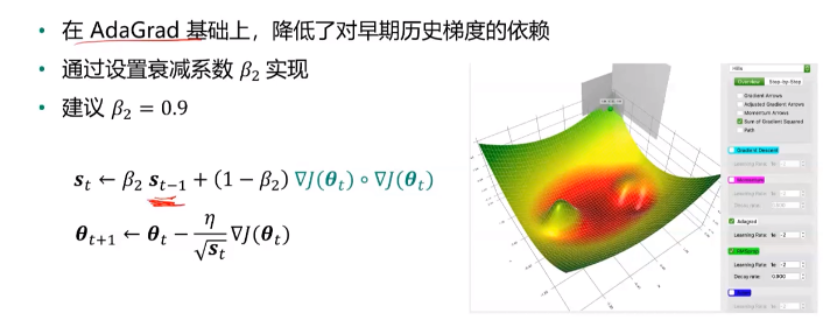
⑥adam
