1506.01186-Cyclical Learning Rates for Training Neural Networks
论文中提出了一种循环调整学习率来训练模型的方式。
如下图:
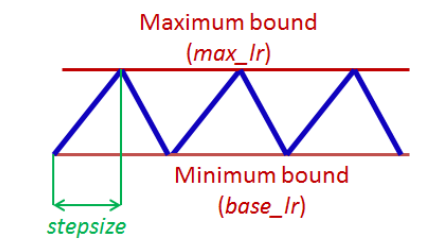
通过循环的线性调整学习率,论文作者观察到的一种比较典型的曲线如下图:
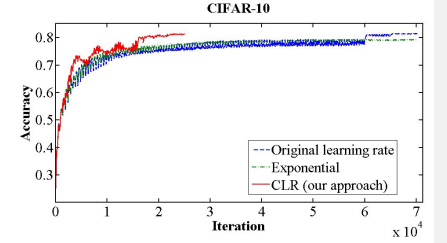
图中,使用循环调整方式的模型,虽然训练中准确度有很大的波动,但是这种波动并不影像模型很快的收敛,并且以更快的速度收敛到了固定学习率或者学习率衰减方案中能达到的最高准确率。
这种方式需要设置的超参有三个, min bound,max bound ,step size。
step size一般选择epoch的step数的2-8倍。例如一个epoch里面有500步,则2000作为step size是不错的选择。
确定step size之后,使用一个简短的训练来确定 min-max bound,在一个训练里,以循环学习率的方式,线性的提升学习率,画出学习率与准确率关系的曲线。模型准确率最快增长的学习率适合用来做min bound,模型准确率增长减缓甚至直接出现负增长的地方,适合作max bound。如下图中所示:
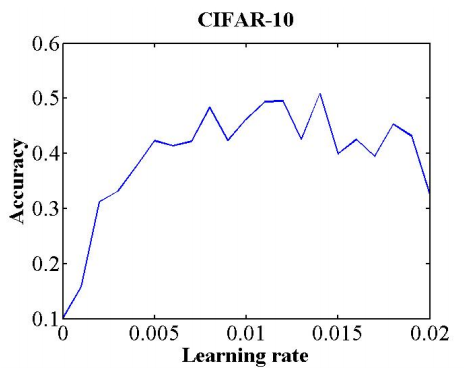
模型一开始就出现了很快的准确率增长,所以选择0.001作为min bound,而0.005的位置出现了负增长,这里作为max bond。
另外论文提出了另外两种变种:
-
triangular2; the same as the triangular policy except the learning rate difference is cut in half at the end of each cycle. This means the learning rate difference drops after each cycle.
每次cycle之间才做一次lr decay
-
exp range; the learning rate varies between the minimum and maximum boundaries and each boundary value declines by an exponential factor of gamme^iteration
随着每个iteration都做一次lr decay
论文还尝试把循环学习率与各种优化算法都结合了一下,但是看结果,除了nestrov动量法,其他几种优化算法的效果都不好。
这是可以理解的,因为除了单纯的动量法,其他几种方法,都会针对学习率进行动态的调整。而循环学习率引入的学习率循环变化必然会破坏学习率动态调整的某些特性。所以结果就变得无法估计。
另外,针对学习率固定decay的效果与循环学习率的对比,论文作者单独设计了一个实验,循环学习率只循环一次,在学习率达到最小的时候,就固定住,或者做decay,不再上升,但是最后的结果,还是不如循环学习率的效果好。
这种循环学习率的方式,似乎是因为循环引入了更多的随机性?让梯度有了更多的机会往不同的方向探索?
论文中没有提出很好的理论解释。