T11 music
LYK loves music (music)
Time Limit:4000ms Memory Limit:详见数据范围
题目描述
LYK喜欢听音乐,它的歌单里共有 n首音乐,而且它每次听音乐时都是连续地听 m首,
它甚至能记得自己给每首音乐的评分ai。
现在它想选择一首歌开始听,使得接下来连续 m首歌的评分<xi 的歌最少。
当然它最开始听的歌也是需要在一段区间[li,ri]内选择的。
现在它想让你帮它挑选一首最开始听的歌,使得以这首歌开始的m首歌中,评分<xi 的
歌最少。
输入格式(music.in)
第一行输入2个数 n,m。
接下来一行n个数 ai表示第i首歌的评分。
接下来一行一个 Q,表示有Q次询问。
接下来Q行,每行 3个数li,ri,qi。为了体现询问的在线性,对于该询问, xi=ans{i-1}^qi。
其中^表示异或,ans{i-1}表示上一问的答案,若 i=1,则ans{i-1}=0。
输出格式(music.out)
Q 行,表示评分<xi的歌最少是多少。
样例输入
5 3
1 2 1 2 3
5
1 1 2
1 3 2
1 3 3
1 3 5
1 3 1
样例输出
2
0
2
3
1
数据范围
对于测试点1,2:n,Q<=100。
对于测试点3,4:n,Q<=1000。
对于测试点5,6:m=1。
对于测试点7,8,9,10:n,Q<=200000。
对于测试点1~8:内存限制为 256MB,1<=li<=ri<=n-m+1,0<=ai,qi<2^30,1<=m<=n。
对于测试点9~10:内存限制为 70MB,1<=li<=ri<=n-m+1,0<=ai,qi<2^30,1<=m<=n。
思路:我们发现,m对于所有询问都是一样,所以可以从这里下手。 考虑对于每个小于 xi 的数,他能影响的区间(起点) [max(i - m + 1, 1), i],那么考虑把这个区间都 + 1,考虑不在线的话,对于 xi 排序,从小到大,然后就是一个区间最小值。对于在线的话,主席树就好了。 区间加,区间最小值(当然是前缀) 的新姿势
#include<iostream>
#include<cstdio>
#include<algorithm>
#define maxn 200010
#define INF 10000000
using namespace std;
int n, m, la, q;
int read(){
int x = 0; char c = getchar();
while(c < '0' || c > '9') c = getchar();
while(c >= '0' && c <= '9'){x = x * 10 + c - '0'; c = getchar();}
return x;
}
struct node{
int v, id;
friend bool operator < (node x, node y){return x.v < y.v;}
}a[maxn];
int my_lower_bound(int l, int r, int v){
int mid, ans = 0;
while(l <= r){
mid = l + r >> 1;
if(a[mid].v < v) ans = mid, l = mid + 1;
else r = mid - 1;
}
return ans;
}
#define lc T[i].ch[0]
#define rc T[i].ch[1]
#define Lc T[j].ch[0]
#define Rc T[j].ch[1]
struct zhuxi{
int v, ch[2], lz;
}T[maxn * 80]; int rt[maxn], top;
inline void maintain(int i){
T[i].v = T[i].lz + min(T[lc].v, T[rc].v);
}
void update(int &i, int j, int l, int r, int L, int R, int v){
if(l > R || r < L) return ; i = ++top;
T[i] = T[j]; int m = l + r >> 1;
if(L <= l && r <= R) T[i].lz += v;
else {update(lc, Lc, l, m, L, R, v); update(rc, Rc, m + 1, r, L, R, v);}
maintain(i);
}
int query(int i, int l, int r, int L, int R){
if(l > R || r < L) return INF;
if(L <= l && r <= R) return T[i].v;
int m = l + r >> 1;
return T[i].lz + min(query(lc, l, m, L, R), query(rc, m + 1, r, L, R));
}
int main(){
n = read(); m = read();
for(int i = 1; i <= n; ++i) a[a[i].id = i].v = read();
sort(a + 1, a + n + 1);
for(int i = 1; i <= n; ++i) update(rt[i], rt[i - 1], 1, n, max(a[i].id - m + 1, 1), a[i].id, 1);
q = read();
for(int i = 1; i <= q; ++i){
int x, y, z, k; x = read(); y = read(); z = read(); z ^= la;
k = my_lower_bound(1, n, z);
printf("%d
", (la = query(rt[k], 1, n, x, y)));
}
return 0;
}
T12 洛谷 P4137 Rmq Problem / mex
题目描述
有一个长度为n的数组{a1,a2,…,an}。m次询问,每次询问一个区间内最小没有出现过的自然数。
输入输出格式
输入格式:
第一行n,m。
第二行为n个数。
从第三行开始,每行一个询问l,r。
输出格式:
一行一个数,表示每个询问的答案。
输入输出样例
输入样例#1:
5 5
2 1 0 2 1
3 3
2 3
2 4
1 2
3 5
输出样例#1:
1
2
3
0
3
说明
对于30%的数据:1<=n,m<=1000
对于100%的数据:1<=n,m<=200000,0<=ai<=10^9,1<=l<=r<=n
思路:考虑离线,将询问按照左端点排序,考虑左端点为 1 的时候,显然可以 O(n) 处理出对于所有右端点的答案。考虑左端点 + 1 会发生什么,也就是 a[l] 这个数会消失,定义 nxt[i] 为 a[i] 这个数在序列中出现在 i 之后的下个位置,也就是说对于区间 [i + 1, nxt[i] - 1] 这个数都消失了,也就是说这个区间的答案可以为 a[i] (当然也可能更小),所以发现这是一个区间修改,并且右端点只会移动 n 次,所以复杂度为 O(nlogn)。 另外, a[i] 最高可达 1e9,其实没有意义,因为答案最大也就是 n + 1,所以大于 n 的变成 n + 1 即可。
#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cstring>
#define INF 2147483647
#define maxn 200010
#define ll long long
using namespace std;
int n, m, t, a[maxn], ans[maxn], mex[maxn];
//map<int, int> nxt, vis;
int nxt[maxn], vis[maxn];
int read(){
int x = 0; char c = getchar();
while(c < '0' || c > '9') c = getchar();
while(c >= '0' && c <= '9'){x = x * 10 + c - '0'; c = getchar();}
return x;
}
struct Query{
int l, r, id;
friend bool operator < (Query x, Query y){return x.l < y.l;}
}Q[maxn];
#define lc i << 1
#define rc i << 1 | 1
struct segment{
int v, lz;
segment(){lz = INF;}
}T[maxn << 2];
inline void pushdown(int i, int l, int r){
if(T[i].lz == INF) return ; int m = l + r >> 1;
if(m - l + 1 == 1) T[lc].v = min(T[lc].v, T[i].lz);
if(m - l + 1 != 1) T[lc].lz = min(T[lc].lz, T[i].lz);
if(r - m == 1){T[rc].v = min(T[rc].v, T[i].lz);}
if(r - m != 1) T[rc].lz = min(T[rc].lz, T[i].lz);
}
void build(int i, int l, int r){
if(l == r){T[i].v = mex[l]; return ;}
int m = l + r >> 1;
build(lc, l, m); build(rc, m + 1, r);
}
void update(int i, int l, int r, int L, int R, int v){
if(l > R || r < L) return;
if(L <= l && r <= R){
T[i].lz = min(T[i].lz, v);
if(l == r) T[i].v = min(T[i].v, v);
return ;
}
int m = l + r >> 1; pushdown(i, l, r);
update(lc, l, m, L, R, v); update(rc, m + 1, r, L, R, v);
}
int query(int i, int l, int r, int k){
if(l == r) return T[i].v;
int m = l + r >> 1; pushdown(i, l, r);
if(k <= m) return query(lc, l, m, k);
else return query(rc, m + 1, r, k);
}
int main(){
n = read(); m = read(); //t = read();
for(int i = 1; i <= n; ++i){a[i] = read(); if(a[i] > n) a[i] = n + 1;}
for(int i = 1; i <= m; ++i){
Q[i].l = read(); Q[i].r = read();
Q[i].id = i;
}
sort(Q + 1, Q + m + 1);
for(int i = n; i >= 1; --i){
if(!vis[a[i]]) nxt[i] = n + 1;
else nxt[i] = vis[a[i]];
vis[a[i]] = i;
}
int now = 0; memset(vis, 0, sizeof vis);
for(int i = 1; i <= n; ++i){
vis[a[i]] = 1;
while(vis[now]) ++now;
mex[i] = now;
}
build(1, 1, n);
int la = 1;
for(int i = 1, j = 1; i <= n && j <= m; ++i){
while(Q[j].l == i){
ans[Q[j].id] = query(1, 1, n, Q[j].r);
++j;
}
update(1, 1, n, 1, nxt[i] - 1, a[i]);
}
for(int i = 1; i <= m; ++i) printf("%d
", ans[i]);
return 0;
}
显然可以莫队,不可虑复杂度的话。不知为啥洛谷 90 分
#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cmath>
#define maxn 200010
using namespace std;
int n, m, a[maxn], ans[maxn];
int read(){
int x = 0; char c = getchar();
while(c < '0' || c > '9') c = getchar();
while(c >= '0' && c <= '9'){x = x * 10 + c - '0'; c = getchar();}
return x;
}
int block;
struct Query{
int l, r, id;
friend bool operator < (Query x, Query y){
if(x.l / block == y.l / block) return x.r < y.r;
return x.l / block < y.l / block;
}
}Q[maxn];
int num[maxn], mex;
void add(int i){
++num[a[i]];
while(num[mex]) mex++;
}
inline void del(int i){
if(--num[a[i]] == 0) mex = min(mex, a[i]);
}
int main(){
n = read(); m = read(); block = sqrt(n);
for(int i = 1; i <= n; ++i){a[i] = read(); if(a[i] > n) a[i] = n + 1;}
for(int i = 1; i <= m; ++i){Q[i].l = read(); Q[i].r = read(); Q[i].id = i;}
sort(Q + 1, Q + m + 1);
int l = Q[1].l, r = l - 1;
for(int i = 1; i <= m; ++i){
while(l < Q[i].l) del(l++);
while(l > Q[i].l) add(--l);
while(r > Q[i].r) del(r--);
while(r < Q[i].r) add(++r);
ans[Q[i].id] = mex;
}
for(int i = 1; i <= m; ++i) printf("%d
", ans[i]);
return 0;
}
其实可以做到动态,那么就是主席树了,不知道该如何解释
#include<iostream>
#include<cstdio>
#define maxn 200010
using namespace std;
int n, m, t, pre[maxn], vis[maxn], a[maxn];
int read(){
int x = 0; char c = getchar();
while(c < '0' || c > '9') c = getchar();
while(c >= '0' && c <= '9'){x = x * 10 + c - '0'; c = getchar();}
return x;
}
#define lc T[i].ch[0]
#define rc T[i].ch[1]
#define Lc T[j].ch[0]
#define Rc T[j].ch[1]
struct zhuxi{
int v, ch[2];
}T[maxn * 20]; int top, rt[maxn];
void update(int &i, int j, int l, int r, int k, int v){
i = ++top; int m = l + r >> 1;
T[i] = T[j]; if(l == r){T[i].v = v; return ;}
if(k <= m) update(lc, Lc, l, m, k, v);
else update(rc, Rc, m + 1, r, k, v);
T[i].v = min(T[lc].v, T[rc].v);
}
int query(int i, int l, int r, int k){
if(l == r) return l;
int m = l + r >> 1;
if(T[lc].v < k) return query(lc, l, m, k);
else return query(rc, m + 1, r, k);
}
int main(){
n = read(); m = read(); //t = read();
for(int i = 1; i <= n; ++i){a[i] = read(); if(a[i] > n) a[i] = n + 1;}
for(int i = 1; i <= n; ++i) update(rt[i], rt[i - 1], 0, n + 1, a[i], i); //在 a[i] 这个位置,权值是 i,即出现位置
for(int i = 1; i <= m; ++i){
int x, y; x = read(); y = read();
printf("%d
", query(rt[y], 0, n + 1, x)); //在添加了 a[1] ~ a[r] 的树上找最后出现位置小于 l 的数字
}
return 0;
}
T13 洛谷 P3302 [SDOI2013]森林
题目描述
小Z有一片森林,含有N个节点,每个节点上都有一个非负整数作为权值。初始的时候,森林中有M条边。
小Z希望执行T个操作,操作有两类:
Q x y k查询点x到点y路径上所有的权值中,第k小的权值是多少。此操作保证点x和点y连通,同时这两个节点的路径上至少有k个点。L x y在点x和点y之间连接一条边。保证完成此操作后,仍然是一片森林。
为了体现程序的在线性,我们把输入数据进行了加密。设lastans为程序上一次输出的结果,初始的时候lastans为0。
- 对于一个输入的操作
Q x y k,其真实操作为Q x^lastans y^lastans k^lastans。- 对于一个输入的操作
L x y,其真实操作为L x^lastans y^lastans。其中^运算符表示异或,等价于pascal中的xor运算符。
请写一个程序來帮助小Z完成这些操作。
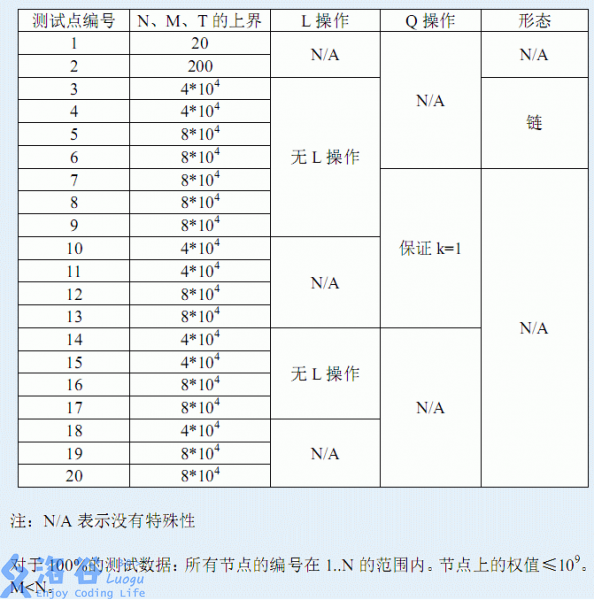
对于所有的数据,n,m,T<= 8∗1048*10^48∗104 .
输入输出格式
输入格式:
第一行包含一个正整数testcase,表示当前测试数据的测试点编号。保证1<=testcase<=20。
第二行包含三个整数N,M,T,分别表示节点数、初始边数、操作数。
第三行包含N个非负整数表示 N个节点上的权值。
接下来 M行,每行包含两个整数x和 y,表示初始的时候,点x和点y 之间有一条无向边。
接下来 T行,每行描述一个操作,格式为”Q x y k“或者”L x y “,其含义见题目描述部分。
输出格式:
对于每一个第一类操作,输出一个非负整数表示答案。
输入输出样例
输入样例#1:
1
8 4 8
1 1 2 2 3 3 4 4
4 7
1 8
2 4
2 1
Q 8 7 3 Q 3 5 1
Q 10 0 0
L 5 4
L 3 2 L 0 7
Q 9 2 5 Q 6 1 6
输出样例#1:
2
2
1
4
2
说明
对于第一个操作 Q 8 7 3,此时 lastans=0,所以真实操作为Q 8^0 7^0 3^0,也即Q 8 7 3。点8到点7的路径上一共有5个点,其权值为4 1 1 2 4。
这些权值中,第三小的为 2,输出 2,lastans变为2。
对于第二个操作 Q 3 5 1 ,此时lastans=2,所以真实操作为Q 3^2 5^2 1^2 ,也即Q 1 7 3。点1到点7的路径上一共有4个点,其权值为 1 1 2 4 。
这些权值中,第三小的为2,输出2,lastans变为 2。之后的操作类似。
思路:显然不考虑 L 操作的话,这就是个裸的主席树。那么考虑 L 操作,发现可以启发式合并,总的复杂度为 (O(nlog_2n)),然后就可以过了。时间复杂度 (O(n*{log_2}^2n)),空间复杂度 (O(n*{log_2}^2n))
#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#define maxn 80010
using namespace std;
int n, m, k;
struct Edge{
int to, next;
}e[maxn << 1]; int c1, head[maxn];
inline void add_edge(int u, int v){
e[c1].to = v; e[c1].next = head[u]; head[u] = c1++;
}
int fa[maxn], sz[maxn];
int find(int x){return fa[x] == x ? x : fa[x] = find(fa[x]);}
int b[maxn], a[maxn], cnt;
void init_hash(){
scanf("%d%d%d", &n, &m, &k);
for(int i = 1; i <= n; ++i){scanf("%d", &a[i]), b[i] = a[i];}
sort(b + 1, b + n + 1); cnt = unique(b + 1, b + n + 1) - b - 1;
for(int i = 1; i <= n; ++i) a[i] = lower_bound(b + 1, b + cnt + 1, a[i]) - b;
}
#define lc T[i].ch[0]
#define rc T[i].ch[1]
#define Lc T[j].ch[0]
#define Rc T[j].ch[1]
struct zhuxi{
int v, ch[2];
}T[maxn * 400]; int rt[maxn], top;
void update(int &i, int j, int l, int r, int k, int v){
i = ++top;
T[i] = T[j]; T[i].v += v;
if(l == r) return ; int m = l + r >> 1;
if(k <= m) update(lc, Lc, l, m, k, v);
else update(rc, Rc, m + 1, r, k, v);
}
int query(int i, int j, int lca, int flca, int l, int r, int k){
if(l == r) return b[l]; int v = T[lc].v + T[Lc].v - T[T[lca].ch[0]].v - T[T[flca].ch[0]].v;
int m = l + r >> 1;
if(k <= v) return query(lc, Lc, T[lca].ch[0], T[flca].ch[0], l, m, k);
else return query(rc, Rc, T[lca].ch[1], T[flca].ch[1], m + 1, r, k - v);
}
bool vis[maxn]; int f[maxn][21], dep[maxn];
void dfs(int u, int fa){
vis[u] = 1; dep[u] = (~fa ? dep[fa] + 1 : 1); f[u][0] = (~fa ? fa : 0);
for(int i = 1; i <= 20; ++i) f[u][i] = f[f[u][i - 1]][i - 1];
update(rt[u], rt[(~fa ? fa : 0)], 1, cnt, a[u], 1);
for(int i = head[u]; ~i; i = e[i].next){
int v = e[i].to; if(v == fa) continue;
dfs(v, u);
}
}
int get_lca(int x, int y){
if(dep[x] < dep[y]) swap(x, y);
for(int i = 20; i >= 0; --i)
if(dep[f[x][i]] >= dep[y]) x = f[x][i];
if(x == y) return x;
for(int i = 20; i >= 0; --i)
if(f[x][i] != f[y][i]) x = f[x][i], y = f[y][i];
return f[x][0];
}
int lans;
inline void solve_1(){
int x, y, k, lca; scanf("%d%d%d", &x, &y, &k); x ^= lans; y ^= lans; k ^= lans;
lca = get_lca(x, y);
printf("%d
", lans = query(rt[x], rt[y], rt[lca], rt[f[lca][0]], 1, cnt, k));
}
inline void solve_2(){
int x, y, fx, fy; scanf("%d%d", &x, &y); x ^= lans; y ^= lans;
fx = find(x); fy = find(y);
if(sz[fx] < sz[fy]) swap(x, y), swap(fx, fy);
fa[fy] = fx; sz[fx] += sz[fy]; add_edge(x, y); add_edge(y, x); dfs(y, x);
}
int t;
int main(){ memset(head, -1, sizeof head);
scanf("%d", &t); init_hash();
for(int i = 1; i <= n; ++i) fa[i] = i, sz[i] = 1;
for(int i = 1; i <= m; ++i){
int x, y, fx, fy; scanf("%d%d", &x, &y);
add_edge(x, y); add_edge(y, x);
fx = find(x); fy = find(y);
fa[fy] = fx; sz[fx] += sz[fy];
}
for(int i = 1; i <= n; ++i)
if(!vis[i]) dfs(i, -1);
for(int i = 1; i <= k; ++i){
char s[3]; scanf("%s", s);
switch(s[0]){
case 'Q' : solve_1(); break;
case 'L' : solve_2(); break;
}
}
return 0;
}
T14 洛谷 P3293 [SCOI2016]美味
题目描述
一家餐厅有 n 道菜,编号 1...n ,大家对第 i 道菜的评价值为 ai(1<=i<=n)。有 m 位顾客,第 i 位顾客的期望值为 bi,而他的偏好值为 xi 。因此,第 i 位顾客认为第 j 道菜的美味度为 bi XOR (aj+xi),XOR 表示异或运算。
第 i 位顾客希望从这些菜中挑出他认为最美味的菜,即美味值最大的菜,但由于价格等因素,他只能从第 li 道到第 ri 道中选择。请你帮助他们找出最美味的菜。
输入输出格式
输入格式:
第1行,两个整数,n,m,表示菜品数和顾客数。
第2行,n个整数,a1,a2,...,an,表示每道菜的评价值。
第3至m+2行,每行4个整数,b,x,l,r,表示该位顾客的期望值,偏好值,和可以选择菜品区间。
输出格式:
输出 m 行,每行 1 个整数,ymax ,表示该位顾客选择的最美味的菜的美味值。
输入输出样例
输入样例#1:
4 4
1 2 3 4
1 4 1 4
2 3 2 3
3 2 3 3
4 1 2 4
输出样例#1:
9
7
6
7
说明
对于所有测试数据,1<=n<=2*105,0<=ai,bi,xi<105,1<=li<=ri<=n(1<=i<=m);1<=m<=10^5
思路:首先只是个异或,那么一定是要每一位分开讨论的。考虑使 bi XOR (aj+xi) 最大,那么可以贪心的从最高位开始确定。考虑已经确定了前 i 位,答案为 ans,不管接下来的每一位是几,ans 一定属于 ([ans,ans+(1<<i+1)-1])。如果下一位 b 是 0,先考虑能不能选 1,即是否有 a[l]~a[r] 属于 ([ans - x,ans-x+(1<<i)-1]),如果下一位 b 是 1,先考虑能不能选 0,即是否有 a[l]~a[r] 属于 ([ans-x+(1<<i),ans-x+(1<<i+1)-1]),每次区间缩小一半,最后一定能锁定一个 a[i]。
关于判断 a[l]~a[r] 是否属于一个区间,主席树即可实现
#include<iostream>
#include<cstdio>
#define maxn 200010
using namespace std;
int n, m;
#define lc T[i].ch[0]
#define rc T[i].ch[1]
#define Lc T[j].ch[0]
#define Rc T[j].ch[1]
struct zhuxi{
int v, ch[2];
}T[maxn * 20]; int top, rt[maxn];
inline void update(int &i, int j, int l, int r, int k, int v){
i = ++top;
T[i] = T[j]; T[i].v += v;
if(l == r) return ; int m = l + r >> 1;
if(k <= m) update(lc, Lc, l, m, k, v);
else update(rc, Rc, m + 1, r, k, v);
}
int query(int i, int j, int l, int r, int L, int R){
if(l > R || r < L) return 0;
if(L <= l && r <= R) return T[j].v - T[i].v;
int m = l + r >> 1;
return query(lc, Lc, l, m, L, R) + query(rc, Rc, m + 1, r, L, R);
}
int main(){
scanf("%d%d", &n, &m);
for(int i = 1, x; i <= n; ++i){scanf("%d", &x); update(rt[i], rt[i - 1], 1, n, x, 1);}
for(int i = 1; i <= m; ++i){
int b, x, l, r, ans = 0; scanf("%d%d%d%d", &b, &x, &l, &r);
for(int j = 17; j >= 0; --j){
if((b & (1 << j)) && !query(rt[l - 1], rt[r], 1, n, ans - x, ans - x + (1 << j) - 1)) ans += (1 << j);
else if(!(b & (1 << j)) && query(rt[l - 1], rt[r], 1, n, ans - x + (1 << j), ans - x + (1 << j + 1) - 1)) ans += (1 << j);
}
printf("%d
", ans ^ b);
}
return 0;
}
T15 洛谷 P2468 [SDOI2010]粟粟的书架
题目描述
幸福幼儿园B29班的粟粟是一个聪明机灵、乖巧可爱的小朋友,她的爱好是画画和读书,尤其喜欢Thomas H. Cormen的文章。粟粟家中有一个R行C列的巨型书架,书架的每一个位置都摆有一本书,上数第i行、左数第j列摆放的书有Pi,j页厚。
粟粟每天除了读书之外,还有一件必不可少的工作就是摘苹果,她每天必须摘取一个指定的苹果。粟粟家果树上的苹果有的高、有的低,但无论如何凭粟粟自己的个头都难以摘到。不过她发现,如果在脚下放上几本书,就可以够着苹果;她同时注意到,对于第i天指定的那个苹果,只要她脚下放置书的总页数之和不低于Hi,就一定能够摘到。
由于书架内的书过多,父母担心粟粟一天内就把所有书看完而耽误了上幼儿园,于是每天只允许粟粟在一个特定区域内拿书。这个区域是一个矩形,第i天给定区域的左上角是上数第x1i行的左数第y1i本书,右下角是上数第x2i行的左数第y2i本书。换句话说,粟粟在这一天,只能在这﹙x2i-x1i+1﹚×﹙y2i-y1i+1﹚本书中挑选若干本垫在脚下,摘取苹果。
粟粟每次取书时都能及时放回原位,并且她的书架不会再撤下书目或换上新书,摘苹果的任务会一直持续M天。给出每本书籍的页数和每天的区域限制及采摘要求,请你告诉粟粟,她每天至少拿取多少本书,就可以摘到当天指定的苹果。
输入输出格式
输入格式:
输入文件susu.in第一行是三个正整数R, C, M。
接下来是一个R行C列的矩阵,从上到下、从左向右依次给出了每本书的页数Pi,j。
接下来M行,第i行给出正整数x1i, y1i, x2i, y2i, Hi,表示第i天的指定区域是﹙x1i, y1i﹚与﹙x2i, y2i﹚间的矩形,总页数之和要求不低于Hi。
保证1≤x1i≤x2i≤R,1≤y1i≤y2i≤C。
输出格式:
输出文件susu.out有M行,第i行回答粟粟在第i天时为摘到苹果至少需要拿取多少本书。如果即使取走所有书都无法摘到苹果,则在该行输出“Poor QLW”(不含引号)。
输入输出样例
输入样例#1:
5 5 7
14 15 9 26 53
58 9 7 9 32
38 46 26 43 38
32 7 9 50 28
8 41 9 7 17
1 2 5 3 139
3 1 5 5 399
3 3 4 5 91
4 1 4 1 33
1 3 5 4 185
3 3 4 3 23
3 1 3 3 108
输出样例#1:
6
15
2
Poor QLW
9
1
3
输入样例#2:
1 10 7
14 15 9 26 53 58 9 7 9 32
1 2 1 9 170
1 2 1 9 171
1 5 1 7 115
1 1 1 10 228
1 4 1 4 45704571
1 1 1 1 1
1 7 1 8 16
输出样例#2:
6
7
3
10
Poor QLW
1
2
说明
【数据规模和约定】
对于10%的数据,满足R, C≤10;
对于20%的数据,满足R, C≤40;
对于50%的数据,满足R, C≤200,M≤200,000;
另有50%的数据,满足R=1,C≤500,000,M≤20,000;
对于100%的数据,满足1≤Pi,j≤1,000,1≤Hi≤2,000,000,000。
思路:zz 题。显然要数据分治的。考虑只有一行的情况,要使选的书最小且满足大于 hi,故一定要选高度尽量大的书,并且每次从一个区间里找,故能想到主席树。每次二分权值,表示选大于等于的这个权值的所有书,相当于一个后缀和,主席树显然可以维护,最后再考虑二分出来的这个权值的书是否都要选,然后就没了。
考虑是一个矩阵的情况,发现每次二分之后查询的区间都是一个后缀,且 pij <= 1000,故可以用一个二维前缀和,(f[i][j][k]) 表示前 i 行,前 j 列,大于等于 k 的数的总和,然后和主席树一样二分就好了
#include<iostream>
#include<cstdio>
#include<algorithm>
#define maxn 500010
using namespace std;
int n, m, q;
const int N = 1000;
int read(){
int x = 0; char c = getchar();
while(c < '0' || c > '9') c = getchar();
while(c >= '0' && c <= '9'){x = x * 10 + c - '0'; c = getchar();}
return x;
}
#define lc T[i].ch[0]
#define rc T[i].ch[1]
#define Lc T[j].ch[0]
#define Rc T[j].ch[1]
struct zhuxi{
int v1, ch[2], v2;
}T[maxn * 20]; int top, rt[maxn];
int a[maxn];
void update(int &i, int j, int l, int r, int k){
i = ++top;
T[i] = T[j]; ++T[i].v1; T[i].v2 += k;
if(l == r) return ; int m = l + r >> 1;
if(k <= m) update(lc, Lc, l, m, k);
else update(rc, Rc, m + 1, r, k);
}
int query(int i, int j, int l, int r, int k){
if(l == r) return T[j].v2 - T[i].v2;
int m = l + r >> 1; int v = T[Rc].v2 - T[rc].v2;
if(k <= m) return v + query(lc, Lc, l, m, k);
else return query(rc, Rc, m + 1, r, k);
}
int ask1(int i, int j, int l, int r, int k){
if(l == r) return T[j].v1 - T[i].v1;
int m = l + r >> 1;
if(k <= m) return ask1(lc, Lc, l, m, k);
else return ask1(rc, Rc, m + 1, r, k);
}
int ask2(int i, int j, int l, int r, int k){
if(l == r) return T[j].v1 - T[i].v1;
int m = l + r >> 1; int v = T[Rc].v1 - T[rc].v1;
if(k <= m) return v + ask2(lc, Lc, l, m, k);
else return ask2(rc, Rc, m + 1, r, k);
}
bool pd(int x, int l, int r, int v){
int s = query(rt[l - 1], rt[r], 1, N, x);
return s >= v;
}
void solve_1(){
swap(n, m);
for(int i = 1; i <= n; ++i) a[i] = read();
for(int i = 1; i <= n; ++i) update(rt[i], rt[i - 1], 1, N, a[i]);
for(int i = 1; i <= q; ++i){
int l1, l2, r1, r2, z; l1 = read(); r1 = read(); l2 = read(); r2 = read(); z = read();
int l = 1, r = N, mid, ans = -1;
while(l <= r){
mid = l + r >> 1;
if(pd(mid, r1, r2, z)) l = mid + 1, ans = mid;
else r = mid - 1;
}
if(ans == -1){puts("Poor QLW"); continue;}
int Ans = ask2(rt[r1 - 1], rt[r2], 1, N, ans), v = query(rt[r1 - 1], rt[r2], 1, N, ans);
Ans -= (v - z) / ans;
printf("%d
", Ans);
}
}
int A[210][210], f[210][210][1010], s[210][210][1010];
int pd(int x, int l1, int r1, int l2, int r2){
int s = f[l2][r2][x] - f[l1 - 1][r2][x] - f[l2][r1 - 1][x] + f[l1 - 1][r1 - 1][x];
return s;
}
void solve_2(){
for(int i = 1; i <= n; ++i)
for(int j = 1; j <= m; ++j) A[i][j] = read();
for(int i = 1; i <= n; ++i)
for(int j = 1; j <= m; ++j)
for(int k = 1; k <= N; ++k){
s[i][j][k] = s[i - 1][j][k] + s[i][j - 1][k] - s[i - 1][j - 1][k];
f[i][j][k] = f[i - 1][j][k] + f[i][j - 1][k] - f[i - 1][j - 1][k];
if(A[i][j] >= k) f[i][j][k] += A[i][j], ++s[i][j][k];
}
for(int i = 1; i <= q; ++i){
int l1, l2, r1, r2, z; l1 = read(); r1 = read(); l2 = read(); r2 = read(); z = read();
int l = 1, r = N, mid, ans = -1;
while(l <= r){
mid = l + r >> 1;
if(pd(mid, l1, r1, l2, r2) >= z) l = mid + 1, ans = mid;
else r = mid - 1;
}
if(ans == -1){puts("Poor QLW"); continue;}
int v = pd(ans, l1, r1, l2, r2), Ans = s[l2][r2][ans] - s[l1 - 1][r2][ans] - s[l2][r1 - 1][ans] + s[l1 - 1][r1 - 1][ans];
Ans -= (v - z) / ans;
printf("%d
", Ans);
}
}
int main(){
n = read(); m = read(); q = read();
if(n == 1){solve_1(); return 0;}
solve_2();
return 0;
}
T16 洛谷 P4602 [CTSC2018]混合果汁
题目描述
小 R 热衷于做黑暗料理,尤其是混合果汁。
商店里有 nnn 种果汁,编号为 0,1,⋯,n−10,1,cdots,n-10,1,⋯,n−1 。 iii 号果汁的美味度是 did_idi ,每升价格为 pip_ipi 。小 R 在制作混合果汁时,还有一些特殊的规定,即在一瓶混合果汁中, iii 号果汁最多只能添加 lil_ili 升。
现在有 mmm 个小朋友过来找小 R 要混合果汁喝,他们都希望小 R 用商店里的果汁制作成一瓶混合果汁。其中,第 jjj 个小朋友希望他得到的混合果汁总价格不大于 gjg_jgj ,体积不小于 LjL_jLj 。在上述这些限制条件下,小朋友们还希望混合果汁的美味度尽可能地高,一瓶混合果汁的美味度等于所有参与混合的果汁的美味度的最小值。请你计算每个小朋友能喝到的最美味的混合果汁的美味度。
输入输出格式
输入格式:
输入第一行包含两个正整数 n,mn, mn,m ,表示果汁的种数和小朋友的数量。接下来 nnn 行,每行三个正整数 di,pi,lid_i, p_i, l_idi,pi,li ,表示 iii 号果汁的美味度为 did_idi ,每升价格为 pip_ipi ,在一瓶果汁中的添加上限为 lil_ili 。
接下来 mmm 行依次描述所有小朋友:每行两个数正整数 gj,Ljg_j, L_jgj,Lj 描述一个小朋友,表示他最多能支付 gjg_jgj 元钱,他想要至少 LjL_jLj 升果汁。
输出格式:
对于所有小朋友依次输出:对于每个小朋友,输出一行,包含一个整数,表示他能喝到的最美味的混合果汁的美味度。如果无法满足他的需求,则输出 −1-1−1 。
输入输出样例
输入样例#1:
3 4
1 3 5
2 1 3
3 2 5
6 3
5 3
10 10
20 10
输出样例#1:
3
2
-1
1
说明
对于所有的测试数据,保证 n,m≤100000n, m le 100000n,m≤100000 , 1≤di,pi,li≤105,1≤gj,Lj≤10181 le d_i,p_i,l_i le 10^5, 1 le g_j, L_j le 10^{18}1≤di,pi,li≤105,1≤gj,Lj≤1018 。
测试点编号 n m 其他限制 1,2,3 10 10 无 4,5,6 500 500 无 7,8,9 5000 5000 无 10,11,12 100000 100000 pi=1 13,14,15 100000 100000 li=1l 16,17,18,19,20 100000 100000 无
思路:智障题啊。显然答案满足二分,即能用大于 x 的美味度做出来的话,就一定能用大于 x - 1 的美味度做出来(废话啊)。然后发现这不是栗栗的书架?二分 x 之后选钱尽量少的看能不能凑出制定的数量,显然可以主席树,下标代表价格
#include<iostream>
#include<cstdio>
#include<algorithm>
#define maxn 100010
#define ll long long
using namespace std;
int n, m, Max, cnt;
struct node{
int d, p, l;
friend bool operator < (const node &x, const node &y){return x.d < y.d;}
}a[maxn];
ll read(){
ll x = 0; char c = getchar();
while(c < '0' || c > '9') c = getchar();
while(c >= '0' && c <= '9'){x = x * 10 + c - '0'; c = getchar();}
return x;
}
int bs(int x){
int l = 1, r = n, mid, ans;
while(l <= r){
mid = l + r >> 1;
if(a[mid].d >= x) ans = mid, r = mid - 1;
else l = mid + 1;
}
return ans;
}
#define lc T[i].ch[0]
#define rc T[i].ch[1]
#define Lc T[j].ch[0]
#define Rc T[j].ch[1]
struct zhuxi{
int ch[2]; ll s, v;
}T[maxn * 20]; int top, rt[maxn];
void update(int &i, int j, int l, int r, int k, int v, int s){
i = ++top; T[i] = T[j];
T[i].v += 1ll * v * s; T[i].s += s;
if(l == r) return ; int m = l + r >> 1;
if(k <= m) update(lc, Lc, l, m, k, v, s);
else update(rc, Rc, m + 1, r, k, v, s);
}
ll query(int i, int j, int l, int r, ll k){
if(l == r) return k * l; int m = l + r >> 1;
ll s = T[Lc].s - T[lc].s, v = T[Lc].v - T[lc].v;
if(k <= s) return query(lc, Lc, l, m, k);
else return v + query(rc, Rc, m + 1, r, k - s);
}
ll g, L;
bool pd(int x){
int p = bs(x);
if(T[rt[n]].s - T[rt[p - 1]].s < L) return 0;
if(query(rt[p - 1], rt[n], 1, cnt, L) <= g) return 1;
return 0;
}
int main(){
n = read(); m = read();
for(int i = 1; i <= n; ++i){
a[i].d = read(); a[i].p = read(); a[i].l = read();
Max = max(Max, a[i].d); cnt = max(cnt, a[i].p);
}
sort(a + 1, a + n + 1);
for(int i = 1; i <= n; ++i) update(rt[i], rt[i - 1], 1, cnt, a[i].p, a[i].p, a[i].l);
for(int i = 1; i <= m; ++i){
g = read(); L = read();
int l = 1, r = Max, mid, ans = -1;
while(l <= r){
mid = l + r >> 1;
if(pd(mid)) ans = mid, l = mid + 1;
else r = mid - 1;
}
printf("%d
", ans);
}
return 0;
}
T17 洛谷 P4175 [CTSC2008]网络管理
题目描述
M公司是一个非常庞大的跨国公司,在许多国家都设有它的下属分支机构或部门。为了让分布在世界各地的N个部门之间协同工作,公司搭建了一个连接整个公司的通信网络。该网络的结构由N个路由器和N-1条高速光缆组成。每个部门都有一个专属的路由器,部门局域网内的所有机器都联向这个路由器,然后再通过这个通信子网与其他部门进行通信联络。该网络结构保证网络中的任意两个路由器之间都存在一条直接或间接路径以进行通信。 高速光缆的数据传输速度非常快,以至于利用光缆传输的延迟时间可以忽略。但是由于路由器老化,在这些路由器上进行数据交换会带来很大的延迟。而两个路由器之间的通信延迟时间则与这两个路由器通信路径上所有路由器中最大的交换延迟时间有关。作为M公司网络部门的一名实习员工,现在要求你编写一个简单的程序来监视公司的网络状况。该程序能够随时更新网络状况的变化信息(路由器数据交换延迟时间的变化),并且根据询问给出两个路由器通信路径上延迟第k大的路由器的延迟时间。
【任务】 你的程序从输入文件中读入N个路由器和N-1条光缆的连接信息,每个路由器初始的数据交换延迟时间Ti,以及Q条询问(或状态改变)的信息。并依次处理这Q条询问信息,它们可能是:
- 由于更新了设备,或者设备出现新的故障,使得某个路由器的数据交换延迟时间发生了变化。
- 查询某两个路由器a和b之间的路径上延迟第k大的路由器的延迟时间。
输入输出格式
输入格式:
第一行为两个整数N和Q,分别表示路由器总数和询问的总数。
第二行有N个整数,第i个数表示编号为i的路由器初始的数据延迟时间Ti。
紧接着N-1行,每行包含两个整数x和y。表示有一条光缆连接路由器x和路由器y。
紧接着是Q行,每行三个整数k、a、b。
如果k=0,则表示路由器a的状态发生了变化,它的数据交换延迟时间由Ta变为b。
如果k>0,则表示询问a到b的路径上所经过的所有路由器(包括a和b)中延迟第k大的路由器的延迟时间。注意a可以等于b,此时路径上只有一个路由器。
输出格式
对于每一个第二种询问(k>0),输出一行。包含一个整数为相应的延迟时间。如果路径上的路由器不足k个,则输出信息“invalid request!”(全部小写不包含引号,两个单词之间有一个空格)。
输入输出样例
输入样例#1:
5 5
5 1 2 3 4
3 1
2 1
4 3
5 3
2 4 5
0 1 2
2 2 3
2 1 4
3 3 5
输出样例#1:
3
2
2
invalid request!
说明
测试数据满足N,Q<=80000,任意一个路由器在任何时刻都满足延迟时间小于10^8。对于所有询问满足0<=K<=N 。
思路:我们发现只是带修的树链上的第 k 大。树状数组套主席树。每次修改是改一个区间,每次查询是单点查询,所以差分一下就好
#include<iostream>
#include<cstdio>
#include<cctype>
#include<cstring>
#include<algorithm>
#include<cmath>
#define maxn 80010
#define maxm 80010
#define gc() getchar()
using namespace std;
int n, m;
int read(){
int x = 0, f = 1; char c = gc();
while(!isdigit(c)){if(c == '-') f = -1; c = gc();}
while(isdigit(c)){x = x * 10 + c - '0'; c = gc();}
return x * f;
}
struct Edge{
int to, next;
}e[maxn * 2]; int c6, head[maxn];
inline void add_edge(int u, int v){
e[c6].to = v; e[c6].next = head[u]; head[u] = c6++;
}
struct Query{
int opt, x, y;
}Q[maxm];
int id[maxn], c7, sz[maxn], dep[maxn], f[maxn][21];
void dfs(int u, int fa){
id[u] = ++c7; sz[u] = 1;
for(int i = head[u]; ~i; i = e[i].next){
int v = e[i].to; if(v == fa) continue;
dep[v] = dep[u] + 1; f[v][0] = u;
dfs(v, u); sz[u] += sz[v];
}
}
void init_lca(){
for(int j = 1; j <= 20; ++j)
for(int i = 1; i <= n; ++i) f[i][j] = f[f[i][j - 1]][j - 1];
}
int get_lca(int x, int y){
if(dep[x] < dep[y]) swap(x, y);
for(int i = 20; i >= 0; --i)
if(dep[f[x][i]] >= dep[y]) x = f[x][i];
if(x == y) return x;
for(int i = 20; i >= 0; --i)
if(f[x][i] != f[y][i]) x = f[x][i], y = f[y][i];
return f[x][0];
}
inline int _D(int x, int y){
int lca = get_lca(x, y);
return dep[x] + dep[y] - dep[lca] - dep[f[lca][0]];
}
int a[maxn], b[maxn * 2], cnt, c5;
void init_hash(){ c5 = n;
for(int i = 1; i <= n; ++i) b[i] = a[i] = read();
for(int i = 1; i < n; ++i){
int x = read(), y = read();
add_edge(x, y); add_edge(y, x);
}
for(int i = 1; i <= m; ++i){
Q[i].opt = read();
Q[i].x = read(); Q[i].y = read();
if(!Q[i].opt) b[++c5] = Q[i].y;
}
sort(b + 1, b + c5 + 1); cnt = unique(b + 1, b + c5 + 1) - b - 1;
}
inline int get_pos(int x){return lower_bound(b + 1, b + cnt + 1, x) - b;}
#define lc T[i].ch[0]
#define rc T[i].ch[1]
#define Lc T[j].ch[0]
#define Rc T[j].ch[1]
struct zhuxi{
int v, ch[2];
}T[40000010]; int top, rt[maxn];
void update(int &i, int j, int l, int r, int k, int v){
if(!i) i = ++top; T[i] = T[j]; T[i].v += v;
if(l == r) return ; int m = l + r >> 1;
if(k <= m) update(lc, Lc, l, m, k, v);
else update(rc, Rc, m + 1, r, k, v);
}
int A[maxn], B[maxn], C[maxn], D[maxn], c1, c2, c3, c4;
int query(int l, int r, int k){
if(l == r) return b[l]; int v = 0, m = l + r >> 1;
for(int i = 1; i <= c1; ++i) v += T[T[A[i]].ch[0]].v;
for(int i = 1; i <= c2; ++i) v += T[T[B[i]].ch[0]].v;
for(int i = 1; i <= c3; ++i) v -= T[T[C[i]].ch[0]].v;
for(int i = 1; i <= c4; ++i) v -= T[T[D[i]].ch[0]].v;
if(k <= v){
for(int i = 1; i <= c1; ++i) A[i] = T[A[i]].ch[0];
for(int i = 1; i <= c2; ++i) B[i] = T[B[i]].ch[0];
for(int i = 1; i <= c3; ++i) C[i] = T[C[i]].ch[0];
for(int i = 1; i <= c4; ++i) D[i] = T[D[i]].ch[0];
return query(l, m, k);
}
else{
for(int i = 1; i <= c1; ++i) A[i] = T[A[i]].ch[1];
for(int i = 1; i <= c2; ++i) B[i] = T[B[i]].ch[1];
for(int i = 1; i <= c3; ++i) C[i] = T[C[i]].ch[1];
for(int i = 1; i <= c4; ++i) D[i] = T[D[i]].ch[1];
return query(m + 1, r, k - v);
}
}
inline int lowbit(int x){return x & -x;}
void add(int i, int k, int v){
k = get_pos(k);
while(i <= n){update(rt[i], rt[i], 1, cnt, k, v); i += lowbit(i);}
}
inline void solve_1(int i){
int x = Q[i].x, y = Q[i].y;
add(id[x], a[x], -1); add(id[x] + sz[x], a[x], 1);
a[x] = y;
add(id[x], a[x], 1); add(id[x] + sz[x], a[x], -1);
}
inline void solve_2(int i){
int x = Q[i].x, y = Q[i].y, k = Q[i].opt, lca = get_lca(x, y), flca = f[lca][0];
if(k > _D(x, y)){puts("invalid request!"); return ;}
c1 = c2 = c3 = c4 = 0; k = _D(x, y) - k + 1;
for(int j = id[x]; j; j -= lowbit(j)) A[++c1] = rt[j];
for(int j = id[y]; j; j -= lowbit(j)) B[++c2] = rt[j];
for(int j = id[lca]; j; j -= lowbit(j)) C[++c3] = rt[j];
for(int j = id[flca]; j; j -= lowbit(j)) D[++c4] = rt[j];
printf("%d
", query(1, cnt, k));
}
int main(){ memset(head, -1, sizeof head);
n = read(); m = read(); init_hash();
dep[1] = 1; dfs(1, 0); init_lca();
for(int i = 1; i <= n; ++i){
add(id[i], a[i], 1);
add(id[i] + sz[i], a[i], -1);
}
for(int i = 1; i <= m; ++i){
int opt = Q[i].opt;
if(!opt) solve_1(i);
else solve_2(i);
}
return 0;
}
T18 洛谷 P2839 [国家集训队]middle
题目背景
原《畅通工程》见1536
题目描述
一个长度为n的序列a,设其排过序之后为b,其中位数定义为b[n/2],其中a,b从0开始标号,除法取下整。
给你一个长度为n的序列s。
回答Q个这样的询问:s的左端点在[a,b]之间,右端点在[c,d]之间的子序列中,最大的中位数。
其中a<b<c<d。
位置也从0开始标号。
我会使用一些方式强制你在线。
输入输出格式
输入格式:
第一行序列长度n。
接下来n行按顺序给出a中的数。
接下来一行Q。
然后Q行每行a,b,c,d,我们令上个询问的答案是x(如果这是第一个询问则x=0)。
令数组q={(a+x)%n,(b+x)%n,(c+x)%n,(d+x)%n}。
将q从小到大排序之后,令真正的要询问的a=q[0],b=q[1],c=q[2],d=q[3]。
输入保证满足条件。
输出格式:
Q行依次给出询问的答案。
输入输出样例
输入样例#1:
5
170337785
271451044
22430280
969056313
206452321
3
3 1 0 2
2 3 1 4
3 1 4 0
输出样例#1:
271451044
271451044
969056313
说明
0:n,Q<=100
1,...,5:n<=2000
0,...,19:n<=20000,Q<=25000
思路:真正的 二分 + 主席树。
考虑二分答案,把大于等于它的数设置成 1, 小于的设置成 -1。如果区间和大于等于 0,则说明中位数大于等于 x。
([a, b]) 求最大后缀和, ([c,d]) 求最大前缀和, ([b+1,c-1]) 求和,加起来如果如果大于等于 0,则说明可以更大,否则要变小。
可以利用主席树的性质存储每个数二分时的 1/-1 序列。将数组排序后可以直接继承。
复杂度 (O(n*log_2^2n))
#include<iostream>
#include<cstdio>
#include<algorithm>
#define maxn 20010
#define maxm 25010
#define INF 100000000
using namespace std;
int n, m;
struct node{
int v, id;
friend bool operator < (node x, node y){return x.v < y.v;}
}a[maxn]; int b[maxn];
#define lc T[i].ch[0]
#define rc T[i].ch[1]
#define Lc T[j].ch[0]
#define Rc T[j].ch[1]
struct zhuxi{
int v, ch[2], suf, pre;
zhuxi(int _v = 0, int ch1 = 0, int ch2 = 0, int _suf = 0, int _pre = 0){
v = _v; ch[0] = ch1; ch[1] = ch2;
suf = _suf; pre = _pre;
}
}T[maxn * 20]; int top, rt[maxn];
inline void maintain(int i){
T[i].v = T[lc].v + T[rc].v;
T[i].suf = max(T[rc].suf, T[lc].suf + T[rc].v);
T[i].pre = max(T[lc].pre, T[rc].pre + T[lc].v);
}
void build(int &i, int l, int r){
i = ++top;
if(l == r){T[i].v = T[i].suf = T[i].pre = 1; return ;}
int m = l + r >> 1;
build(lc, l, m); build(rc, m + 1, r);
maintain(i);
}
void update(int &i, int j, int l, int r, int k){
i = ++top; lc = Lc; rc = Rc;
if(l == r){T[i].suf = T[i].pre = T[i].v = -1; return ;}
int m = l + r >> 1;
if(k <= m) update(lc, Lc, l, m, k);
else update(rc, Rc, m + 1, r, k);
maintain(i);
}
int q_sum(int i, int l, int r, int L, int R){
if(l > R || r < L) return 0;
if(L <= l && r <= R) return T[i].v;
int m = l + r >> 1;
return q_sum(lc, l, m, L, R) + q_sum(rc, m + 1, r, L, R);
}
zhuxi q_suf(int i, int l, int r, int L, int R){
if(l > R || r < L) return zhuxi(0, 0, 0, -INF, -INF);
if(L <= l && r <= R) return T[i];
int m = l + r >> 1; zhuxi t, t1, t2;
t1 = q_suf(lc, l, m, L, R); t2 = q_suf(rc, m + 1, r, L, R);
t.suf = max(t2.suf, t1.suf + t2.v);
t.v = t1.v + t2.v;
return t;
}
zhuxi q_pre(int i, int l, int r, int L, int R){
if(l > R || r < L) return zhuxi(0, 0, 0, -INF, -INF);
if(L <= l && r <= R) return T[i];
int m = l + r >> 1; zhuxi t, t1, t2;
t1 = q_pre(lc, l, m, L, R); t2 = q_pre(rc, m + 1, r, L, R);
t.pre = max(t1.pre, t2.pre + t1.v);
t.v = t1.v + t2.v;
return t;
}
int c[10], lans;
inline void change(int &l1, int &r1, int &l2, int &r2){
l1 = (l1 + lans) % n; r1 = (r1 + lans) % n; l2 = (l2 + lans) % n; r2 = (r2 + lans) % n;
c[1] = l1; c[2] = r1; c[3] = l2; c[4] = r2;
sort(c + 1, c + 5);
l1 = c[1] + 1; r1 = c[2] + 1; l2 = c[3] + 1; r2 = c[4] + 1;
}
int main(){
cin >> n;
for(int i = 1; i <= n; ++i){
scanf("%d", &a[i].v); b[i] = a[i].v;
a[i].id = i;
}
build(rt[1], 1, n); sort(a + 1, a + n + 1); sort(b + 1, b + n + 1);
for(int i = 2; i <= n; ++i) update(rt[i], rt[i - 1], 1, n, a[i - 1].id);
scanf("%d", &m);
for(int i = 1; i <= m; ++i){
int l1, r1, l2, r2; scanf("%d%d%d%d", &l1, &r1, &l2, &r2);
change(l1, r1, l2, r2);
int l = 1, r = n, mid, ans, v1, v2, v3;
while(l <= r){
mid = l + r >> 1;
if(r1 + 1 <= l2 - 1) v1 = q_sum(rt[mid], 1, n, r1 + 1, l2 - 1);
else v1 = 0;
v2 = q_pre(rt[mid], 1, n, l2, r2).pre;
v3 = q_suf(rt[mid], 1, n, l1, r1).suf;
if(v1 + v2 + v3 >= 0){ans = b[mid]; l = mid + 1;}
else r = mid - 1;
}
printf("%d
", (lans = ans));
}
return 0;
}