今天模拟赛有一道林克卡特树,完全没有思路
赛后想了一想,不就是求(k+1)条不相交的链,使其权值之和最大嘛,傻了。
有一个最裸的(DP),设(f[i][j][k])表示在以(i)为根的子树中,选了(j)条链,(k=0)表示(i)不在链上,(k=1)表示(i)是链的一端,(k=2)表示(i)在链的中间
这样就随便转移了,就是个(O(nk^2))的树上背包
然后呢,又傻了,这能怎么优化?
我先在这里Orz一下大佬BLUESKY007,没有学过wqs二分,发现了(f)数组关于(k)的单调性,一波二分直接A了 %%%%%%
没错,我们需要用这个单调性来进行优化。据官方题解称,假设你闲着没事,把(k=0-100)的表打了一下,你就会发现这个上凸函数,但是如果并没有闲心,那我们就大胆的猜一下。
当(k)很小的时候,我们肯定先删负权边,这样最大权值和就增大了。当负权边不够用了怎么办,我们就只能开始删正权边,这种情况貌似比较复杂,先来看看正权边删的很多的情况。随着正权边越删越多,最大权值和肯定有一个下降的趋势,这样随着(k)的增大,(f)就呈现出一个先增后减的趋势,也许(f)是一个上凸函数?猜对啦,确实是的
接下来我们需要一个叫wqs二分的优化方法,它经常被用于这样的问题:有(n)个带权物品,用满足一定限制的方法选(m)个,使得其权值和取最值,而且权值和的最值是关于(m)的凸函数。设在取(x)个物品时的权值和为(f(x)),那么(f(x))的图像大概长这个样子:
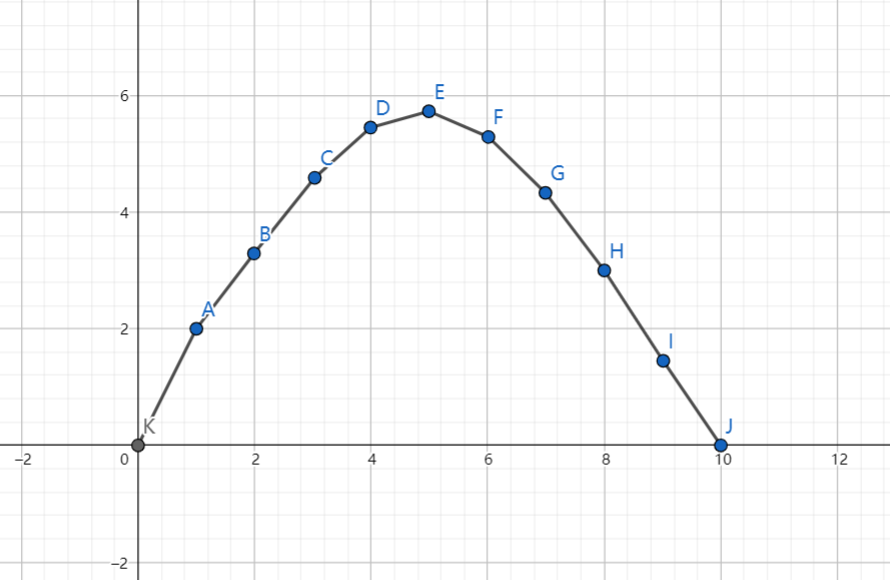
那我们该怎么知道(f(m))呢,因为(f(x))是凸的,考虑用一条直线去切它。就像这样:
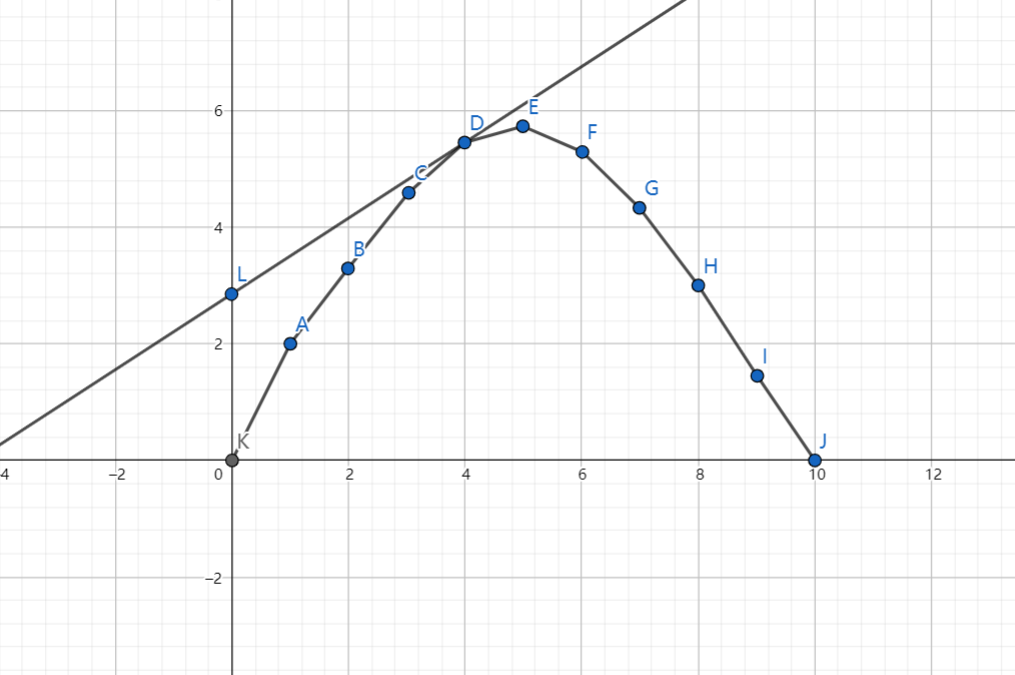
这样我们就得到了一条斜率为(k),解析式为(y=kx+b)的直线,上下移动这条直线,你会发现在切点处的截距(b)是最大的:

而且切点处(b=f(x)-kx),假设我们能找到最大的(b)并顺便记录切点的位置,不就能计算(f(x))的值了吗?观察(b)的表达式,发现如果我们给每个物品加上一个附加权值(-k),然后求出来的最大权值(f'(x))和(f(x)-kx)是等价的,于是(b_{max}=max{f'(x)}),这个式子没有数量限制,直接(DP)就行了,中间顺便记录最佳决策点((x_{max},b_{max}))。这样的话,就能算出来(f(x)=kx_{max}+b_{max})。用因为我们知道了(x_{max}),拿它跟(m)比较,就知道是该增大还是减小斜率(k),这也提示了我们可以二分斜率
还有一个比较重要的细节,就是(b)的最佳决策点可能不止一个,也就是说当前的这条直线跟图像有多个切点,这样我们便无法得知(m)在左边还是右边了。我们可以通过一个策略来解决这个问题,就是取(x)最大的最佳决策点,最后直接把(x_{max})带入求出(f(m))就行了
以下是帮助你取得大师之剑的代码(滑稽):
#include <bits/stdc++.h>
using namespace std;
//dp+wqs二分
//首先把问题转化为求树上k+1条不相交路径,使其权值和最大
#define N 300000
#define ll long long
#define INF 10000000000000 //INF不能太大,也不能太小
int n, k, eid, head[N+5];
ll m;
struct Edge {
int next, to, w;
}e[2*N+5];
struct DP { //为了方便重载了运算符
ll v;
int cnt;
DP operator + (DP rhs) {
return DP{v+rhs.v, cnt+rhs.cnt};
}
bool operator < (DP rhs) const {
return v < rhs.v || (v == rhs.v && cnt < rhs.cnt);
}
}f[3][N+5], temp;
void addEdge(int u, int v, int w) {
e[++eid].next = head[u];
e[eid].to = v;
e[eid].w = w;
head[u] = eid;
}
DP Max(int u) {
return max(f[0][u], max(f[1][u], f[2][u]));
}
DP newDP(DP &a, ll v0, int cnt0) {
return DP{a.v+v0, a.cnt+cnt0};
}
void dp(int u, int fa) {
f[0][u] = DP{0, 0}, f[1][u] = DP{-INF, 0}, f[2][u] = DP{-m, 1};
int i, v, w;
for(i = head[u]; i; i = e[i].next) {
v = e[i].to, w = e[i].w;
if(v == fa) continue;
dp(v, u);
temp = Max(v);
f[2][u] = max(f[2][u]+temp, f[1][u]+max(newDP(f[0][v], w, 0), newDP(f[1][v], w+m, -1)));
f[1][u] = max(f[1][u]+temp, f[0][u]+max(newDP(f[0][v], w-m, +1), newDP(f[1][v], w, 0)));
f[0][u] = f[0][u]+temp;
}
}
void check() {
dp(1, 0);
}
int main() {
scanf("%d%d", &n, &k); k++;
for(int i = 1, x, y, z; i <= n-1; ++i) {
scanf("%d%d%d", &x, &y, &z);
addEdge(x, y, z), addEdge(y, x, z);
}
ll l = -INF, r = INF, ans; //二分斜率
while(l <= r) {
m = (l+r)>>1;
check();
if(Max(1).cnt < k) r = m-1;
else l = m+1, ans = m;
}
m = ans;
check();
printf("%lld
", Max(1).v+ans*k);
return 0;
}
再附一道例题
CF739E. Gosha is hunting
题解在这里