百度百科
泰森多边形又叫冯洛诺伊图(Voronoi diagram),得名于Georgy Voronoi,是由一组由连接两邻点线段的垂直平分线组成的连续多边形组成。
泰森多边形是对空间平面的一种剖分,其特点是多边形内的任何位置离该多边形的样点(如居民点)的距离最近,离相邻多边形内样点的距离远,且每个多边形内含且仅包含一个样点。由于泰森多边形在空间剖分上的等分性特征,因此可用于解决最近点、最小封闭圆等问题,以及许多空间分析问题,如邻接、接近度和可达性分析等。
特征:
- 每个泰森多边形内仅含有一个离散点数据;
- 泰森多边形内的点到相应离散点的距离最近;
- 位于泰森多边形边上的点到其两边的离散点的距离相等。
泰森多边形图例:

详细介绍见百度百科泰森多边形
算法实现
算法一:

算法二:
算法二是基于算法一的优化。本文将着重介绍算法二。
1)算法二同样采用特征点以均匀的速度向外扩张的方式进行。既然我们速度一定,那我们不妨设置为1,那么诸多特征点同时同步地向外扩张,说明在相遇时,相遇的特征点是本着相同的速度,以相同的时间到达的相遇地点(在这里是相遇的单元格),那么根据大众熟知的速度路程公式s=v*t,我们知道这两个相遇的特征点距离该相遇点的路程是相等的,也就是距离一样,说明该相遇点是这两个特征点两线的中点。这就符合了泰森多边形的定义(是由一组由连接两邻点线段的垂直平分线组成的连续多边形组成)
2)扩张的速度我们假定为1,基准的核心点,我们设定为特征点所在像素单元的几何中心。我们规定,在以该特征点为圆心的辐射区域内的其他像素单元格的几何中心距离该特征点所在的几何中心的直线距离(根据勾股定理计算即可)小于或者等于某时间点该特征点以速度为1外扩的半径长度(即路程)时(也就是该像素单元格的大部分面积都包含在该时间点特征点辐射半径所划的圆中的时候),将该像素单元格赋值为特征点外扩运动中此时的时间点信息。
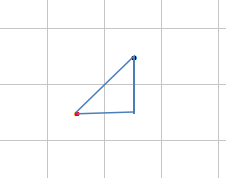
计算中心点:(其中红色点为核心特征点,黑色点为其外扩过程中的一个示例点)
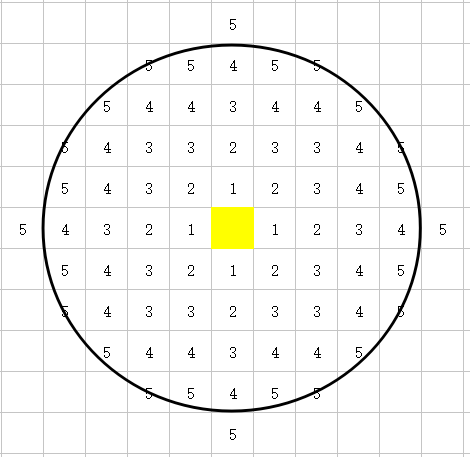
模拟泰森多边形由核心特征点外扩:(单元格中数值代表外扩到该单元格所用的时间)
3)以步骤2)中介绍的方式,我们对所有特征点进行相应外扩,假设每个特征点都辐射满整张矩形区域,共辐射出与特征点数量等量的矩形表数量。(其实可以在代码中把这些特征点辐射的不同数值放在一个数组集合中)。
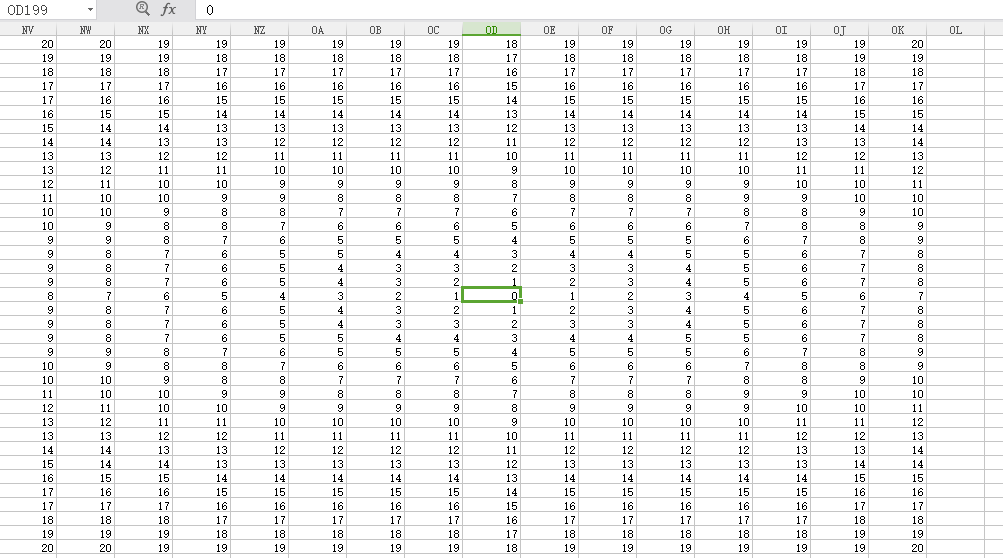
以其中一个特征点辐射满全图为例:(图二是用数值填充满整个矩阵区域后,输出excel,在excel中使用查找替换将相同的数值单元附成相同颜色的背景色)
(注意输出excel时,要输出为“.csv”格式而不是“.xsl”和“.xslx”格式,因为后两种格式有输出行列不超过256的限制,如果你使用矩阵行列小于256,那么就可以使用后两种格式了)
(图一,选中单元即为核心单元点)
(图二,相关查找替换后的模拟图表)
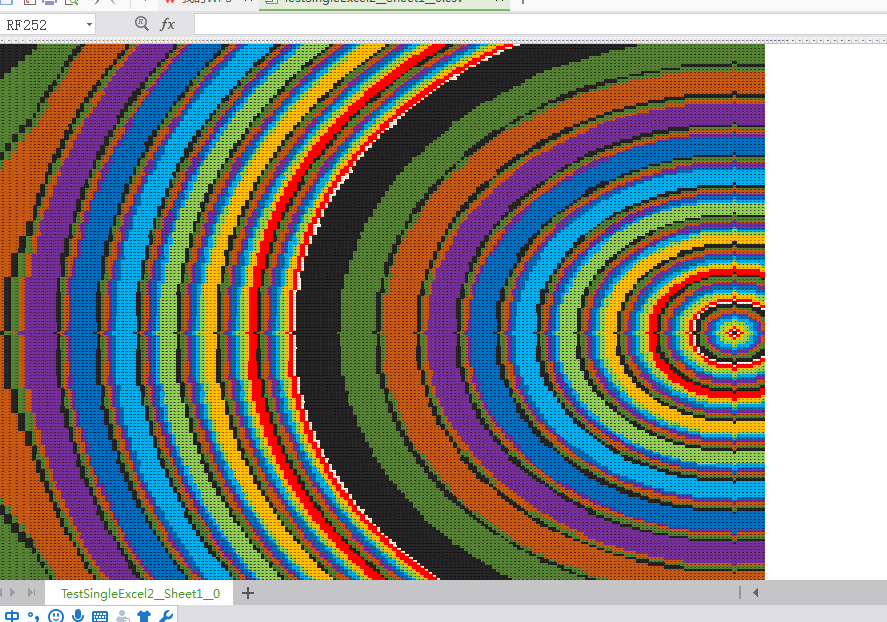
4)依据步骤3)中的操作,我们将所有特征值的辐射全图都计算出后,现在我们依据步骤1)中的理论,当所有的辐射全图中的某个相同单元格中,所有的辐射全图中该单元格赋值有两个并且是最小值相同时,那我们就把它确定为泰森多边形的边界线。
为什么是最小呢?
因为如果两个最近的特征点外延先相遇了,那么后期有人再在此处相遇,对于我们而言就没有什么意义了。
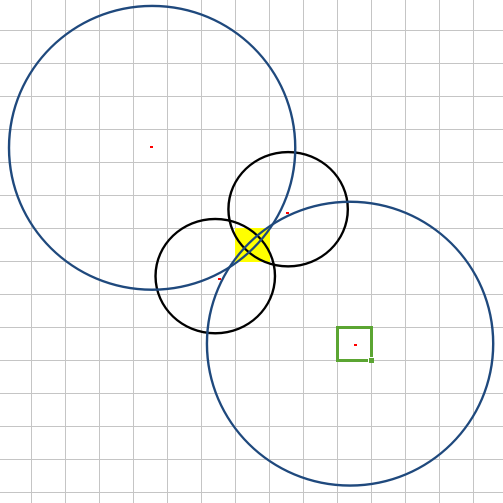
5)现在我们详细说一下步骤2)的某一个特征点扩充到全图的具体操作,回到前面看算法一中的描述,我们要在某特征值的周围进行无穷无尽的试探,以及对于边界单元两边的各特征点外扩部队彼此试探,互通信息困难的问题,我们对算法一进行了优化,也就是算法二,为了提高效率,也本着一次遍历运算完所有单元的原则,我们使用步骤2)中的理论也就是大众熟知的“勾股定理”,对整个矩阵的单元格进行遍历(事先我们不是已经知道特征点的坐标了么,也就是矩阵中的行列号)。对于计算出来的当前单元格中心到特征点中心的直线距离,我们进行一下处理,如果是整数,我们就直接将此数附与该单元格;如果有小数部分,例如3.4,也就是说时间为3的时候,辐射区域还未到此单元格,时间为4的时候已经超越了该单元格中心点,那么我们就为该单元格附上4,也就是对于小数取整加一。
代码实例(python):
小编拿到的初始特征点坐标文件为“xsl”文件,如下:
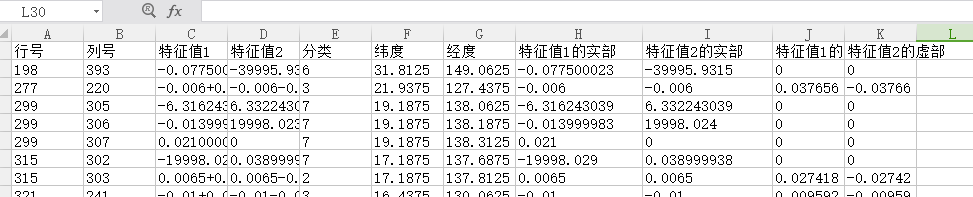
共29个特征点。
我们用到的矩阵大小为533*401。
我们的目标是对这些特征点进行构造泰森多边形,输出该泰森多边形的excel表和图像文件。
我们的大体流程就是:
- 先将这些特征值分别计算出自身辐射全图,分别为每个矩阵单元附上自身辐射到此处的时间
- 对比某个特定单元格中的29个值,如果其中有两个值相等并且是在这29个值中是最小的,那么我们就设定该单元格为边界区域,附上特定值
- 将上步结果附在一个新矩阵中,用此矩阵进行excel文件和图像的输出
#! /usr/bin/env python #coding=utf-8 #************************************输出图像和excel表 # pyexcel_xls 以 OrderedDict 结构处理数据 from collections import OrderedDict from pyexcel_xls import get_data from pyexcel_xls import save_data import cmath import numpy as np from PIL import Image import math def read_xls_file(): xls_data = get_data(r"C:Users123DesktopVoronoi esult.xlsx") # print("Get data type:", type(xls_data)) #for sheet_n in xls_data.keys(): #print(sheet_n, ":", xls_data[sheet_n]) # print(len(xls_data["Sheet1"])) # print(xls_data["Sheet1"][0]) # print(len(xls_data["Sheet1"][0])) # print(type(xls_data["Sheet1"][0][0])) # print(xls_data["Sheet1"][0][0]) # 获取特征点行列号 VList=[] for i in range(len(xls_data["Sheet1"])): if i==0: continue; list1=[] for j in range(len(xls_data["Sheet1"][i])): if j==0: list1.append(xls_data["Sheet1"][i][j]) if j==1: list1.append(xls_data["Sheet1"][i][j]) VList.append(list1) break; # 打印获取的行列号 # for i in range(len(VList)): # for j in range(len(VList[i])): # print(VList[i][j],end=" ") # print() # 建立栅格矩阵 VMatrix=[None]*533 for i in range(len(VMatrix)): VMatrix[i] = [0]*401 for j in range(401): VMatrix[i][j]=[0]*30 print(type(VMatrix[1][1])) # print(VMatrix) # for i in range(533): # for j in range(401): # VMatrix[i][j].append(0); # print(VMatrix[i][j],end=" ") # print() # 为栅格矩阵附上特征点 sum=0; for i in range(len(VList)): VMatrix[VList[i][0]][VList[i][1]][0]=66666 sum=sum+1 print(sum) #打印一下,共29个点 # VMatrix[col][row+v][1]=v;#右 # VMatrix[col][row-v][1]=v;#左 # VMatrix[col+v][row][1]=v;#下 # VMatrix[col-v][row][1]=v;#上 # 在该矩形区域内进行遍历计算 # for i in range(col-1,col+1): # for j in range(row-1,row+1): # Value2=(i-col)*(i-col)+(j-row)*(j-row) # if i==col&j==row: # continue; # elif abs(cmath.sqrt(Value2))<=v: # VMatrix[i][j][1]=v; # 所谓相同速度不同时间,不就是路程么?计算每个单元距离核心单元的具体距离,以速度为1算。 # 若为整数则保留,若有余数,则舍掉,加一 for k in range(len(VList)): col=VList[k][0] row=VList[k][1] for i in range(len(VMatrix)): for j in range(len(VMatrix[i])): if i==col&j==row: continue; Value2=(i-col)*(i-col)+(j-row)*(j-row) distance=cmath.sqrt(abs(Value2)).real if isinstance(distance,int): VMatrix[i][j][k+1]=distance; else: VMatrix[i][j][k+1]=math.ceil(distance); # 单独提取三维列表中的第三维的30个变量中的一个变量 # 该30个变量中,第一个表示特征点,余下29个为29个特征点以自己为核心匀速向外扩展的层次矩阵 # 在某一个单元内,29个特征点流过的路程值中,如果有最小值不止一个,就说明此处为边界上的一个点 SingleVM=[None]*533 for i in range(len(SingleVM)): SingleVM[i] = [255]*401 for j in range(len(SingleVM)): for k1 in range(len(SingleVM[j])): count=0 #29个数中最小值的计数 minV=999999 for k2 in range(len(VMatrix[j][k1])): if k2==0: continue;#要把第一个元素跳过去,因为第一个元素存储的是特征值 # print(VMatrix[j][k1][k3],end=" ") if VMatrix[j][k1][k2]<minV: minV=VMatrix[j][k1][k2] count=1 elif VMatrix[j][k1][k2]==minV: count=count+1 if count>=2: SingleVM[j][k1]=0;#边界矩阵 # print() for i in range(len(VList)): SingleVM[VList[i][0]][VList[i][1]]=0 # 保存到csv文件 data = OrderedDict() # 添加sheet表 data.update({u"Sheet1": SingleVM}) #打印矩阵 # 保存成xls文件 有256行的限制 # 故存成csv文件 addr=r"C:Users123DesktopVoronoiResultBorder2.csv" save_data(addr, data) #保存成图像输出 data_list=np.asarray(SingleVM) pic=Image.fromarray(data_list.astype(np.uint8)) pic.save(r"C:Users123DesktopVoronoiVoronoi.tif") if __name__ == '__main__': read_xls_file()
结果:
1)excel文件:(由于数值过多,此处只附上将边界单元格替换成红色背景后的一部分表格)

2)图像文件:
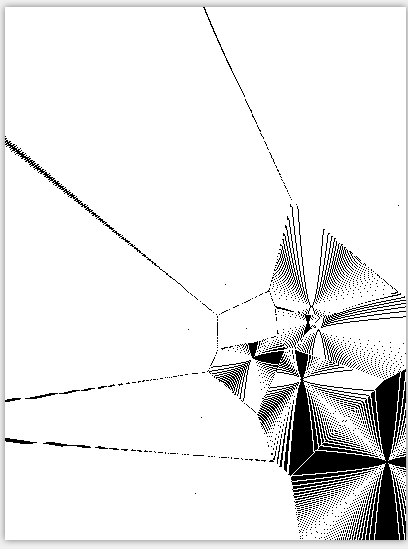
验证代码的正确性:
下面代码,大家可以替换掉开始的VList数组进行运行生成新的泰森多边形。
#! /usr/bin/env python #coding=utf-8 # pyexcel_xls 以 OrderedDict 结构处理数据 # 随便点几点试试 from collections import OrderedDict from pyexcel_xls import get_data from pyexcel_xls import save_data import cmath import numpy as np from PIL import Image import math def read_xls_file(): VList=[[300,200],[100,200],[350,90],[60,80],[150,400]] # 打印获取的行列号 # for i in range(len(VList)): # for j in range(len(VList[i])): # print(VList[i][j],end=" ") # print() # 建立栅格矩阵 VMatrix=[None]*533 for i in range(len(VMatrix)): VMatrix[i] = [0]*401 for j in range(401): VMatrix[i][j]=[0]*6 print(type(VMatrix[1][1])) # print(VMatrix) # for i in range(533): # for j in range(401): # VMatrix[i][j].append(0); # print(VMatrix[i][j],end=" ") # print() # 为栅格矩阵附上特征点 sum=0; for i in range(len(VList)): VMatrix[VList[i][0]][VList[i][1]][0]=0 sum=sum+1 print(sum) #打印一下,共29个点 # VMatrix[col][row+v][1]=v;#右 # VMatrix[col][row-v][1]=v;#左 # VMatrix[col+v][row][1]=v;#下 # VMatrix[col-v][row][1]=v;#上 # 在该矩形区域内进行遍历计算 # for i in range(col-1,col+1): # for j in range(row-1,row+1): # Value2=(i-col)*(i-col)+(j-row)*(j-row) # if i==col&j==row: # continue; # elif abs(cmath.sqrt(Value2))<=v: # VMatrix[i][j][1]=v; # 所谓相同速度不同时间,不就是路程么?计算每个单元距离核心单元的具体距离,以速度为1算。 # 若为整数则保留,若有余数,则舍掉,加一 for k in range(len(VList)): col=VList[k][0] row=VList[k][1] for i in range(len(VMatrix)): for j in range(len(VMatrix[i])): if i==col&j==row: continue; Value2=(i-col)*(i-col)+(j-row)*(j-row) distance=cmath.sqrt(abs(Value2)).real if isinstance(distance,int): VMatrix[i][j][k+1]=distance; else: VMatrix[i][j][k+1]=math.ceil(distance); # 单独提取三维列表中的第三维的30个变量中的一个变量 # 该30个变量中,第一个表示特征点,余下29个为29个特征点以自己为核心匀速向外扩展的层次矩阵 # 在某一个单元内,29个特征点流过的路程值中,如果有最小值不止一个,就说明此处为边界上的一个点 SingleVM=[None]*533 for i in range(len(SingleVM)): SingleVM[i] = [255]*401 for i in range(len(VList)): SingleVM[VList[i][0]][VList[i][1]]=0 for j in range(len(SingleVM)): for k1 in range(len(SingleVM[j])): count=0 #29个数中最小值的计数 minV=999999 for k2 in range(len(VMatrix[j][k1])): if k2==0: continue;#要把第一个元素跳过去,因为第一个元素存储的是特征值 # print(VMatrix[j][k1][k3],end=" ") if VMatrix[j][k1][k2]<minV: minV=VMatrix[j][k1][k2] count=1 elif VMatrix[j][k1][k2]==minV: count=count+1 if count>=2: SingleVM[j][k1]=0;#边界矩阵 # print() # 保存到csv文件 data = OrderedDict() # 添加sheet表 data.update({u"Sheet1": SingleVM}) #打印矩阵 # 保存成xls文件 有256行的限制 # 故存成csv文件 addr=r"C:Users123DesktopVoronoizzshishiBorder2.csv" save_data(addr, data) data_list=np.asarray(SingleVM) pic=Image.fromarray(data_list.astype(np.uint8)) pic.save(r"C:Users123DesktopVoronoizzshishiVoronoi.tif") if __name__ == '__main__': read_xls_file()
本测试代码生成结果: