几种经典排序算法的比较

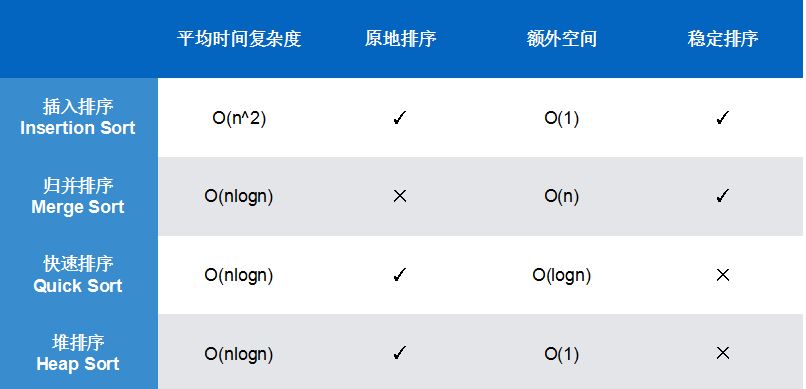
对于时间复杂度来说，快速排序的速度比较快。

一般系统级别的排序都是使用快速排序。对于有可能出现大量重复元素的情况，我们可以使用三路的快速排序。

---

归并排序必须开辟额外的空间完成归并的过程，才能完成归并排序。

快速排序虽然是在原地完成的排序，但它仍然需要log₂n个额外空间。

这是因为我们在使用递归的方式来实现快速排序，需要分成log₂n层，相应地有log₂n层栈空间来保存每一次递归时的临时变量，以供递归返回时继续使用。

同样地，归并也是用递归来实现的，所以它的额外空间应该是O(n+log₂n),只不过n要比log₂n大得多，所以就我们只关注它的额外空间是O（n）级别的。

---

排序算法的稳定性 Stable：对于相等的元素，在排序后，原来靠前的元素依然靠前。相等元素的相对位置没有发生改变。

一些稳定的算法如果实现不好的话依然可能会实现成不稳定的程序。

同时我们还可以使用自定义比较函数，让排序算法不存在稳定性的问题。（其实也就是多比较了一下，相应的会有一些性能损耗）

例如：（在C++中）

bool operator<(const Student& otherStudent){
        
    return score != otherStudent.score ?
               score > otherStudent.score : 
          name < otherStudent.name;

在上表中，我们通常在一个系统级别的排序问题中选择一个稳定的排序算法时，选择归并排序。