from:https://www.sohu.com/a/198093510_783844
前一阵子,某网络公司发起了一个什么建模大赛,有个学员问我,数据建模怎么搞?
为了满足他的好学精神,我决定写这一篇文章,来描述一下数据分析必须要掌握的技能:数据建模。
本文将尝试来梳理一下数据建模的步骤,以及每一步需要做的工作。
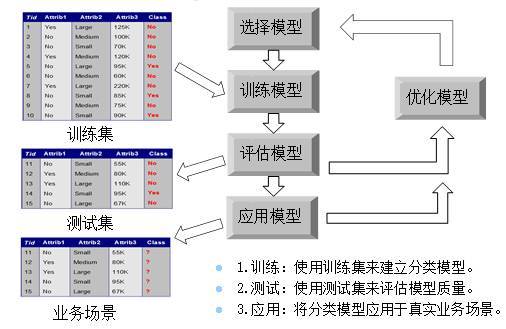
第一步:选择模型或自定义模式
这是建模的第一步,我们需要基于业务问题,来决定可以选择哪些可用的模型。
比如,如果要预测产品销量,则可以选择数值预测模型(比如回归模型,时序预测……);如果要预测员工是否离职,则可以选择分类模型(比如决策树、神经网络……)。
如果没有现成的模型可用,那么恭喜你,你可以自定义模型了。不过,一般情况下,自己定义模型不是那么容易的事情,没有深厚的数学基础和研究精神,自己思考出一个解决特定问题的数学模型基本上是幻想。所以,自定义模型的事情还是留给学校的教授们去研究和开发吧。当前绝大多数人所谓的建模,都只是选择一个已有的数学模型来工作而已。
一般情况,模型都有一个固定的模样和形式。但是,有些模型包含的范围较广,比如回归模型,其实不是某一个特定的模型,而是一类模型。我们知道,所谓的回归模型,其实就是自变量和因变量的一个函数关系式而已,如下表所示。因此,回归模型的选择,也就有了无限的可能性,回归模型的样子(或叫方程)可以是你能够想到的任何形式的回归方程。所以,从某种意义上看,你自己想出一个很少人见过的回归方程,也可以勉强算是自定义模型了哈!
那么,这么多可选的模型,到底选择哪个模型才好呢?
我的答复是:天知道!
天知道应该选择哪个模型会好一些!你问我,我问谁啊?如果在这个时候有人告诉你,你的业务应该选择哪个回归方程会更好一些,那么,我敢肯定,你遇上的肯定是“砖家”而不是“专家”。模型的好坏是不能够单独来评论的(你往下看就知道了)!就如小孩子讨论的你爸爸好还是我爸爸好一样,你说谁好?
那么,是不是我们在选择模型时就得靠运气了?其实真有那么一点靠运气的成份,不过好在后续数学家们给我们提供了评估模型好坏的依据。
现在,我们只能靠运气来选择某一个模型了L。
|
回归模型 |
回归方程 |
|
一元线性 |
y=β0+β1x |
|
多元线性 |
y=β0+β1x1+…+ βkxk |
|
二次曲线 |
y=β0+β1x+β2x2 |
|
复合曲线 |
y=β0βx |
|
增长曲线 |
y=eβ0+β1x |
|
对数曲线 |
y=β0+β1ln(x) |
|
三次曲线 |
y=β0+β1x+β2x2+β3x3 |
|
S曲线 |
y=eβ0+β1/x |
|
指数曲线 |
y=β0eβ1x |
|
逆函数 |
y=β0+β1/x |
|
幂函数 |
y=β0xβ1 |
02
第二步:训练模型
当模型选择好了以后,就到了训练模型这一步。
我们知道,之所以叫模型,这个模型大致的形状或模式是固定的,但模型中还会有一些不确定的东东在里面,这样模型才会有通用性,如果模型中所有的东西都固定死了,模型的通用性就没有了。模型中可以适当变化的部分,一般叫做参数,就比如前面回归模型中的α、β等参数。
所谓训练模型,其实就是要基于真实的业务数据来确定最合适的模型参数而已。模型训练好了,也就是意味着找到了最合适的参数。一旦找到最优参数,模型就基本可用了。
当然,要找到最优的模型参数一般是比较困难的,怎样找?如何找?这就涉及到算法了。哦,一想到算法,我的头就开始痛了,都怪当年数学没有学好呀!
当然,最笨的办法,我们可以不断的尝试参数,来找到一个最好的参数值。一个一个试?这不是要试到生命结束?开玩笑啦,不可能去一个一个试的啦。反正有工具会帮你找到最优参数的,什么最优化算法中的什么梯度上升呀梯度下降呀,你就不用操心了呀,这些留给分析工具来实现就可以了!
当然,一个好的算法要运行速度快且复杂度低,这样才能够实现快速的收敛,而且能够找到全局最优的参数,否则训练所花的时间过长效率低,还只找到局部最优参数,就让人难以忍受了。
03
第三步:评估模型
模型训练好以后,接下来就是评估模型。
所谓评估模型,就是决定一下模型的质量,判断模型是否有用。
前面说过,模型的好坏是不能够单独评估的,一个模型的好坏是需要放在特定的业务场景下来评估的,也就是基于特定的数据集下才能知道哪个模型好与坏。
既然要评估一个模型的好坏,就应该有一些评价指标。比如,数值预测模型中,评价模型质量的常用指标有:平均误差率、判定系数R2,等等;评估分类预测模型质量的常用指标(如下图所示)有:正确率、查全率、查准率、ROC曲线和AUC值等等。
对于分类预测模型,一般要求正确率和查全率等越大越好,最好都接近100%,表示模型质量好,无误判。

在真实的业务场景中,评估指标是基于测试集的,而不是训练集。所以,在建模时,一般要将原始数据集分成两部分,一部分用于训练模型,叫训练集;另一部分用于评估模型,叫测试集或验证集。
有的人可能会想,为什么评估模型要用两个不同的数据集,直接用一个训练集不就可以了?理论上是不行的,因为模型是基于训练集构建起来的,所以在理论上模型在训练集上肯定有较好的效果。但是,后来数学家们发现,在训练集上有较好预测效果的模型,在真实的业务应用场景下其预测效果不一定好(这种现象称之为过拟合)。所以,将训练集和测试集分开来,一个用于训练模型,一个用于评估模型,这样可以提前发现模型是不是存在过拟合。
如果发现在训练集和测试集上的预测效果差不多,就表示模型质量尚好,应该可以直接使用了。如果发现训练集和测试集上的预测效果相差太远,就说明模型还有优化的余地。
当然,如果只想验证一次就想准确评估出模型的好坏,好像是不合适的。所以,建议采用交叉验证的方式来进行多次评估,以找到准确的模型误差。
其实,模型的评估是分开在两个业务场景中的:
一是基于过去发生的业务数据进行验证,即测试集。本来,模型的构建就是基于过去的数据集的构建的。
二是基于真实的业务场景数据进行验证。即,在应用模型步骤中检验模型的真实应用结果。
04
第四步:应用模型
如果评估模型质量在可接受的范围内,而且没有出现过拟合,于是就可以开始应用模型了。
这一步,就需要将可用的模型开发出来,并部署在数据分析系统中,然后可以形成数据分析的模板和可视化的分析结果,以便实现自动化的数据分析报告。
应用模型,就是将模型应用于真实的业务场景。构建模型的目的,就是要用于解决工作中的业务问题的,比如预测客户行为,比如划分客户群,等等。
当然,应用模型过程中,还需要收集业务预测结果与真实的业务结果,以检验模型在真实的业务场景中的效果,同时用于后续模型的优化。
05
第五步:优化模型
优化模型,一般发生在两种情况下:
一是在评估模型中,如果发现模型欠拟合,或者过拟合,说明这个模型待优化。
二是在真实应用场景中,定期进行优化,或者当发现模型在真实的业务场景中效果不好时,也要启动优化。
如果在评估模型时,发现模型欠拟合(即效果不佳)或者过拟合,则模型不可用,需要优化模型。所谓的模型优化,可以有以下几种情况:
1)重新选择一个新的模型;
2)模型中增加新的考虑因素;
3)尝试调整模型中的阈值到最优;
4)尝试对原始数据进行更多的预处理,比如派生新变量。
不同的模型,其模型优化的具体做法也不一样。比如回归模型的优化,你可能要考虑异常数据对模型的影响,也要进行非线性和共线性的检验;再比如说分类模型的优化,主要是一些阈值的调整,以实现精准性与通用性的均衡。
当然,也可以采用元算法来优化模型,就是通过训练多个弱模型,来构建一个强模型(即三个臭皮匠,顶上一个诸葛亮)来实现模型的最佳效果。
实际上,模型优化不仅仅包含了对模型本身的优化,还包含了对原始数据的处理优化,如果数据能够得到有效的预处理,可以在某种程度上降低对模型的要求。所以,当你发现你尝试的所有模型效果都不太好的时候,别忘记了,这有可能是你的数据集没有得到有效的预处理,没有找到合适的关键因素(自变量)。
不可能有一个模型适用于所有业务场景,也不太可能有一个固有的模型就适用于你的业务场景。好模型都是优化出来的!
最后语
正如数据挖掘标准流程一样,构建模型的这五个步骤,并不是单向的,而是一个循环的过程。当发现模型不佳时,就需要优化,就有可能回到最开始的地方重新开始思考。即使模型可用了,也需要定期对模型进行维护和优化,以便让模型能够继续适用新的业务场景。