一. 搜索算法介绍
1. 暴力穷举的思想
2. 搜索是一种通用的解决问题的手段，但复杂度往往较高
二. 基本搜索算法
DFS 与 BFS
三. 优化
1. 爬山法
思想：（局部优化的贪心法 + DFS）
在深度优先搜索过程中, 我们经常遇到多个节点可以扩展的情况, 爬山策略使用贪心方法确定搜索的方向 ， 使用启发式测度来排序节点扩展的顺序。
a. 定义启发式函数：对DFS下一次扩展出的结点，(f(结点) = 到目标的估计距离)
b. 在深度优先扩展结点时，将结点按启发式函数从大到小压入栈
2. Best-first
思想：（全局优化的贪心 + DFS + BFS）
best-first策略结合深度搜索和广度搜索的优点，根据一个评价函数，在目前产生的所有节点中选择具有最小评价函数值的节点来进一步扩展。
a. 评价函数：对所有的结点，(f(结点) = 到目标的估计距离)
b. 根据评价函数构造小顶堆，每次取出堆顶元素进行扩展
3. 分支界限法
注：爬山法和Best-first解决可行解的问题 ，分支界限解决优化解的问题
思想：（可行解 + 剪枝策略 ~> 优化解）
a.设计产生分支（得到问题上界）的机制
b. 剪枝缩小问题规模
分支限界法通过发现优化解的一个界限来缩小解空间，从而提高求解效率。
四. 应用
1. 8-puzzle 问题
- 问题定义
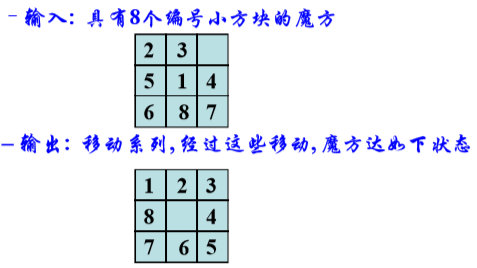
- 如何转化成图上的搜索问题
每个状态看作一个结点，状态的变化看作一条边
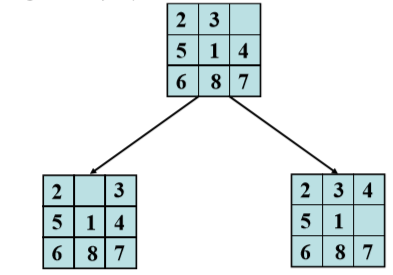
- 算法设计：只需找到从输入结点到输出结点的路径即可
（1）爬山法
a. 设每个结点的启发式函数为与目标结点对比错误的方块数
b. 在深度优先扩展结点时，将结点按启发式函数从大到小压入栈即可。
（2）Best-first
a. 设每个结点的启发式函数为与目标结点对比错误的方块数
b. 将结点构建成最小堆，每次取出堆顶元素进行扩展
2. 布尔表达式问题
- 问题定义：
– 输入: n个布尔变量x1,x2, …., xn 关于x1,x2, …., xn的k个析取布尔式
– 输出: 是否存在一个x1,x2, …., xn的一种赋值 使得所有k个布尔析取式皆为真
- 如何转化成图上的搜索问题
将T/F的问题转化为二叉树
- 算法设计
（1）爬山法/Best-first：
a. 设启发式函数/评价函数为：如果该结点对应的布尔表达式存在假值（f = 0），否则（f = 布尔表达式正确的个数）
3. 哈密顿环问题
- 问题定义
–输入: 具有n个节点的连通图G=(V, E)
– 输出: G中是否具有Hamiltonian环
- 如何转化成图的搜索问题
将任意一个顶点作为根节点，不断扩展与他连通结点构造树
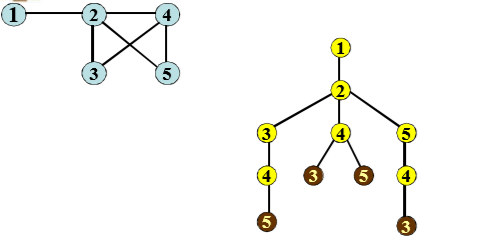
- 算法设计
（1）爬山法/Best-first
设启发式函数/评价函数为：根结点到该结点的距离
4. 子集合和的问题
- 问题定义
输入: S={7, 5, 1, 2, 10}
输出: 是否存在子集S ’ , 使得Sum(S ’ )=9
- 算法设计
（1）动态规划：更适合解最优化的问题（例如：子集合和最大的问题）
（2）搜索算法：通用、解决存在性问题更合适
综上选择搜索算法
- 如何转化成图的搜索问题
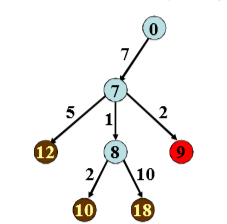---只展示了一个分支
- 启发式函数/评价函数：9 - 当前结点和
5. 多阶段图问题（分支界限）
- 问题定义
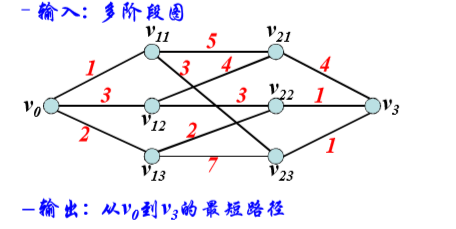
- 问题树表示
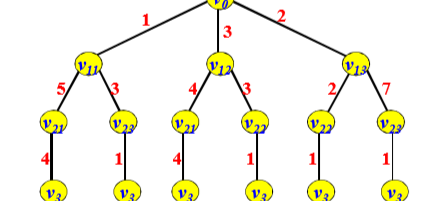
- 算法设计
最优解的设计方案--选择分支界限的方式
a. 使用爬山法得到问题的一个上界
b. 剪枝，缩小解空间
五. 拓展
本篇主要介绍几种搜索的思想，关于分支界限的应用、A*算法将在下一篇中详述