一. 预备知识
1. 流网络:
有向图G=(V,E)满足(1)存在无入边的源结点s(2)存在无出边的目标点t(3)每条边e都有一个非负容量ci
2. 流
流网络中从s-t的流是一个实值函数 f ,满足

3. 余图(残存网络)
对于流网络G,边容量为c,流为f,则定义残存容量cf 为
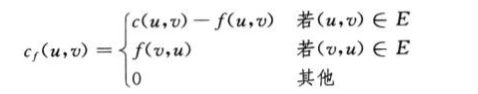
即,对每一条边,正向记为:c - f,逆向记为:f
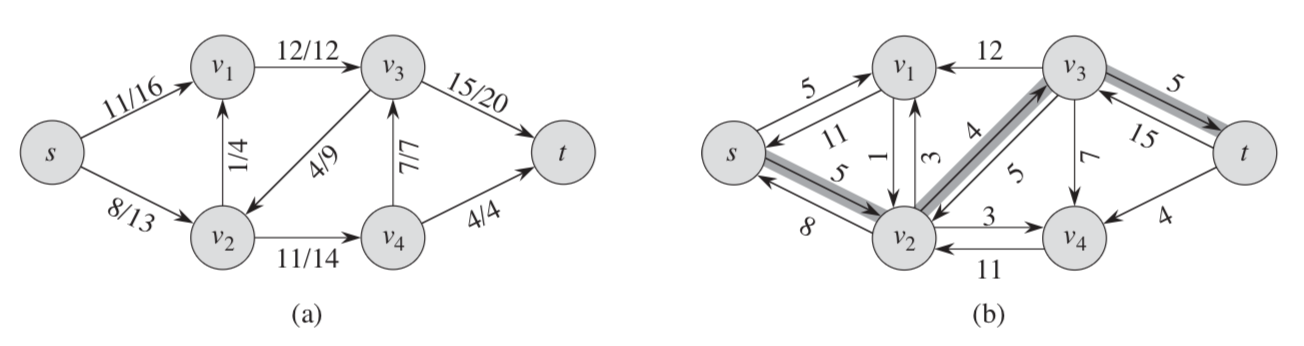
图(a)为一个流网络,图(b)展示了它的余图
4. 增广路径
在余图中找到一条s~>t最大流量的路径,该路径为增广路径
上图(b)中s-v2-v3-t,容量为4的路径即为增广路径
5. 流网络的切割
流网络G中的一个切割(S,T)将结点集合V划分为S和T=V-S两个集合,满足s€S,t€T。
- 切割的净流量:
![]()
- 切割的容量:
![]()
推论:流和割弱对偶关系
给定流网络 G=(V,E),s是源,t是汇. 设f是G上的 一个流,S,T是G的任意一个切割,则f(S,T)=| f |.
给定流网络 G=(V,E). 设f是G上的一个流,S,T 是G的任意一个割,则| f | <= c(S,T)
二.最大流算法(基本的Ford-fulkerson方法)
1. 思路:
(1)初始化:对所有的e,f( e ) = 0
(2)while迭代:
只要G的余图中存在增广路径P,沿着P更新 流 和 余图
直到不存在P
(3) 得到最大流
2. 定理

3. 算法正确性证明
(1)可终止性:不妨将容量放缩,乘一个系数使之成为整数,则每次流至少增加整数1,则可终止
(2)时间复杂度:O(mC),m:边的数量,C:最大流 | f |。
(3)正确性:
设FF算法在流 f 上停止
则,不存在s - t 的路径P,即s 与 t不连通
设:与s连通的点集为S,
则(S,V-S)是G的一个切割
对任意的u€S,v€V-S,f(u,v) = c(u,v)
则| f | = c(S,T)
而| f | <= c(S,T)
则f是最大流。
4. 算法改进:
--算法优劣主要取决于寻找增广路径的时间复杂度
