GSS7解题报告
前言
唔,有点恶心哪,废了两个多小时debug
思路
很容易看出傻子都知道,这个是树链剖分+线段树的裸题,只不过是恶心了点,这里重点讲一下细节问题
线段树
做过GSS系列的都应该很熟悉了
线段树维护的前缀最大子段和,后缀最大子段和,和区间最大子段和
那么我们就可以很容易的写出他合并orpushup
void pushup(node &a,node x,node y) {
a.ans=max(max(x.ans,y.ans),x.rk+y.lk);
a.lk=max(x.sum+y.lk,x.lk);
a.rk=max(y.sum+x.rk,y.rk);
a.sum= x.sum +y.sum;
}
这里写成这种形式对下面的跳链比较友好
查询也是比较套路的 返回一个node,如果在mid两边,再次合并,这里就不多说了
树剖跳链
修改操作:
跳链,修改,和平常一样
查询操作:
x到y的路径是一条链子
如果我们把它伸直,捋平咯,那他就是一串数列
那我们就可以一块一块的合并喽
想一下我们是怎么跳的
是从链的两端跳,一直跳到他们相遇
那我们就维护两端的信息,也就是从起点到现在的x的区间和从现在的y到终点的区间
最后再合并起来,就是整个区间的信息喽
不过要注意合并时候的次序和l,r的交换
也许不swap而分类讨论就没这个东西了吧
我们的一条重链是从浅处到深处依次排列
我们跳的时候是从深处到浅出跳(从两端逼近中间)
所以合并就要考虑清楚了
是合并x,y还是合并y,x
文字说起来不太明白,我举个栗子吧
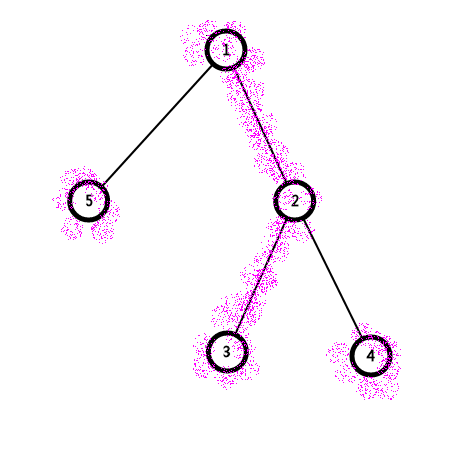
2号权值为-1,其他权值为1,要从4号到5号点
我们先从5号节点跳到1号所属重链
在跳之前我们先查询一下5号的值,得到一个node,和x
合并
我们再从4号节点跳到1号所属重链
在跳之前我们先查询一下4号的值,又得到一个node,和y合并
然后交换x,y(别问我为什么)
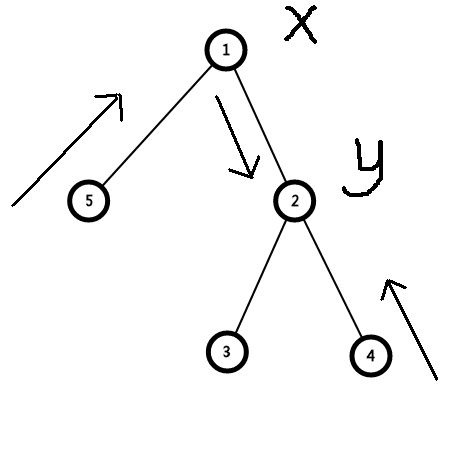
现在x,y都到了一条链子上了(注意前提)
我们考虑一下两端区间的方向
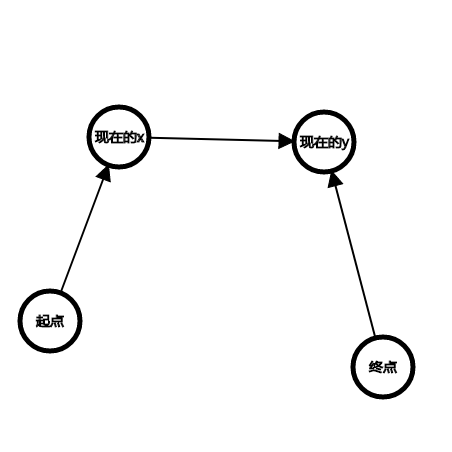
有一个是反着的,我们翻过来其中一个然后全部合并起来就好了
这里给出我的两组简单但易错数据(反正错了我好多次)
5
-1 1 1 1 1
1 5
1 2
2 3
2 4
1
1 4 5
ans=2
5
-3 -2 -1 -2 -3
1 2
2 3
1 4
4 5
2
2 3 4 2
1 2 5
ans=6
代码
#include <bits/stdc++.h>
#define FOR(i,a,b) for(int i=a;i<=b;++i)
using namespace std;
const int N=6e5+7;
const int inf=0x3f3f3f3f;
inline int read() {
int x=0,f=1;char s=getchar();
for(;s>'9'||s<'0';s=getchar()) if(s=='-') f=-1;
for(;s>='0'&&s<='9';s=getchar()) x=x*10+s-'0';
return x*f;
}
vector<int> G[N];
int n,m;
int a[N],w[N],idx[N],top[N],son[N],siz[N],f[N],dep[N],cnt;
inline int max(const int &x,const int &y) {return x>y?x:y;}
void dfs1(int u,int fa) {
f[u]=fa;
siz[u]=1;
dep[u]=dep[fa]+1;
for(std::vector<int>::iterator it=G[u].begin();it!=G[u].end();++it) {
if(fa==*it) continue;
dfs1(*it,u);
siz[u]+=siz[*it];
if(siz[son[u]]<siz[*it]) son[u]=*it;
}
}
void dfs2(int u,int topf) {
idx[u]=++cnt;
a[cnt]=w[u];
top[u]=topf;
if(!son[u]) return;
dfs2(son[u],topf);
for(std::vector<int>::iterator it=G[u].begin();it!=G[u].end();++it)
if(!idx[*it]) dfs2(*it,*it);
}
namespace seg_tree {
#define ls rt<<1
#define rs rt<<1|1
struct node {
int l,r,siz,lk,rk,ans,lazy,sum;
}e[N<<2];
inline void pushup(node &a,node x,node y) {
a.ans=max(max(x.ans,y.ans),x.rk+y.lk);
a.lk=max(x.sum+y.lk,x.lk);
a.rk=max(y.sum+x.rk,y.rk);
a.sum= x.sum +y.sum;
}
void build(int l,int r,int rt) {
e[rt].l=l,e[rt].r=r,e[rt].siz=r-l+1;
e[rt].lazy=inf;
if(l==r) {
e[rt].sum=a[l];
e[rt].lk=e[rt].rk=e[rt].ans=max(a[l],0);
return;
}
int mid=(l+r)>>1;
build(l,mid,ls);
build(mid+1,r,rs);
pushup(e[rt],e[ls],e[rs]);
}
inline void tag(int rt,int k) {
e[rt].sum=e[rt].siz*k;
if(k>=0) e[rt].lk=e[rt].rk=e[rt].ans=e[rt].sum;
else e[rt].lk=e[rt].rk=e[rt].ans=0;
e[rt].lazy=k;
}
inline void pushdown(int rt) {
if(e[rt].lazy!=inf) {
tag(ls,e[rt].lazy);
tag(rs,e[rt].lazy);
e[rt].lazy=inf;
}
}
void modify(int L,int R,int k,int rt) {
if(L<=e[rt].l&&e[rt].r<=R) {
tag(rt,k);
return;
}
pushdown(rt);
int mid=(e[rt].l+e[rt].r)>>1;
if(L<=mid) modify(L,R,k,ls);
if(R>mid) modify(L,R,k,rs);
pushup(e[rt],e[ls],e[rs]);
}
node query(int L,int R,int rt) {
if(L<=e[rt].l&&e[rt].r<=R) return e[rt];
pushdown(rt);
int mid=(e[rt].l+e[rt].r)>>1;
if(L<=mid && R>mid) {
node a=query(L,R,ls),b=query(L,R,rs),c;
pushup(c,a,b);
return c;
}
if(L<=mid) return query(L,R,ls);
if(R>mid) return query(L,R,rs);
}
}
void QQ(int x,int y) {
seg_tree::node tot_x={},tot_y={};
while(top[x]!=top[y]) {
if(dep[top[x]]<dep[top[y]]) swap(x,y),swap(tot_x,tot_y);
seg_tree::node tmp=seg_tree::query(idx[top[x]],idx[x],1);
seg_tree::pushup(tot_x,tmp,tot_x);
x=f[top[x]];
}
if(dep[x]>dep[y]) swap(x,y),swap(tot_x,tot_y);
seg_tree::node tmp=seg_tree::query(idx[x],idx[y],1);
swap(tot_x.lk,tot_x.rk);
seg_tree::pushup(tot_x,tot_x,tmp);
seg_tree::pushup(tot_y,tot_x,tot_y);
printf("%d
",tot_y.ans);
}
void CC(int x,int y,int c) {
while(top[x]!=top[y]) {
if(dep[top[x]]<dep[top[y]]) swap(x,y);
seg_tree::modify(idx[top[x]],idx[x],c,1);
x=f[top[x]];
}
if(dep[x]>dep[y]) swap(x,y);
seg_tree::modify(idx[x],idx[y],c,1);
}
int main() {
n=read();
FOR(i,1,n) w[i]=read();
FOR(i,2,n) {
int x=read(),y=read();
G[x].push_back(y);
G[y].push_back(x);
}
dfs1(1,0);
dfs2(1,1);
seg_tree::build(1,n,1);
m=read();
FOR(i,1,m) {
int opt=read(),x=read(),y=read(),z;
if(opt==1) QQ(x,y);
else z=read(),CC(x,y,z);
}
return 0;
}