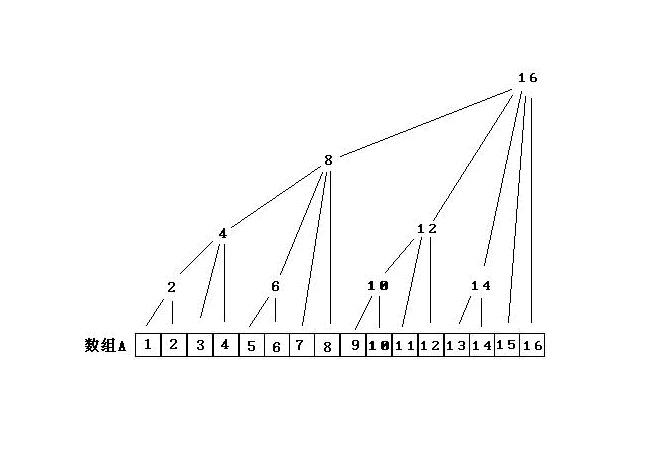
分析一下上面那个图看能得出什么规律:
据图可知:c1=a1,c2=a1+a2,c3=a3,c4=a1+a2+a3+a4,c5=a5,c6=a5+a6,c7=a7,c8=a1+a2+a3+a4+a5+a6+a7+a8,c9=a9,c10=a9+a10,c11=a11........c16=a1+a2+a3+a4+a5+.......+a16。
分析上面的几组式子可知,当 i 为奇数时,ci=ai ;当 i 为偶数时,就要看 i 的因子中最多有二的多少次幂,例如,6 的因子中有 2 的一次幂,等于 2 ,所以 c6=a5+a6(由六向前数两个数的和),4 的因子中有 2 的两次幂,等于 4 ,所以 c4=a1+a2+a3+a4(由四向前数四个数的和)。
int c[50005],n; //c为数状数组,n为该书组长度
int lowbit(int x) //数组下标变化 { return x&-x; } void add(int i,int j)//c[i]~c[n]都加j { while(i<=n) { c[i]+=j; i+=lowbit(i); } } int sum(int i)//求c[0]~c[i]的和 { int sums=0; while(i>0) { sums+=c[i]; i-=lowbit(i); } return sums; }