#include<bits/stdc++.h> using namespace std; const int maxn=1010; #define inf 0x3fffffff int Next[maxn]; string s1,s2; int m,n; void buildNext(){ Next[0]=-1; int i; for(int j=1;j<m;j++){ i=Next[j-1];//存储最大前缀的最后一个值的下标 while((i>=0)&&(s2[i+1]!=s2[j])){//若当前前缀不符合,则回退,找寻次大的前缀 i=Next[i]; } if(s2[i+1]==s2[j]){ Next[j]=i+1; } else{//i<0,不存在前缀 Next[j]=-1; } } } int main(){ cin>>s1>>s2; n=s1.length(); m=s2.length(); buildNext(); int i=0,j=0; while(i<n&&j<m){ if(s1[i]==s2[j]){ i++; j++; } else if(j>0){ j=Next[j-1]+1; } else{ i++; } } if(j==m){ cout<<i-m<<endl; } else{ cout<<-1<<endl; } return 0; }
理解:
KMP思想:配对不成功时,将最大前缀与后缀对齐,从而减少匹配次数。
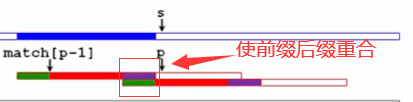
next数组的作用:配对不成功时,子串指针移动到最大前缀的最后一个值的下一个位置,就是next的值。
int buildNext(){ Next[0]=-1; int i; for(int j=1;j<m;j++){ i=Next[j-1];//存储最大前缀的最后一个值的下标 while((i>=0)&&(s2[i+1]!=s2[j])){//若当前前缀不符合,则回退,找寻次大的前缀 i=Next[i]; } if(s2[i+1]==s2[j]){ Next[j]=i+1; } else{//i<0,不存在前缀 Next[j]=-1; } } }
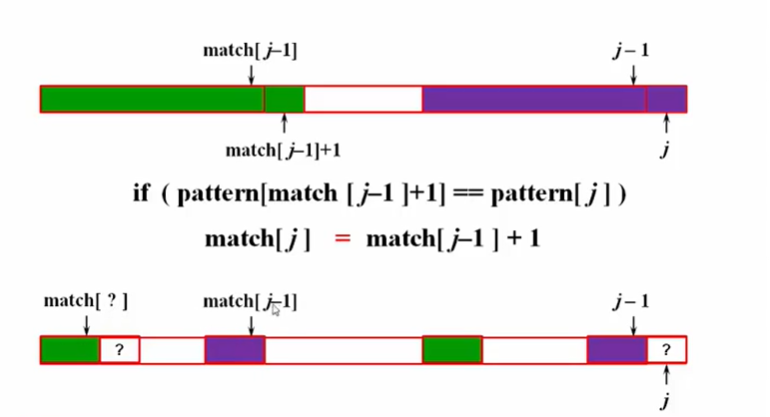
递推方式求解next,如下图:如果在j-1配对的基础上,如果match[j-1]+1与j的字符相等,则可以直接:match[j]=match[j-1]+1 (可以通过反证法证明)
如果不相等,则讲 i 回退,找次小的前缀。while里面是前缀递减的过程