TIPS:数据包下载(NOI官网)
P5019 铺设道路
题目
思路
一道水题
对于每段区间[l,r]最小值为minn,所有di (i∈[l,r])-=minn
ans += minn
以每一个为0的d[i]作为分割点递归即可
代码
#include <iostream>
#include <cstdio>
#include <algorithm>
using namespace std;
int read(){
int re = 0 , sig = 1;
char c = getchar();
while(c < '0' || c > '9'){
if(c == '-')sig = -1;
c = getchar();
}
while(c >= '0' && c <= '9'){
re = (re << 1) + (re << 3) + c - '0';
c = getchar();
}
return re * sig;
}
int n;
int d[100010];
int ans;
void dfs(int l , int r){
// cout << l << ' ' << r << endl;
if(l > r)return;
int minn = (1 << 29) , k = -1;
for(int i = l ; i <= r ; i++){
if(minn > d[i])
minn = d[i] , k = i;
}
ans += minn;
for(int i = l ; i <= r ; i++)
d[i] -= minn;
int las = l;
for(int i = l ; i <= r ; i++){
if(d[i] == 0){
dfs(las , i - 1);
las = i + 1;
}
}
dfs(las , r);
}
int main(){
n = read();
for(int i = 1 ; i <= n ; i++)
d[i] = read();
dfs(1 , n);
cout << ans;
return 0;
}
P5020 货币系统
题目
思路
又一道水题
对于每个a[i]若它可以表示为
则a[i]在货币系统中可有可无,根据题意,不统计它即可,显然,所有的a[j]都是小于等于a[i]的。因此,我们可以将a从小到大数组排序,用类似无限背包的思想解决:设f[i]表示面值为i的货币是否可以被表示(false不能,true可以)初始化f[0]=true,当f[a[i]]=false时,a[i]不能被系统中的其他货币表示出来,统计a[i] (ans++)并用a[i]跑一边无限背包
代码
#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
using namespace std;
int read(){
int re = 0 , sig = 1;
char c = getchar();
while(c < '0' || c > '9'){
if(c == '-')sig = -1;
c = getchar();
}
while(c >= '0' && c <= '9'){
re = (re << 1) + (re << 3) + c - '0';
c = getchar();
}
return re * sig;
}
int n , sum;
int a[110];
bool f[25010];
int main(){
int T = read();
while(T--){
memset(f , 0 , sizeof(f));
f[0] = true;
sum = 0;
n = read();
for(int i = 1 ; i <= n ; i++)
a[i] = read();
sort(a + 1 , a + n + 1);
for(int i = 1 ; i <= n ; i++){
if(f[a[i]])continue;
sum++;
for(int j = 0 ; j <= a[n] - a[i] ; j ++)
if(f[j])
f[j + a[i]] = true;
}
printf("%d
" , sum);
}
return 0;
}
P5021 赛道修建
题目
题目传送门
有点小难
55分思路:
细看数据,发现我们可以获得55的高分(特殊数据点):
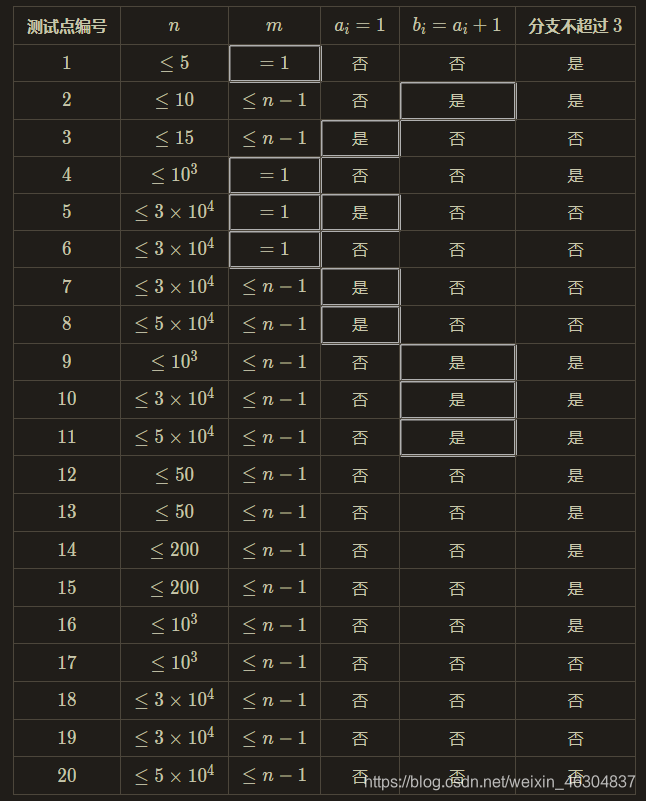
这些特殊数据的分加起来高达55 (然鹅我只拿了45)
m == 1(树的直径)
显然,就是求树的直径
做法:(简单讲)
- 以任意一点为源点,求该点到树上所有点的距离O(n)
- 找到距离最大的点,设其为b点
- 以b点为源点,求b到树上所有点的距离O(n)
- 找到距离b最远的点,距离就是树的直径
- 证明:不会
(但是好像也不用学会证明)
bi=ai+1(链)
就是一条链,原问题化为:
在一个一维数列中,把数列划分成m段,使所有段中,和最小的段的和 最大
赤裸裸的二分答案,枚举段的最小和,贪心跑一边即可
贪心;
int cnt = 0 , sum = 0;
for(int i = 1 ; i < n ; i++){
if(edlen[i] + sum < maxn){//edlen为按顺序排列的道路长度,maxn为当前二分的最小段的最大值
sum += edlen[i];
}
else{
sum = 0;
cnt++;
}
}
return cnt >= m;//按照当前最小段最大值是否可以划分出m段
ai=1(菊花图)
就是这里少了10分
就是菊花图,根据题意,每条赛道最多只能经过2条道路,排序计算即可
dfs(1);//将链式前向星的边权提取出来,存到edlen
sort(edlen + 1 , edlen + n , cmp);//大到小排序
int minn = (1 << 29);
for(int i = 1 ; i <= m ; i++){
int tmp = edlen[i] + (2 * m - i + 1 <= n - 1 ? edlen[2 * m - i + 1] : 0);
if(minn > tmp)
minn = tmp;
}
printf("%d" , minn);
55分代码
#include <iostream>
#include <cstdio>
#include <cstring>
#include <queue>
#include <algorithm>
#define nn 50010
using namespace std;
int read(){
int re = 0 , sig = 1;
char c = getchar();
while(c < '0' || c > '9'){
if(c == '-')sig = -1;
c = getchar();
}
while(c >= '0' && c <= '9'){
re = (re << 1) + (re << 3) + c - '0';
c = getchar();
}
return re * sig;
}
struct node{
int to , len , nxt;
}ed[nn * 2];
int head[nn];
void addedge(int u , int v , int len){
static int top = 1;
ed[top].len = len , ed[top].to = v;
ed[top].nxt = head[u] , head[u] = top;
top++;
ed[top].len = len , ed[top].to = u;
ed[top].nxt = head[v] , head[v] = top;
top++;
}
int n , m;
int edlen[nn];
bool vis[nn];
void work1(){
int k , maxn;
int dis[nn];
queue <int> q;
memset(dis , -1 , sizeof(dis));
dis[1] = 0 , q.push(1);
while(!q.empty()){
k = q.front() , q.pop();
for(int i = head[k] ; i ; i = ed[i].nxt){
if(dis[ed[i].to] == -1){
dis[ed[i].to] = dis[k] + ed[i].len;
q.push(ed[i].to);
}
}
}
maxn = 0;
for(int i = 1 ; i <= n ; i++)
if(dis[i] > maxn)
maxn = dis[i] , k = i;
memset(dis , -1 , sizeof(dis));
dis[k] = 0 , q.push(k);
while(!q.empty()){
k = q.front() , q.pop();
for(int i = head[k] ; i ; i = ed[i].nxt){
if(dis[ed[i].to] == -1){
dis[ed[i].to] = dis[k] + ed[i].len;
q.push(ed[i].to);
}
}
}
maxn = 0;
for(int i = 1 ; i <= n ; i++)
if(dis[i] > maxn)
maxn = dis[i];
printf("%d" , maxn);
}
void dfs(int x){
static int siz = 1;
vis[x] = true;
for(int i = head[x] ; i ; i = ed[i].nxt){
if(!vis[ed[i].to]){
dfs(ed[i].to);
edlen[siz] = ed[i].len;
siz++;
}
}
}
bool cmp(int a , int b){return a > b;}
void work2(){
dfs(1);
sort(edlen + 1 , edlen + n , cmp);
int minn = (1 << 29);
for(int i = 1 ; i <= m ; i++){
int tmp = edlen[i] + (2 * m - i + 1 <= n - 1 ? edlen[2 * m - i + 1] : 0);
if(minn > tmp)
minn = tmp;
}
printf("%d" , minn);
}
bool check(int maxn){
int cnt = 0 , sum = 0;
for(int i = 1 ; i < n ; i++){
if(edlen[i] + sum < maxn){
sum += edlen[i];
}
else{
sum = 0;
cnt++;
}
}
return cnt >= m;
}
void work3(){
dfs(1);
int sum = 0;
for(int i = 1 ; i < n ; i++)
sum += edlen[i];
int l = 1 , r = sum;
while(l < r){
int mid = (l + r) / 2;
if((l + r) & 1)
mid++;
if(check(mid)) l = mid;
else r = mid - 1;
}
printf("%d" , l);
}
void work4(){
dfs(1);
int sum = 0;
for(int i = 1 ; i < n ; i++)
sum += edlen[i];
printf("%d" , sum);
}
int main(){
bool ty1 , ty2;
ty1 = ty2 = true;
n = read(); m = read();
for(int i = 1 ; i < n ; i++){
int u , v , len;
u = read() , v = read() , len = read();
addedge(u , v , len);
if(u != 1) ty1 = false;
if(v != u + 1) ty2 = false;
}
if(m == 1){
work1();
return 0;
}
if(m == n - 1){
work4();
return 0;
}
if(ty1){
work2();
return 0;
}
if(ty2){
work3();
return 0;
}
return 0;
}
100分思路
建议不要看本蒟蒻的:搞了半天,WA变成了TLE,然后卡常,会用的技巧都用了,结果第6个和第18个还是TLE,无可奈何之下,第6个点求了树的直径,第18个点O2也过了话说O2真好用啊


讲正事儿
首先是二分,同链的情况,设所有赛车路径中长度最小值为maxn
对于每一个结点x,记以x为端点,x的子树中的某个结点为另一个端点,组成的所有的路径中长度最大且小于(不能等)maxn的值为f[x] (如果大于等于maxn的话直接cnt++就好了,不用记录,原因要看f[]的作用,待会就知道了)
有了f,问题和菊花图有点像了。
- 首先,令si为x的某个子结点,则任意f[si]<maxn,即不能单独成为一条合法赛道(原因见f的定义)(我们称长度大于等于maxn的赛道合法);
- 但是,若将那些道路延长到x结点,就有可能成为合法赛道,并将这些赛道除去,我们将剩下的不合法赛道长度记录在tmp数组里面;
- 我们考虑以x为中转点,将剩下的赛道两两合并,使合并后合法赛道数量最大化
- 满足当前合法赛道数量最大的前提下,还要满足在x上方的点(父节点)的合法赛道数量最大化,因此,我们将没有合并的赛道中最长的一个记录在f[x]中,供x的父节点使用
- 由于使合法赛道数量最大的方案不止一种,我们又双叒叕考虑二分:将tmp取出,二分tmp的下标mid,若舍去tmp[mid]后合法赛道数量仍然可以到达最大值,就将mid前移(tmp[mid]增大),否则mid后移
- 关于如何求最大合法赛道数量的问题:贪心:(tmp已经从大到小排序的前提下)j=siz(siz为tmp的数组大小),i从前向后枚举,j向前找到第一个满足tmp[i]+tmp[j]>=maxn的树,cnt++,j--,当i>=j时结束
- 请仔细思考贪心的正确性
100分代码
#include <iostream>
#include <cstdio>
#include <cstring>
#include <queue>
#include <algorithm>
#include <vector>
#define rr register
#define nn 50010
using namespace std;
int read(){
int re = 0 , sig = 1;
char c = getchar();
while(c < '0' || c > '9'){
if(c == '-')sig = -1;
c = getchar();
}
while(c >= '0' && c <= '9'){
re = (re << 1) + (re << 3) + c - '0';
c = getchar();
}
return re * sig;
}
struct node{
int to , len , nxt;
}ed[nn * 2];
int head[nn];
void addedge(int u , int v , int len){
static int top = 1;
ed[top].len = len , ed[top].to = v;
ed[top].nxt = head[u] , head[u] = top;
top++;
ed[top].len = len , ed[top].to = u;
ed[top].nxt = head[v] , head[v] = top;
top++;
}
int n , m;
int lensum = 0;
bool vis[nn];
int f[nn];
int cnt;
void work1(){//专门解决为第6个点TLE而copy55分的
int k , maxn;
int dis[nn];
queue <int> q;
memset(dis , -1 , sizeof(dis));
dis[1] = 0 , q.push(1);
while(!q.empty()){
k = q.front() , q.pop();
for(int i = head[k] ; i ; i = ed[i].nxt){
if(dis[ed[i].to] == -1){
dis[ed[i].to] = dis[k] + ed[i].len;
q.push(ed[i].to);
}
}
}
maxn = 0;
for(int i = 1 ; i <= n ; i++)
if(dis[i] > maxn)
maxn = dis[i] , k = i;
memset(dis , -1 , sizeof(dis));
dis[k] = 0 , q.push(k);
while(!q.empty()){
k = q.front() , q.pop();
for(int i = head[k] ; i ; i = ed[i].nxt){
if(dis[ed[i].to] == -1){
dis[ed[i].to] = dis[k] + ed[i].len;
q.push(ed[i].to);
}
}
}
maxn = 0;
for(int i = 1 ; i <= n ; i++)
if(dis[i] > maxn)
maxn = dis[i];
printf("%d" , maxn);
}
int tmp[nn] , siz = 0;//将tmp存为全局变量以节省空间
bool cmp(int a , int b){return a > b;}
void dfs(rr int x , rr int maxn){
vis[x] = true;
for(rr int i = head[x] ; i ; i = ed[i].nxt)//先遍历x的每一个子结点以防止tmp在递归时冲突
if(!vis[ed[i].to]){
dfs(ed[i].to , maxn);
}
siz = 0;
for(rr int i = head[x] ; i ; i = ed[i].nxt)
if(!vis[ed[i].to]){
if(f[ed[i].to] + ed[i].len >= maxn) cnt++;//若此赛道延长到x点后长度到达maxn,直接cnt++
else tmp[++siz] = f[ed[i].to] + ed[i].len;//否则记录到tmp
}
sort(tmp + 1 , tmp + siz + 1 , cmp);//大到小排序
int nowcnt = 0;
for(rr int i = 1 , j = siz ; i < j ; ++i){//求以x为根的树中最大合法赛道数量
while(tmp[i] + tmp[j] < maxn)
--j;
if(i >= j)
break;
++nowcnt;
--j;
}
f[x] = 0;
//二分(不知道能不能像主函数里那个二分那样写,反正当时出错改了就没有再改回去)
rr int l = 1 , r = siz;
rr int mid;
rr int res = 0;
while(l <= r){
mid = (l + r) / 2;
rr int cntt = 0;
rr int i = 1 , j = siz;
for( ; i < j ; i++){
if(i == mid)continue;//舍去mid结点求最大合法赛道数量
while(tmp[i] + tmp[j] < maxn || j == mid)
--j;
if(i >= j)
break;
++cntt;
--j;
}
if(nowcnt == cntt) r = mid - 1 , res = mid;
else l = mid + 1;
}
cnt += nowcnt;
f[x] = tmp[res];
vis[x] = false;
}
bool check(int maxn){
memset(f , 0 , sizeof(f));//记得初始化
memset(vis , 0 , sizeof(vis));
cnt = 0;
dfs(1 , maxn);
return cnt >= m;
}
int main(){
bool ty1 , ty2;
ty1 = ty2 = true;
n = read(); m = read();
for(int i = 1 ; i < n ; i++){
int u , v , len;
u = read() , v = read() , len = read();
lensum += len;
addedge(u , v , len);
}
if(m == 1){
work1();
return 0;
}
rr int l = 1 , r = lensum;
r/=m;
while(l < r){//大二分
int mid = (l + r) / 2;
if((l + r) & 1) mid++;
if(check(mid)) l = mid;
else r = mid - 1;
}
printf("%d" , l);
return 0;
}