定点数加减运算
补码加法:
负数用补码表示后,可以和正数一样去处理
当需要减去一个数x的时候,可以用加上x对应的负数的补码【-x】补来代替
【x】补+【y】补=【x+y】补
补码减法
【x-y】补=【x】补+【-y】补(mod 2)
【x-y】补=【x】补+【-y】补 (mod 2的n+1次方)
补码基本规则:
- 运算的各个操作数均用补码表示,运算结果仍是补码
- 符号位和数值位一样参加运算
- 如果求和,则将两补码直接相加,得到两数之和的补码,若求差,则将减数变补(【y】补变【-y】补),然后和被减数相加,得到两数之差的补码
- 如果超过则模丢掉
溢出:
两个正数相加结果变为负数 溢出
两个负数相加结果变为正数 溢出
双符号位也叫变形补码(00表示正 11表示负) 符号位参加运算如果结果出现 01 或10 则发生溢出
单符号位:最高数值位产生进位符号位五金位产生上溢 最高有效位无进位符号位有进位产生下一,也就是当都有进位或都没有进位时不产生溢出,用异或们表示。
定点乘法:
原码一位乘法:数值位相乘 符号位单独处理
乘积的位数扩大一倍(两个4位相乘变成8位)
改进乘法:

定点除法
原码除法运算原理
两个原码表示的数相除,商的符号由两数的符号按位相加求得,商的部分由两数的数值部分相除求得。
被除数x原码为【x】原=XfXn-1.....X1X0
除数y原码【y】原=YfYn-1....y1y0
则有商q=x/y其原码为
【q】原=(Xf异或Yf)+(0.Xn-1...X1X0/0.Yn-1...Y1Y0)

恢复余数法:
机器必须现做减法,若余数为正才知道够减,若余数为负,才知道不够减。不够减是必须回复原来的余数,以便在继续往下,这种称为恢复余数法。
不恢复余数法:
但由于要恢复余数,使除法进行过程的步数不固定,因此控制比较复杂
实际中常用不恢复余数法,又称加减交替法,重点是运算过程中如出现不够减则不必恢复余数,根据余数符号,可以继续往下运算,因此步数固定,控制简单。


真题
1、假定在一个8位字长的计算机中进行如下类C程序
1 unsigned int x=134; 2 unsigned int y=246; 3 int m=x;int n=y; 4 unsigned int z1=x-y; 5 unsigned int z2=x+y; 6 int k1=m-n; 7 int k2=m+n;
若编译的时候将8个8位寄存器R1~R8分别分配给x y m n z1 z2 k1 k2请回答下列问题(带符号整数用补码表示)
1)执行上述程序段后,寄存器R1 R5 R6和分别是什么,十六进制表示
2)执行后,变量m和k1的值分别是多少(十进制)
3)上述程序段设计带符号的整数加减 ,无符号整数的加减运算 四种运算能否利用同一个加法器及辅助电路实现?
4)计算机内部如果判断带符号的整数加减运算的结果是否溢出,上述程序段中,那些带符号整数运算语句的执行结果会溢出
| R1 | R2 | R3 | R4 | R5 | R6 | R7 | R8 |
| X | Y | m | n | z1 | z2 | k1 | k2 |
| 无符号 | 无符号 |
答:1)x=134=1000 0110=86H Y=246=1111 0110=F6H
R5=x-y=134-246=-112->1111 0000->1 001 0000(补)=90H
R6:z2=134+246=380=1 0111 1100=7CH(高位丢弃了)
2)m补=x=1000 0110->m=1111 1010 =-122
n补=y=1111 0110->n=1000 1010 =-10
k1=m-n=-122-(-10)=-112
3)能 无符号数有符号数都是二进制代码,有符号数的符号位代码化了,和数值位一样参加运算,减一个数等于加上整数对应的负数的补码
4)双符号位 单符号位等
2、

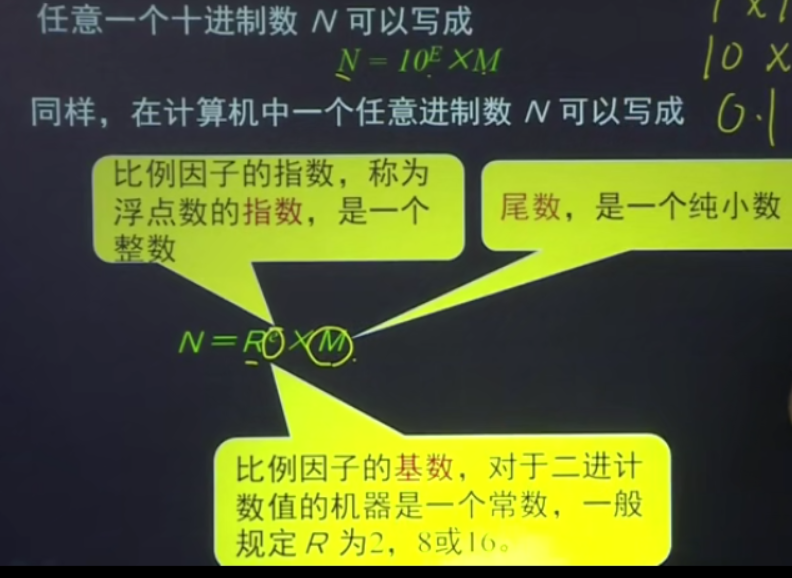
浮点数的表示方法
| 31 | 23-30 | 0-22 | |
| 32位 | S符号位 | E移码表示 127 | M尾数 |
| 63 | 52-62 | 0-51 | |
| 64位 | S符号位 | E移码表示 1023 | M尾数 |
32位浮点数中,将浮点数的指数真值e变为阶码,应将指数e加上一个固定的偏移量127(01111111) E=e+127 .因为阶码是用移码表的
规格化:当尾数的值不为0时,尾数域的最高位应为1,否则修改阶码同事左右移小数点的办法,使其变成这一表示方式,这称为浮点数的规格化表示。因为尾数的最高位总为1,所以这一位不需要存储而是默认存在、
当阶码E全0(00000000)且尾数M也全为0时,表示的真值x为0,结合符号位s为0或1,有正零和负零之分
当阶码全是1(11111111)且尾数M为全0,表示的浮点数位无穷大,结合符号位S为0或1,也有正无穷大和负无穷大之分、
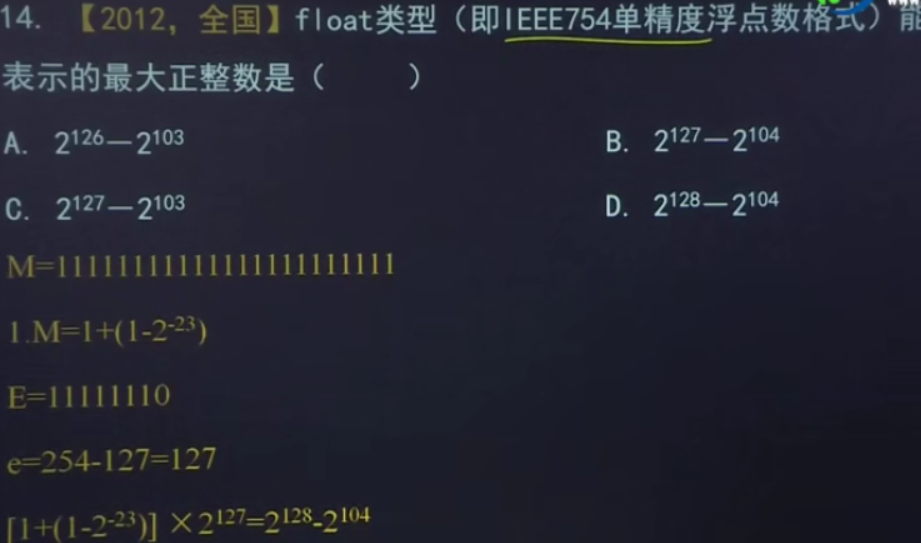
32位浮点数表示除去全0和全1阶码范围为00000001 到1111 1110 也就是1到254
规格化浮点数指数e则为-126(1-127)到127(154-127)




浮点数的加减运算

因为右移丢失的误差小,所以采用尾数右移,对阶的原则是小阶向大阶对齐,尾数右移1位阶码+1.


浮点数的溢出:
上溢发生中断 下溢不发生中断
例题:




D
