简单数论总结1——gcd与lcm

并不重要的前言

　　最近学习了一些数论知识，但是自己都不懂自己到底学了些什么qwq，在这里把知识一并总结起来。

也不是很难的gcd和lcm

 　　显而易见的结论：

　　为什么呢？

　　根据唯一分解定理：

　　　　　　　　a和b都可被分解为素因子的乘积，形如：

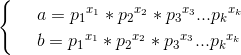
　　则显而易见的有一下结论：

　

　

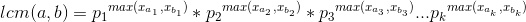
　　相乘，得：

　

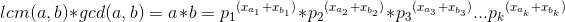
　　得证

 

几种求gcd的算法

1. 1. 　　欧几里得算法（辗转相除法）
   2.      辗转相减法（优化：stein_gcd）　　

　　　　　　

　　　　　欧几里得算法

　基于事实:

　　

　实现：

int gcd(int a, int b){
  return (b == 0) ? a : gcd( b , a % b) ;          
}

　　简短而容易实现和记忆，非常优美

　　但是可能会被斐波那契数列卡住，证明或者原因鸽了回头再写

　　　　　　stein_gcd算法

　　stein_gcd本质上是对更相减损术的优化，下面进行简单的介绍：

1. 　　若a,b都是偶数，则计算gcd(a/2,b/2)*2;  ————>因为都含有2的因数，所以同时除以2后gcd(a,b)变为原来的1/2，再乘回去
2.        若a是偶数，b是奇数，则计算gcd(a/2,b);  ————>因为只有一个数含有2作为因数，所以除以2后gcd(a,b)不变
3.        若a是奇数，b是偶数，则计算gcd(a,b/2);  ————>同2.
4.        若a是奇数，b是奇数，则计算gcd(abs(x-y),min(x,y)); ————>通过相减，使其变成偶数，原理参见更相减损术其实是我懒得写

 　　实现：

int stein_gcd(int x,int y){
  if(x==0)
    return y;
  if(y==0)
    return x;
  if(x%2==0&&y%2==0)
    return stein_gcd(x>>1,x>>1)*2;
  else if(x%2 ==0)
    return stein_gcd(x>>1,y);
  else if(y%2==0)
    return stein_gcd(x,y>>1);
  else
    return stein_gcd(abs(x-y),min(x,y));                                 
}

　　讲到这里，大概本期就结束了，至于没涉及到的，就是鸽了下一期的事情了

　　至于下一次什么时候填坑，已经在做了逃