移动平均线
简单移动平均线
关键函数: np.convolve()
简单移动平均线是数列与等权重的指示函数的卷积
import sys import numpy as np import matplotlib.pyplot as plt N = 5 weights = np.ones(N) / N print("Weights",weights) #生成等权重的指示函数 # [ 0.2 0.2 0.2 0.2 0.2] c = np.loadtxt('my.csv',delimiter=',', usecols=(6,), unpack=True) # 读取my.csv的第6列,是一个一维数组 print(c) sma = np.convolve(weights,c)[N-1:-N+1] # 取第5个数据到-5个数据 # convolve的第一个数据为第一天的原值*0.2 # 第二个数据是第二天的原值*0.2加第一天的原值0.2 # 第三个数据是(第三天的原值+第二天的原值+第一天的原值)*0.2 # ... # 第5天的数据就是前五天的数据的平均值 # 然后之后的每个数据都是这一天到五天后,这五天数据的平均值 # 最后舍掉最后的四天 print(sma) t = np.arange(N-1,len(c)) # 生成表示时间的数组,作为横坐标 plt.plot(t,c[N-1:],lw=1.0) # t为横坐标,c[N-1:]作为纵坐标 plt.plot(t,sma,lw=2.0) # plt.plot第一个参数为x轴,第二个参数为y轴,lw为linewidth线宽 plt.show() # 显示图表
np.convolve()函数使用详情可参考另一博客:
https://www.cnblogs.com/draven123/p/11370867.html
指数移动平均线
关键函数: np.exp() np.linspace()
指数移动平均线使用的权重是指数衰减的.
对历史上的数据点赋予的权重以指数速度减小,但永远不会到达0
import numpy as np import matplotlib.pyplot as plt x = np.arange(5) # np.exp()函数 print(np.exp(x)) # 生成e关于x的指数 # [ 1. 2.71828183 7.3890561 20.08553692 54.59815003] # np.linspace()函数 print(np.linspace(-1, 0, 5)) # 注意:不是linespace # [-1. -0.75 -0.5 -0.25 0. ] # 生成从-1到0的数量为5的等差数列 # 生成权重值 N = 5 weights = np.exp(np.linspace(-1, 0, N)) # [ 0.36787944 0.47236655 0.60653066 0.77880078 1. ] # 对权重值做归一化处理 weights /= weights.sum() print(weights) # [ 0.11405072 0.14644403 0.18803785 0.24144538 0.31002201] c = np.loadtxt('my.csv', delimiter=',', usecols=(6,), unpack=True) ema = np.convolve(weights, c)[N-1:-N+1] # 生成的数组长度为len(c) - (N -1) # 生成的数不是像简单移动平均线那样取当天加上前四天共五天的均值 # 而是按照指数,第一天的比重最低,之后慢慢增加,当天的权重最高 t = np.arange(N-1, len(c)) # 生成x轴
布林带
关键函数: np.fill()
布林带用来刻画价格波动的区间. 由三条轨道线组成一个带状通道
上轨: 比简单移动平均线高两倍标准差的举例
中轨: 简单移动平均线
下轨: 比简单移动平均线低两倍标准差
# 这里的标准差是简单移动平均线所用的数据, 计算出来的标准差
import numpy as np import matplotlib.pyplot as plt ''' # fill函数的简单介绍 >>> a = np.array([1, 2]) >>> a.fill(0) >>> a array([0, 0]) >>> a = np.empty(2) >>> a.fill(1) >>> a array([ 1., 1.]) ''' N = 5 weights = np.ones(N) / N # 读取文本的第6列 c = np.loadtxt('my.csv', delimiter=',', usecols=(6,), unpack=True) # 生成简单移动平均线的y值,数组长度为len(c) - (N - 1) sma = np.convolve(weights, c)[N-1:-N+1] # sma中的每个值都是c中5个数值的平均值 # sma第一个元素是c中前5个数值的均值,其余类推 deviation = [] C = len(c) # dev代表当前数和其后的四个数组成的数组 # 最后四个数后没有足够的数组成数组,就都用c的最后五个数代替 for i in range(N - 1, C): if i + N < C: dev = c[i: i + N] # 长度为N - 1 else: dev = c[-N:] averages = np.zeros(N) # 生成N个元素的0矩阵 averages.fill(sma[i - N - 1]) # 将average全部元素标量成定值 # fill函数将数组元素的值全部设置为一个指定的标量值 dev = dev - averages dev = dev ** 2 dev = np.sqrt(np.mean(dev)) # 如上3步是计算c中每5个数的标准差 deviation.append(dev) deviation = 2 * np.array(deviation) # 计算2倍标准差 upperBB = sma + deviation # 得出上轨 lowerBB = sma - deviation # 得出下轨 # 生成作为x轴的时间序列 t = np.arange(N -1, C) plt.plot(t, c[N-1:C], lw=1.0) plt.plot(t, sma, lw=2.0) plt.plot(t, upperBB, lw=3.0) plt.plot(t, lowerBB, lw=4.0) plt.show()
线性模型
Numpy的linalg包是专门做线性代数计算的
import numpy as np import matplotlib.pyplot as plt N = 5 weights = np.ones(N) / N c = np.loadtxt('my.csv', delimiter=',', usecols=(5,), unpack=True) sma = np.convolve(weights, c)[N-1: -N+1] b = c[-N:] b = b[::-1] # 反转原来的b print(b) # [ 351.99 346.67 352.47 355.76 355.36] # 初始化一个N*N的二维数组A, 全部元素为0 A = np.zeros((N,N),float) print(A) ''' [[ 0. 0. 0. 0. 0.] [ 0. 0. 0. 0. 0.] [ 0. 0. 0. 0. 0.] [ 0. 0. 0. 0. 0.] [ 0. 0. 0. 0. 0.]] ''' # 用b向量中的N个股价值填充数组A for i in range(N): A[i,] = c[- N - 1 - i: -1 - i] print(A) ''' [[ 360. 355.36 355.76 352.47 346.67] [ 359.56 360. 355.36 355.76 352.47] [ 352.12 359.56 360. 355.36 355.76] [ 349.31 352.12 359.56 360. 355.36] [ 353.21 349.31 352.12 359.56 360. ]] ''' # 使用linalg包中的lstsq函数确定线性模型中的系数 (x, residuals, rank, s) = np.linalg.lstsq(A ,b) print(x, residuals, rank, s) ''' x: [ 0.78111069 -1.44411737 1.63563225 -0.89905126 0.92009049] residuals: [] rank: 5 s: [ 1.77736601e+03 1.49622969e+01 8.75528492e+00 5.15099261e+00 1.75199608e+00] ''' # x是系数向量 # residuals是一个残差数组 # rank是A的秩 # s是A的奇异值 # 奇异值: 设A为m*n阶矩阵,q=min(m,n),A*A的q个非负特征值的算术平方根叫作A的奇异值 # 使用numpy中的dot函数计算点乘 # 点乘就是向量的内积 print(np.dot(b, x)) # 357.939161015 print(np.dot(x, b)) # 357.939161015
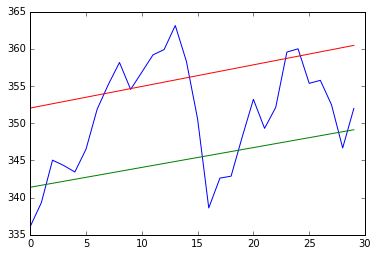
趋势线
趋势线就是数据随时间序列变化的趋势
# 确定枢轴点的位置 # 本例中使用最高价,最低价和收盘价的算数平均值 h, l, c = np.loadtxt('my.csv', delimiter=',', usecols=(3,4,5), unpack=True) # h是最高价, l是最低价, c是收盘价 pivots = (h + l + c) / 3 print(pivots) ''' [ 338.01 337.88666667 343.88666667 344.37333333 342.07666667 345.57 350.92333333 354.29 357.34333333 354.18 356.06333333 358.45666667 359.14 362.84333333 358.36333333 353.19333333 340.57666667 341.95666667 342.13333333 347.13 353.12666667 350.90333333 351.62333333 358.42333333 359.34666667 356.11333333 355.13666667 352.61 347.11333333 349.77 ] ''' # 从枢轴点推导除阻力位和支撑位 # 阻力位: 股价上升时遇到阻力,转跌前的最高价格 # 支撑位: 股价下跌时遇到支撑,反弹前的最低价格 # 定义一个函数y=at+b来拟合数据 # 将直线方程写成y=Ax的形式 def fit_line(t, y): A = np.vstack([t, np.ones_like(t)]).T return np.linalg.lstsq(A, y)[0] # 假设支撑位在枢轴点下方当日股价区间的位置 # 阻力位在枢轴点上方当日股价区间的位置 t = np.arange(len(c)) sa, sb = fit_line(t, pivots - (h - l)) ra, rb = fit_line(t, pivots + (h - l)) support = sa * t + sb resistance = ra * t + rb condition = (c > support) & (c < resistance) print(condition) ''' [False False True True True True True False False True False False False False False True False False False True True True True False False True True True False True] ''' between_bands = np.where(condition) ''' (array([ 2, 3, 4, 5, 6, 9, 15, 19, 20, 21, 22, 25, 26, 27, 29]),) ''' print(support[between_bands]) ''' [ 341.92421382 342.19081893 342.45742405 342.72402917 342.99063429 343.79044964 345.39008034 346.4565008 346.72310592 346.98971104 347.25631615 348.0561315 348.32273662 348.58934174 349.12255197] ''' print(c[between_bands]) ''' [ 345.03 344.32 343.44 346.5 351.88 354.54 350.56 348.16 353.21 349.31 352.12 355.36 355.76 352.47 351.99] ''' print(resistance[between_bands]) ''' [ 352.61688271 352.90732765 353.19777259 353.48821753 353.77866246 354.64999728 356.39266691 357.55444667 357.84489161 358.13533655 358.42578149 359.2971163 359.58756124 359.87800618 360.45889606] ''' between_bands = len(np.ravel(between_bands)) # 15 plt.plot(t, c) plt.plot(t, support) plt.plot(t, resistance) plt.show()