Eddy's mistakes[HDU1161]
Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 65536/32768 K (Java/Others)
Total Submission(s): 6014 Accepted Submission(s): 3405
Problem Description
Eddy usually writes articles ,but he likes mixing the English letter uses, for example "computer science" is written frequently "coMpUtEr scIeNce" by him, this mistakes lets Eddy's English teacher be extremely discontentment.Now please you to write a procedure to be able in the Bob article English letter to turn completely the small letter.
Input
The input contains several test cases.each line consists a test case,Expressed Eddy writes in an article , by letter, blank space,numeral as well as each kind of punctuation
composition, the writing length does not surpass 1000 characters.
Output
For each test case, you should output an only line, after namely the result of transforms the lowercase letter.
Sample Input
weLcOmE tO HDOj Acm 2005!
Sample Output
welcome to hdoj acm 2005!
Author
eddy
Recommend
JGShining

#include<stdio.h>
#include<string.h>
int main()
{
char str[2000];
int n,i;
while (gets(str))
{
int n=strlen(str);
for (i=0;i<n;i++)
if ('A'<=str[i] && str[i]<='Z')
str[i]=str[i]-'A'+'a';
puts(str);
}
return 0;
}
Eddy's picture[HDU1162]
Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 65536/32768 K (Java/Others)
Total Submission(s): 5245 Accepted Submission(s): 2601
Problem Description
Eddy begins to like painting pictures recently ,he is sure of himself to become a painter.Every day Eddy draws pictures in his small room, and he usually puts out his newest pictures to let his friends appreciate. but the result it can be imagined, the friends are not interested in his picture.Eddy feels very puzzled,in order to change all friends 's view to his technical of painting pictures ,so Eddy creates a problem for the his friends of you.
Problem descriptions as follows: Given you some coordinates pionts on a drawing paper, every point links with the ink with the straight line, causes all points finally to link in the same place. How many distants does your duty discover the shortest length which the ink draws?
Input
The first line contains 0 < n <= 100, the number of point. For each point, a line follows; each following line contains two real numbers indicating the (x,y) coordinates of the point.
Input contains multiple test cases. Process to the end of file.
Output
Your program prints a single real number to two decimal places: the minimum total length of ink lines that can connect all the points.
Sample Input
3
1.0 1.0
2.0 2.0
2.0 4.0
Sample Output
3.41
Author
eddy
Recommend
JGShining

#include<math.h>
#include<stdio.h>
#include<string.h>
double x[125],y[125],dis[125][125],d[125];
int N;
bool s[125];
double prim()
{
int i,j;
for (i=1;i<=N;i++)
for (j=1;j<=N;j++)
dis[i][j]=sqrt((x[i]-x[j])*(x[i]-x[j])+(y[i]-y[j])*(y[i]-y[j]));
memset(s,0,sizeof(s));
s[1]=true;
d[1]=0;
double ans=0;
for (i=2;i<=N;i++) d[i]=dis[i][1];
for (i=1;i<N;i++)
{
double Min=10000000000;
int v;
for (j=1;j<=N;j++)
if (!s[j] && d[j]<Min)
{
Min=d[j];
v=j;
}
s[v]=true;
ans+=d[v];
for (j=1;j<=N;j++)
if (!s[j] && d[j]>dis[j][v]) d[j]=dis[j][v];
}
return ans;
}
int main()
{
int i;
while (scanf("%d",&N)!=EOF)
{
for (i=1;i<=N;i++) scanf("%lf%lf",&x[i],&y[i]);
printf("%.2lf
",prim());
}
return 0;
}
Eddy's digital Roots[HDU1163]
Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 65536/32768 K (Java/Others)
Total Submission(s): 3424 Accepted Submission(s): 1934
Problem Description
The digital root of a positive integer is found by summing the digits of the integer. If the resulting value is a single digit then that digit is the digital root. If the resulting value contains two or more digits, those digits are summed and the process is repeated. This is continued as long as necessary to obtain a single digit.
For example, consider the positive integer 24. Adding the 2 and the 4 yields a value of 6. Since 6 is a single digit, 6 is the digital root of 24. Now consider the positive integer 39. Adding the 3 and the 9 yields 12. Since 12 is not a single digit, the process must be repeated. Adding the 1 and the 2 yeilds 3, a single digit and also the digital root of 39.
The Eddy's easy problem is that : give you the n,want you to find the n^n's digital Roots.
Input
The input file will contain a list of positive integers n, one per line. The end of the input will be indicated by an integer value of zero. Notice:For each integer in the input n(n<10000).
Output
Output n^n's digital root on a separate line of the output.
Sample Input
2
4
0
Sample Output
4
4
Author
eddy
Recommend
JGShining
For digital root there is a characteristic saying it will never change when plused or multiplied by 9.
From this we can reason that R(A+B)=R(R(A)+R(B))and R(A*B)=R(R(A)*R(B)).It can be proved easily through see A as 9a+x,while B as 9b+y.

#include<stdio.h>
int R(int x)
{
int tmp=x,ans=0;
if (x<10) return x;
while (tmp)
{
ans+=tmp%10;
tmp/=10;
}
return R(ans);
}
int pow(int x,int n)
{
if (n==0) return 1;
if (n==1) return R(x);
int tmp=pow(x,n/2);
if (n&1) return R(tmp*tmp*x);
else return R(tmp*tmp);
}
int main()
{
int n;
while (scanf("%d",&n)!=EOF)
{
if (n<=0) return 0;
printf("%d
",pow(R(n),n));
}
return 0;
}
Eddy's research I[HDU1164]
Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 65536/32768 K (Java/Others)
Total Submission(s): 4967 Accepted Submission(s): 2973
Problem Description
Eddy's interest is very extensive, recently he is interested in prime number. Eddy discover the all number owned can be divided into the multiply of prime number, but he can't write program, so Eddy has to ask intelligent you to help him, he asks you to write a program which can do the number to divided into the multiply of prime number factor .
Input
The input will contain a number 1 < x<= 65535 per line representing the number of elements of the set.
Output
You have to print a line in the output for each entry with the answer to the previous question.
Sample Input
11
9412
Sample Output
11
2*2*13*181
Author
eddy
Recommend
JGShining

#include<stdio.h>
#include<string.h>
int p[65536];
bool f[70000];
int n,T;
void getprime()
{
int i,j;
memset(f,true,sizeof(f));
for (i=2;i<65536;i++)
if (f[i])
for (j=i+i;j<65536;j+=i) f[j]=false;
for (i=2;i<65536;i++)
if (f[i])
{
T++;
p[T]=i;
}
}
int main()
{
getprime();
while (scanf("%d",&n)!=EOF)
{
int i;
for (i=1;i<=T;i++)
if (n%p[i]==0)
{
while (n%p[i]==0)
{
printf("%d",p[i]);
n/=p[i];
if (n>1) printf("*");
}
}
printf("
");
}
return 0;
}
Eddy's research II[HDU1165]
Time Limit: 4000/2000 MS (Java/Others) Memory Limit: 65536/32768 K (Java/Others)
Total Submission(s): 2502 Accepted Submission(s): 911
Problem Description
As is known, Ackermann function plays an important role in the sphere of theoretical computer science. However, in the other hand, the dramatic fast increasing pace of the function caused the value of Ackermann function hard to calcuate.
Ackermann function can be defined recursively as follows:
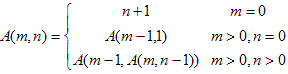
Now Eddy Gives you two numbers: m and n, your task is to compute the value of A(m,n) .This is so easy problem,If you slove this problem,you will receive a prize(Eddy will invite you to hdu restaurant to have supper).
Input
Each line of the input will have two integers, namely m, n, where 0 < m < =3.
Note that when m<3, n can be any integer less than 1000000, while m=3, the value of n is restricted within 24.
Input is terminated by end of file.
Output
For each value of m,n, print out the value of A(m,n).
Sample Input
1 3
2 4
Sample Output
5
11
Author
eddy
Recommend
JGShining
The crazy increasing of Ackermann function is from its uncountable recursive call.So if you want to calculate it just as how it comes to you,I sure your program will stackoverflow.
In this question ,m is limited within 3,which gives us a chance to get the formula of Ackermann function when m equals between 0 and 3.
/*A(1,0)=A(0,1)=2
A(1,x)=A(0,A(1,x-1))=A(1,x-1)+1
#A(1,x)=x+2
A(2,0)=A(1,1)=3
A(2,x)=A(1,A(2,x-1))=A(2,x-1)+2
#A(2,x)=2x+3
A(3,0)=A(2,1)=5
#A(3,x)=A(2,A(3,x-1))=2A(3,x-1)+3*/

#include<stdio.h>
int Ackermann(int m,int n)
{
if (m==0) return n+1;
if (m==1) return n+2;
if (m==2) return 2*n+3;
if (m==3 && n==0) return 5;
return 2*Ackermann(m,n-1)+3;
}
int main()
{
int m,n;
while (scanf("%d%d",&m,&n)!=EOF) printf("%d
",Ackermann(m,n));
return 0;
}
Eddy's 洗牌问题[HDU1210]
Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 65536/32768 K (Java/Others)
Total Submission(s): 2636 Accepted Submission(s): 1740
Problem Description
Eddy是个ACMer,他不仅喜欢做ACM题,而且对于纸牌也有一定的研究,他在无聊时研究发现,如果他有2N张牌,编号为1,2,3..n,n+1,..2n。这也是最初的牌的顺序。通过一次洗牌可以把牌的序列变为n+1,1,n+2,2,n+3,3,n+4,4..2n,n。那么可以证明,对于任意自然数N,都可以在经过M次洗牌后第一次重新得到初始的顺序。编程对于小于100000的自然数N,求出M的值。
Input
每行一个整数N
Output
输出与之对应的M
Sample Input
20
1
Sample Output
20
2
Author
Eddy
Source
杭电ACM省赛集训队选拔赛之热身赛
Recommend
Eddy

#include<stdio.h>
int main()
{
int N;
while (scanf("%d",&N)!=EOF)
{
int R=2,T=1;
while (R!=1)
{
if (R<=N) R*=2;
else R=(R*2-1)%(2*N);
T++;
}
printf("%d
",T);
}
return 0;
}
Eddy's AC难题[HDU2200]
Time Limit: 3000/1000 MS (Java/Others) Memory Limit: 32768/32768 K (Java/Others)
Total Submission(s): 2940 Accepted Submission(s): 1380
Problem Description
Eddy是个ACMer,他不仅喜欢做ACM题,而且对于Ranklist中每个人的ac数量也有一定的研究,他在无聊时经常在纸上把Ranklist上每个人的ac题目的数量摘录下来,然后从中选择一部分人(或者全部)按照ac的数量分成两组进行比较,他想使第一组中的最小ac数大于第二组中的最大ac数,但是这样的情况会有很多,聪明的你知道这样的情况有多少种吗?
特别说明:为了问题的简化,我们这里假设摘录下的人数为n人,而且每个人ac的数量不会相等,最后结果在64位整数范围内.
Input
输入包含多组数据,每组包含一个整数n,表示从Ranklist上摘录的总人数。
Output
对于每个实例,输出符合要求的总的方案数,每个输出占一行。
Sample Input
2
4
Sample Output
1
17
Author
Eddy
Recommend
lcy

#include<stdio.h>
__int64 s[64],d[64];
void init()
{
int i;
s[0]=1;
for (i=1;i<64;i++) s[i]=s[i-1]<<1;
d[0]=0;d[1]=0;d[2]=1;
for (i=3;i<64;i++) d[i]=2*d[i-1]+s[i-1]-1;
}
int main()
{
init();
int N;
while (scanf("%d",&N)!=EOF) printf("%I64d
",d[N]);
return 0;
}
Eddy's爱好[HDU2204]
Time Limit: 3000/1000 MS (Java/Others) Memory Limit: 32768/32768 K (Java/Others)
Total Submission(s): 1090 Accepted Submission(s): 473
Problem Description
Ignatius 喜欢收集蝴蝶标本和邮票,但是Eddy的爱好很特别,他对数字比较感兴趣,他曾经一度沉迷于素数,而现在他对于一些新的特殊数比较有兴趣。
这些特殊数是这样的:这些数都能表示成M^K,M和K是正整数且K>1。
正当他再度沉迷的时候,他发现不知道什么时候才能知道这样的数字的数量,因此他又求助于你这位聪明的程序员,请你帮他用程序解决这个问题。
为了简化,问题是这样的:给你一个正整数N,确定在1到N之间有多少个可以表示成M^K(K>1)的数。
Input
本题有多组测试数据,每组包含一个整数N,1<=N<=1000000000000000000(10^18).
Output
对于每组输入,请输出在在1到N之间形式如M^K的数的总数。
每组输出占一行。
Sample Input
10
36
1000000000000000000
Sample Output
4
9
1001003332
Author
Eddy
Recommend
lcy

#include<math.h>
#include<stdio.h>
int p[20]={2,3,5,7,11,13,17,19,23,29,31,37,41,43,47,53,59};
int main()
{
double N;
while (scanf("%lf",&N)!=EOF)
{
__int64 ans=0;
int i,j;
for (i=0;i<17;i++)
{
int m=(int)pow(N,1.0/p[i]);
while (pow(m+1,p[i])<=N) m++;
ans+=m-1;
}
for (i=0;i<10;i++)
for (j=i+1;j<10;j++)
if (p[i]*p[j]<60)
{
int m=(int)pow(N,1.0/(p[i]*p[j]));
while (pow(m+1,p[i]*p[j])<=N) m++;
ans-=m-1;
}
if(N>=pow(2,30))ans++;
if(N>=pow(2,42))ans++;
if(N>=pow(3,30))ans++;
printf("%I64d
",ans+1);
}
return 0;
}
