Preliminaries for Benelux Algorithm Programming Contest 2019： I. Inquiry I

论算法优化的重要性

要有分析算法时间复杂度的潜意识，慢慢培养。

别总是上来暴力，还有可怕的两层循环2333qwq

The Bureau for Artificial Problems in Competitions wants you to solve the following problem: Given n positive integers a1, . . . , an, what is the maximal value of 

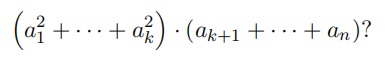
Input: 

• A single line containing an integer 2 ≤ n ≤ 10^6. 

• Then follow n lines, the ith of which contains the integer 1 ≤ ai ≤ 100.

Output:

 Output the maximal value of the given expression.

样例输入1复制

5
2
1
4
3
5

样例输出1复制

168

样例输入2复制

2
1
1

样例输出2复制

1

样例输入3复制

10
8
5
10
9
1
4
12
6
3
13

样例输出3复制

10530
分析：我一上来就是两层循环直接暴力，然后2000ms直接TLE了，接着优化一下输入输出1995ms，继续tle，最后靠着fy大佬帮我优化代码，

我最初tle的代码：

#include<iostream>
#include<cstdio>
using namespace std;
typedef long long ll;
ll n;//n要设为全局变量2333，要不然不能输入啦 
int a[1000006];
int main()
{
	scanf("%lld",&n);
	for(int i=1;i<=n;i++)
	{
		scanf("%d",&a[i]);	
	}
	//k  [1,n-1]
	ll maxval=0;
	int k,i;
	
	for(k=1;k<=n-1;k++)
	{
		ll p=0,q=0;
		for(i=1;i<=k;i++)
		{
			p+=a[i]*a[i];
		}
		for(i=k+1;i<=n;i++)
		{
			q+=a[i];
		}
		maxval=max(p*q,maxval);
	}
	
	printf("%lld
",maxval);
}
//TLE了qwq 
//优化过后从2000ms到1995ms，qwq
//tle了太卑微了qwq 
//我这是单纯的暴力 

　优化后成功AC的代码：

#include<iostream>
#include<cstdio>
using namespace std;
typedef long long ll;
ll n;
int a[1000006];
ll f1[1000006]={0};
ll f2[1000006]={0};
int main()
{
	scanf("%lld",&n);
	for(int i=1;i<=n;i++)
	{
		scanf("%d",&a[i]);
		f2[0]+=a[i];	
	}
	
	for(int k=1;k<=n-1;k++)
	{
		f1[k]=f1[k-1]+a[k]*a[k];
		f2[k]=f2[k-1]-a[k];
	}
	
	ll maxval=0;
	for(int k=1;k<=n-1;k++)
	{
		maxval=max(maxval,f1[k]*f2[k]);
	}
	
	printf("%lld
",maxval);
}//这样时间就得到了顺利的优化2333
//在法人的帮助下成功ac了，法人say:要有这个潜意识,慢慢培养 
//运行时间和编译时间是不搭边的吧2333 
//"我想想，能不能化简一下公式"进行算法复杂度分析 

　　提供的标程代码：

/*
求公式最大值
*/
#include <cstdio>
#include <cstring>
#include <cmath>
#include <cctype>
#include <iostream>
#include <algorithm>
#include <map>
#include <set>
#include <vector>
#include <string>
#include <stack>
#include <queue>

typedef long long LL;
using namespace std;

int n, a[1000005];
LL l[1000005], r[1000005];

int main()
{
	//freopen("in.txt", "r", stdin);
	//freopen("out.txt", "w", stdout);

	scanf("%d", &n);
	for (int i = 1; i <= n; i++) scanf("%d", &a[i]);
	for (int i = 1; i <= n; i++) l[i] = l[i - 1] + a[i] * a[i];
	for (int i = n; i >= 1; i--) r[i] = r[i + 1] + a[i];
	LL ans = 0;
	for (int i = 1; i < n; i++) ans = max(ans, l[i] * r[i + 1]);
	printf("%lld
", ans);

	return 0;
}
/**/