一些借鉴截图如下:
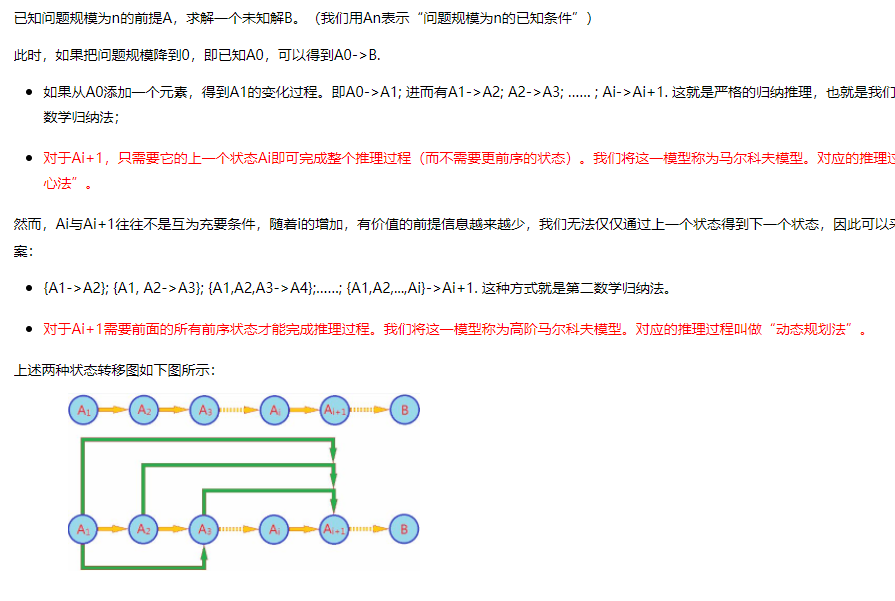
能用动态规划解决的问题的特点:
(1)最优化原理:如果问题的最优解所包含的子问题的解也是最优的,就称该问题具有最优子结构,即满足最优化原理。
(2) 无后效性:即某阶段状态一旦确定,就不受这个状态以后决策的影响。也就是说,某状态以后的过程不会影响以前的状态,只与当前状态有关。
(3)有重叠子问题:即子问题之间是不独立的,一个子问题在下一阶段决策中可能被多次使用到。(该性质并不是动态规划适用的必要条件,但是如果没有这条性质,动态规划算法同其他算法相比就不具备优势)



Problem 1:打土豪,分田地。

thoughts analysis:
题目意思是把这块地分16份,但是当不是4*4的其他情况的矩阵的时候,就有多种切分的情况,每种情况牛牛都会有最小的一块地,这里就有多种最小的情况,然后从这多种最小的情况下,找到最大的一个情况!
my code:
#include<bits/stdc++.h>
using namespace std;
char str[110];//numberic strings.数字字符
int a[110][110];//数字矩阵number matrix
int sum[110][110],n,m;
int calc(int x,int y,int i,int j)//起点:(i,j),终点:(x,y).
{
return sum[x][y]+sum[i][j]-sum[x][j]-sum[i][y];
}//求取左上顶点(i,j)到右下顶点(x,y)确定的矩形田地的价值和
bool judge(int x)
{
for(int i=1;i<=m-3;i++)
{
for(int j=i+1;j<=m-2;j++)
{
for(int k=j+1;k<=m-1;k++)
{
int last=0,cnt=0;
for(int r=1;r<=n;r++)
{
int s1=calc(r,i,last,0);
int s2=calc(r,j,last,i);
int s3=calc(r,k,last,j);
int s4=calc(r,m,last,k);
if(s1>=x&&s2>=x&&s3>=x&&s4>=x)//当前横一刀满足条件。
{
last=r;cnt++;
}
}
if(cnt>=4) return true;//表明当前x是16块田地中最小的,返回true
}
}
}
return false;
}
int main()
{
while(scanf("%d%d",&n,&m)>0)
{
for(int i=1;i<=n;i++)
{
scanf("%s",str+1);//从str[1]开始哦。
for(int j=1;j<=m;j++) a[i][j]=str[j]-'0';
}
memset(sum,0,sizeof(sum));
for(int i=1;i<=n;i++)
{
for(int j=1;j<=m;j++)
{
sum[i][j]=sum[i-1][j]+sum[i][j-1]-sum[i-1][j-1]+a[i][j];
}
}//sum[i][j]表示坐标(i,j)左上方价值总和
int l=0,r=sum[n][m],ans=0;//二分
while(l<=r)
{
int mid=(l+r)>>1;
if(judge(mid))
{
l=mid+1;
ans=mid;
}
else
{
r=mid-1;
}
}
printf("%d
",ans);
}
return 0;
}
链接:https://www.nowcoder.com/practice/fe30a13b5fb84b339cb6cb3f70dca699?tpId=85&&tqId=29833&rp=1&ru=/activity/oj&qru=/ta/2017test/question-ranking
拓展引发的基础性的思考积累:
eg:将n个长度为m的字符串转换为数字矩阵。
一种代码如下:
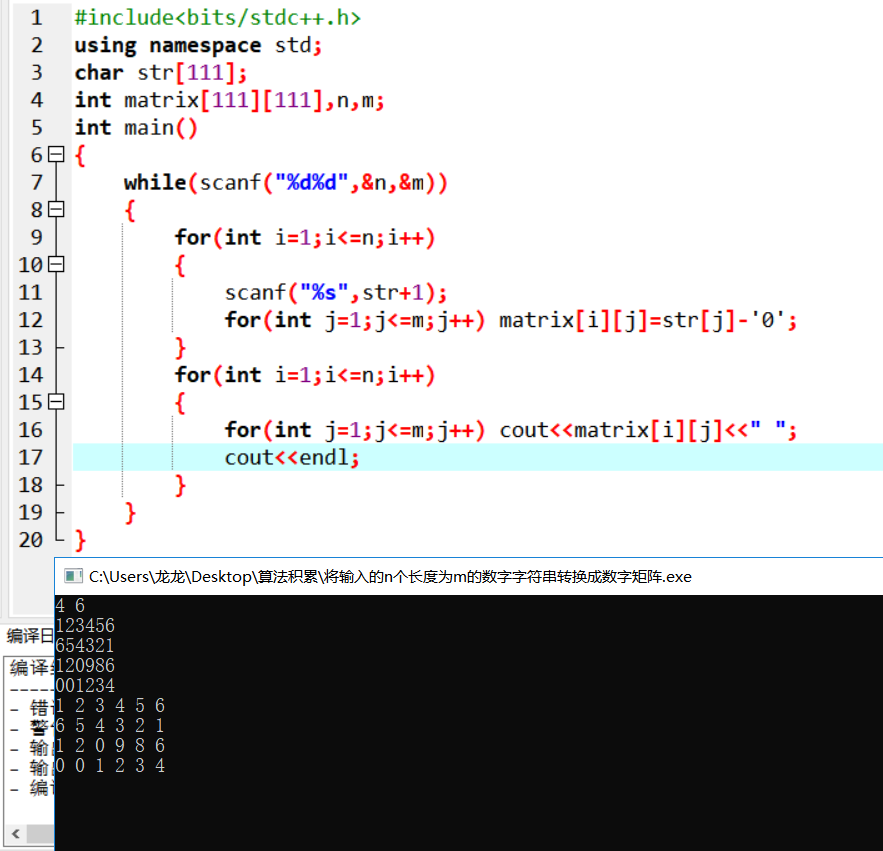
And a question:
