2017-2018 ACM-ICPC Northern Eurasia (Northeastern European Regional) Contest (NEERC 17)
A
题意:有 n 个时刻,第 i 个时刻要么会在 (xi,yi) 生成一个半径为 yi 的圆,要么射击 (xi,yi) 这个点,如果该点在某个圆内则把对应圆删除并输出该圆的标号,否则输出 -1 。任意时刻圆之间不会相交(可以相切)。 (n le 2*10^5, -10^9 le x_i,y_i le 10^9, y_i > 0)
key:线段树,结论
结论:与一条竖线相交的圆的个数不超过 (O(log max y_i)) 个。
证明:可以证明下图中,两圆的半径比是 4。也就是说最差时半径以4倍增长。
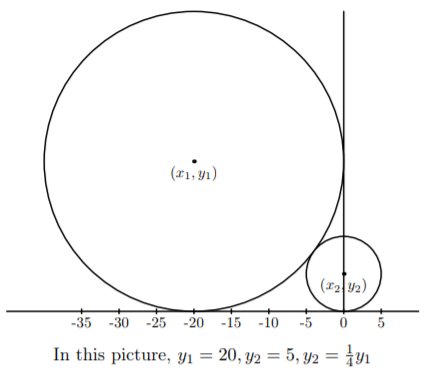
所以每次只需要找到覆盖该竖线的所有圆,然后一个个check即可。可以用线段树维护。
当一个圆插入时,它覆盖的区间最大为 ((x_i-y_i,x_i+y_i)) 。以查找直线左边的圆为例,只要在 (x_i) 处把 (x_i+y_i) 插入,之后询问时递归直线左半边,如果区间最大值比 (x_i) 小则直接 return。递归到叶子时计算是否可行。
因为至多递归到 log 个叶子,所以总复杂度是 (O(nlog n log max y_i))
仔细观察可以发现实际上只有 i+k*m 这个集合中的点有边,并且形成了一个环,而环的大小就是集合中 1 的个数。
I
题意:一个随机排列,偶数按顺序放到 e 数组中,奇数按顺序放到 o 数组中。每次可以询问 (e_i) 和 (o_j) 的大小关系。求在 (3*10^5) 的询问数下输出 e 和 o 。 (n le 10000)
key:排序,交互
考虑快排:每次把区间分为两段。
枚举 o 中的每个数,此时考虑有若干段区间,该数一定存在在某个区间中间(或者是 1 或 n,这个要特判)。由于区间之间存在有序性,所以可以先对所有区间二分,此时该数只会落在两个区间内,然后再从两个区间里暴力判断。由于是随机排列,所以可以证明总询问数是 (O(n log n))
L
题意:给出树上 m 条路径,询问是否有两条路径相交(包含不算)。 (n,m le 2*10^5)
key:树剖,随机权值
考虑路径覆盖。相离好说,现在问题是如何把相交和包含区分出来。
考虑相交:即做路径覆盖时,被覆盖的每一个点的覆盖状态一致(都没被覆盖/都被某些路径覆盖),否则就一定存在相交。
为了在每个点上保存“被覆盖的状态”,容易想到哈希。实际上只要给每个路径附一个随机的权值,那样可以认为在做的过程中它们任意两个集合的权值异或和不相同(虽然所有集合的异或和肯定有相同的,但是算法执行过程中不会遍历太多的集合)。此时覆盖一条路径时只需要每个点异或上该路径的权值即可。