排序算法分析

1. 冒泡排序(平均时间复杂度O(n^2), 辅助空间O(1), 稳定排序)

主要思想: 两两比较相邻记录的关键字值，如果是反序则交换，直到没有反序记录为止。

 1 #include <iostream>
 2 #include <ctime >
 3 #include <algorithm>
 4 #include <vector>
 5 using namespace std;
 6 
 7 template<typename T>
 8 void BubbleSort(vector<T>& data, unsigned size)
 9 {
10     bool ordered;
11     for (unsigned i = 0; i < size - 1; i++)   //外层循环 -- 一共进行比较的趟数( size - 1 ) 
12     {
13         ordered = true;                       //每趟需要比较的次数 
14         for (unsigned j = 0; j < size - i - 1; j++) {
15             //每次选出  当前位置元素  应当所在的  最大位置, 并交换 
16             if (data[j] > data[j + 1]) {
17                 swap(data[j], data[j + 1]);
18                 ordered = false;             //只要交换，则说明交换前，不是有序 
19             }
20         }
21         if (ordered) {                       //一次交换都没有，说明已经没有逆序对，则已经有序，直接退出循环！ 
22             break;
23         }
24     }
25 }
26 
27 int main()
28 {
29     vector<int> data;               // = {6, 4, 16, 9 , 8 , 2, 11, 5, 12, 45, 3, 19, 34, 23};
30     srand(unsigned(time(NULL)));
31     
32     int cnt = 10;
33     while (cnt--) {
34         for (int i = 0; i < 20; i++) {
35             data.push_back(rand() % 100);
36         }
37         unsigned len = data.size();
38     
39         for (auto i : data)
40             cout << i << " ";
41 
42         cout << endl;
43 
44         BubbleSort(data, len);
45     
46         for (auto i : data) 
47             cout << i << " ";
48         cout << endl;
49         cout << "#############################################

";
50         data.clear();
51     }
52     return 0;
53 
54 }

2. 插入排序 (平均时间复杂度O(n^2)，辅助空间O(1)，稳定排序)

基本思想:依次把待排序序列中的每一个记录插入到一个已经排序好的序列中，直到全部记录都排序好。

最好情况下（待排序序列为正序），时间复杂度为O（n^2）

 1 #include <iostream>
 2 #include <ctime>
 3 #include <vector>
 4 using namespace std;
 5 
 6 template<typename Comparable>
 7 void InsertSort(vector<Comparable>& data, unsigned size)
 8 {
 9     int j;
10     
11     for ( int p = 1; p < data.size(); p++ ) {          //从第二个数开始 
12         Comparable tmp = data[p];
13         for ( j = p; j > 0 && tmp < data[j - 1]; j-- ) 
14             data[j] = data[j - 1];                    //将比tmp大的数字，逐个后移 
15         data[j] = tmp;                                //将tmp插入到，第一个 或是 第一个比他小的数前面 
16     }
17 }
18 
19 int main()
20 {
21     vector<int> data;               // = {6, 4, 16, 9 , 8 , 2, 11, 5, 12, 45, 3, 19, 34, 23};
22     srand(unsigned(time(NULL)));
23 
24     int cnt = 10;
25     while (cnt--) {
26         for (int i = 0; i < 20; i++) {
27             data.push_back(rand() % 100);
28         }
29         unsigned len = data.size();
30     
31         for (auto i : data)
32             cout << i << " ";
33 
34         cout << endl;
35 
36         InsertSort(data, len);
37     
38         for (auto i : data) 
39             cout << i << " ";
40         cout << endl;
41         cout << "#############################################

";
42         data.clear();
43     }
44     
45     return 0;
46 
47 }

3.选择排序(时间复杂度O(n^2), 辅助空间O(1)，不稳定排序)

主要思想是：每一趟从待排序中选取一个关键字最小的记录，也即第一趟中从n个记录中选取关键字最小的记录，第二趟从剩下n-1个记录中选取关键字最小的记录。直到整个序列记录选完。这样，由选取记录的顺序，便得到按关键字有序序列。

 1 #include <iostream>
 2 #include <ctime>
 3 #include <vector>
 4 using namespace std;
 5 
 6 template<typename T>
 7 void ChooseSort(vector<T>& data, unsigned size)
 8 {
 9     int k = 0, i, j;
10     T tmp = 0;
11     for (i = 0; i < size - 1; i++) 
12     {
13         k = i;          //此假设为最小值下标
14         for (j = k+1; j < size; j++) {
15             if (data[k] > data[j]) {
16                 k = j;  //找出下一个开始的最小的下标 
17             }
18         }
19         //如果假设的最小的下标改变了,就将最小下标位置元素
20         //与i位置交换，则i为当前位置最小的元素 
21         if (i != k) {    
22             tmp = data[i];
23             data[i] = data[k];
24             data[k] = tmp;
25         }
26     }
27 }
28 
29 int main()
30 {
31     vector<int> data;               // = {6, 4, 16, 9 , 8 , 2, 11, 5, 12, 45, 3, 19, 34, 23};
32     srand(unsigned(time(NULL)));
33 
34     int cnt = 10;
35     while (cnt--) {
36         for (int i = 0; i < 20; i++) {
37             data.push_back(rand() % 100);
38         }
39         unsigned len = data.size();
40     
41         for (auto i : data)
42             cout << i << " ";
43 
44         cout << endl;
45 
46         ChooseSort(data, len);
47     
48         for (auto i : data) 
49             cout << i << " ";
50         cout << endl;
51         cout << "#############################################

";
52         data.clear();
53     }
54     
55     return 0;
56 
57 }

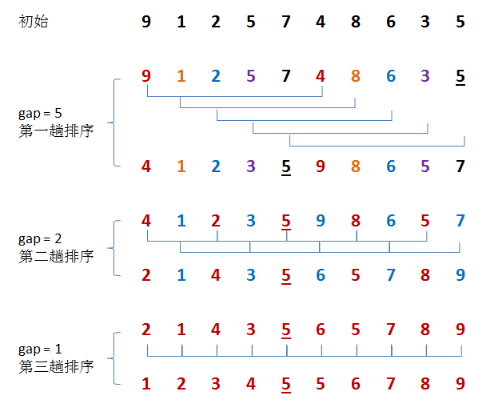
4.希尔排序(ShellSort, 亚二次时间(最坏O（N^(4/3)）, 辅助空间O(1)，不稳定排序）

主要思想: 相当于插入排序的升级, 通过比较相距一定间隔的元素来工作; 各趟比较所用的距离随着算法的进行二减小, 直到比较相邻元素的最后一趟排序为止。（缩减增加排序）。ShellSort需要使用一个序列h1, h2......,ht, 叫做增量序列。只要h1 = 1，任何增量序列都是可行的(h1 = 1时，相当于插入排序)

 1 #include <iostream>
 2 #include <ctime>
 3 #include <vector>
 4 using namespace std;
 5 
 6 //ShellSort -- 不稳定排序 
 7 //适用于 大量输入数据 的时候 
 8 template<typename Comparable>
 9 void ShellSort(vector<Comparable>& data)
10 {
11     //1 9 2 10 3 11 4 12 5 13 6 14 7 15 8 16  -- 此为时间不好的情形 
12     for (int gap = data.size() / 2; gap > 0; gap /= 2)       //Shell增量初始为size的一半, 
13     {
14         for (int i = gap; i < data.size(); i++) {            //gap相当于 待插入数 开始的位置 
15             Comparable tmp = data[ i ];                      //取出 待插入 数 
16             int j = i;                                       //获得 待插入数的 索引 
17             //如果  j小于了gap(待插入元素已经与首个元素比较了) 或是 待插入数大于 前面比较的元素
18             //就退出循环.
19             //否则,如果 待插入数  大于 前面比较的 元素， 就交换他 与 比较的元素
20             //每次 循环, 待插入数索引 j 向前移动 gap 位置
21             for ( ; j >= gap && tmp < data[ j - gap ]; j -= gap )
22                 data[ j ] = data[ j - gap ];
23             data[ j ] = tmp;                                 //插入 待插入元素 
24         }
25     }    
26 }
27 
28 int main()
29 {
30     vector<int> data;               
31     srand(unsigned(time(NULL)));
32 
33     int cnt = 10;
34     while (cnt--) {
35         for (int i = 0; i < 20; i++) {
36             data.push_back(rand() % 100);
37         }
38     
39         for (auto i : data)
40             cout << i << " ";
41 
42         cout << endl;
43 
44         ShellSort(data);
45     
46         for (auto i : data) 
47             cout << i << " ";
48         cout << endl;
49         cout << "#############################################

";
50         data.clear();
51     }
52     
53     return 0;
54 
55 }

5.堆排序(平均时间复杂度O(nlogn), 空间复杂度（O(1)，不稳定排序）

主要思想：实现一个（max）堆（线性时间）, 然后通过将堆中的最后元素与第一个元素交换，缩减堆的大小并进行下滤，来执行N-1次deleteMax操作。当算法终止时，数组则以所排的顺序包含这些元素。

 1 #include <iostream>
 2 #include <ctime>
 3 #include <vector>
 4 using namespace std;
 5 
 6 /** 堆排序 
 7  *  比 ShellSort 慢，即使带有明显紧凑内循环的O(NlogN) 
 8  * 不适合少量数据的排序 
 9  */
10 
11 /**
12  * Internal method for HeadSort
13  * i is the Index of item in the Heap.
14  * Return the index of the left child.(得到i索引(结点)的左孩子在数组中的索引)
15  * 首先要知道, 树在数组中表示的时候，i 的 左孩子索引为 i * 2  
16  */
17 inline int leftChild( int i )
18 {
19     return 2 * i;
20 }
21 
22 /**
23  * Interanl method for HeadSort that is used in deleteMax and buildHeap. 
24  * i is the position from which to percolate(过滤,渗出) down.
25  * n is the logical size of the binary Heap.
26  * 此为建立大顶堆过程,  亦是对(每次删除Max,用来调整位置--使每次处于大顶堆 位置) 
27  */
28 template<typename Comparable>
29 void percDown ( vector<Comparable> & a, int i, int n )
30 {
31     int child;
32     Comparable tmp;
33     
34     // tmp-父亲结点; 左结点的索引 < n ;  继续 判断孩子结点 
35     for ( tmp = a[i]; leftChild( i ) < n; i = child ) { 
36         child = leftChild( i );      //获得左孩子结点索引 
37         //如果孩子结点索引 尚未越界, 且  左孩子结点 小于 右孩子 结点 
38         if ( child != n - 1 && a[ child ] < a[ child + 1 ] ) 
39             child++;                 //就获得右孩子结点索引 
40         if ( tmp < a[ child ] )      //父亲 < 孩子 
41             a[ i ] = a[ child ];     //孩子 替换 父亲结点 
42         else                        
43             break;
44     }
45     a[ i ] = tmp;                    //将父亲结点 插入 到比他大的 孩子结点位置.
46 }
47 
48 /* HeapSort -- 不稳定排序
49  * 排序的稳定性 是指如果在排序的序列中，存在前后相同的两个
50  * 元素的话, 排序前 和 排序后 他们的相对位置不发生变化
51  */
52 template<typename Comparable>
53 void HeapSort(vector<Comparable>& a)
54 {
55     for ( int i = a.size() / 2; i >= 0; i-- ) {      // Build Heap
56         percDown( a, i, a.size() );                  // 从 size/2 开始建堆(这里为大顶堆) 
57     }
58     for ( int j = a.size() - 1; j > 0; j-- ) {
59         swap( a[0], a[j] );                         // Delete Max(a[0]始终为 未有序数中的最大值) 
60         percDown( a, 0, j );                        //并调整位置(调整为大顶堆) 
61     }
62 }
63 
64 int main()
65 {
66     vector<int> data;             
67     srand(unsigned(time(NULL)));    
68 
69     int cnt = 10;
70     while (cnt--) {
71         for (int i = 0; i < 20; i++) {
72             data.push_back(rand() % 100);
73         }
74     
75         for (auto i : data)
76             cout << i << " ";
77 
78         cout << endl;
79 
80         HeapSort(data);
81     
82         for (auto i : data) 
83             cout << i << " ";
84         cout << endl;
85         cout << "#############################################

";
86         data.clear();
87     }
88     
89     return 0;
90 
91 }

6.归并排序（时间复杂度O(nlogn)，辅助空间O（n），稳定排序）

主要思想：合并两个已排序的表，递归操作，典型的分而治之

  1 #include <iostream>
  2 #include <ctime>
  3 #include <vector>
  4 using namespace std;
  5 
  6 /**
  7  * 归并排序，使用了最少次数的比较，运行时间很大程度依赖于数组中进行元素比较和移动所消耗的时间 
  8  * Java 中, 归并排序是一般目的排序的最佳排序(Java中元素比较耗时多, 移动快)
  9  * 但是, c++中，复制代价很大, 所以归并排序 不是非常适合c++ 
 10  */
 11 
 12 //函数声明 
 13 template<typename Comparable>
 14 void MergeSort( vector<Comparable>& a );
 15 
 16 template <typename Comparable>
 17 void MergeSort( vector<Comparable> & a, 
 18                 vector<Comparable> & tmpArray, int left, int right );
 19 
 20 template <typename Comparable>
 21 void merge ( vector<Comparable> & a, vector<Comparable> & tmpArray,
 22              int leftPos, int rightPos, int rightEnd );
 23 
 24 //implement
 25 template<typename Comparable>
 26 void MergeSort( vector<Comparable>& a )
 27 {
 28     vector<Comparable> tmpArray( a.size() );
 29     MergeSort( a, tmpArray, 0, a.size() - 1);
 30 }
 31 
 39 template <typename Comparable>
 40 void MergeSort( vector<Comparable> & a, 
 41                 vector<Comparable> & tmpArray, int left, int right )
 42 {
 43     if ( left < right ) 
 44     {
 45         int center = ( left + right ) / 2;
 46         MergeSort( a, tmpArray, left, center );
 47         MergeSort( a, tmpArray, center + 1, right );
 48         merge( a, tmpArray, left, center + 1, right );
 49     }
 50 }
 51 
 52 /***
 53  * Internal method that merges two sorted halves(两等分) of a subarray.
 54  * a is an array of Comparable items. (待排序数组)
 55  * tmpArray is an array to place the merged result.(存放合并后数组)
 56  * leftPos is the left-most index of the subarray. (左子序列的开始下标)
 57  * rightPos is the index of the start of the second half.(右子序列的开始下标)
 58  * rightEnd is the right-most index of the subarray.(右子序列的结束位置)
 59  */
 60 template <typename Comparable>
 61 void merge ( vector<Comparable> & a, vector<Comparable> & tmpArray,
 62              int leftPos, int rightPos, int rightEnd )
 63 {
 64     int leftEnd = rightPos - 1;                //左子序列 结束位置
 65     int tmpPos = leftPos;                      //左子序列开始位置-用来存放 合并数组 的 下标增量
 66     int numElements = rightEnd - leftPos + 1;  //元素总数: End - Start + 1
 67 
 68     //Main loop
 69     // 左右子序列都没有遍历结束
 70     while ( leftPos <= leftEnd && rightPos <= rightEnd ) {
 71         if ( a[ leftPos ] <= a[ rightPos ])        //left <= right
 72             tmpArray[ tmpPos++ ] = a[ leftPos++ ]; //Copy left to tmpArray 
 73         else
 74             tmpArray[ tmpPos++ ] = a[ rightPos++ ];
 75     }
 76 
 77     while ( leftPos <= leftEnd )               //如果是右子序列先结束
 78         tmpArray[ tmpPos++ ] = a[ leftPos++ ]; //就将左子序列元素全部放进归并数组
 79 
 80     while ( rightPos <= rightEnd )             //Copy rest of right half
 81         tmpArray[ tmpPos++ ] = a[ rightPos++ ];
 82 
 83     //Copy tmpArray back(将暂存有序元素的数组,复制到原来的数组中)
 84     for ( int i = 0; i < numElements; ++i, rightEnd-- ) {
 85         a[ rightEnd ] = tmpArray[ rightEnd ];
 86     }
 87 }
 88 
 89 
 90 int main()
 91 {
 92     vector<int> data;              
 93     srand(unsigned(time(NULL)));
 94 
 95     int cnt = 10;
 96     while (cnt--) {
 97         for (int i = 0; i < 20; i++) {
 98             data.push_back(rand() % 100);
 99         }
100     
101         for (auto i : data)
102             cout << i << " ";
103 
104         cout << endl;
105 
106         MergeSort(data);
107     
108         for (auto i : data) 
109             cout << i << " ";
110         cout << endl;
111         cout << "#############################################

";
112         data.clear();
113     }
114     
115     return 0;
116 
117 }

7.快速排序（平均时间复杂度O(nlogn), 最坏情况O（n^2））

主要思想：

（1）如果S中元素个数是0或1，则返回

（2）取S中任一元素v，称之为枢纽元（pivot）

（3）将S-{v}（S中其余元素）划分成两个不相交的集合: S1={x∈S-{v}|x<=v}和S2={x∈S-{v}|x>=v}。

（4）返回{quickSort(S1),后跟v，继而quickSort(S2)}.

注：7.1.有点类似于二叉排序树，最终某对于枢纽元，他左子树的所有元素都小于他，他右子树的所有元素都大于他。

7.2.需要递归实现。

　　7.3 对于枢纽元的选择也十分重要，这里采取的是三数中值分割法(a[left[ < a[center] < a[right]（需要适当的进行排序）

  1 #include <iostream>
  2 #include <ctime>
  3 #include <vector>
  4 using namespace std;
  5 
  6 
  7 /**
  8  * 快排的思路: 
  9  * 1. 选择一个枢纽pivot, 然后 让它左边的数都小于他，让他右面的数都大于他。 
 10  * 2. 然后递归, 在左边的子序列中, 重复1的过程. 在右面的子序列中, 重复1的过程
 11  * 3. 就像是排序二叉树形成的过程那样. 左子树结点小于所有的祖宗结点, 右子树大于所有祖宗结点 
 12  */
 13  
 14 /* ============================== Decalation =====================================*/ 
 15 /***
 16  * Return median of left, center, and right
 17  * Order these and hide the pivot --- 用来求 枢纽数 
 18  */
 19 template <typename Comparable>
 20 const Comparable & median3( vector<Comparable> & a, int left, int right );
 21 
 22 /**
 23  * QuickSort algorithm (driver) -- 快排的驱动程序 
 24  */
 25 template<typename Comparable>
 26 void QuickSort( vector<Comparable> & a );
 27 
 28 /**
 29  * Internal quickSort method that makes recursive calls/
 30  * Uses median-of-three partitioning and a curoff of 10.(使用三数中值分割法和截止范围10，
 31  * 截止范围即使在排序数量在 N<=10时,使用插入排序.N > 10才使用快排)
 32  * a is array of Comparable items.
 33  * left is the left-most index of the subarray.
 34  * right is the right-most index of the subarray.
 35  */
 36 template<typename Comparable>
 37 void QuickSort ( vector<Comparable> & a, int left, int right );
 38 
 39 template<typename Comparable>
 40 void InsertSort(vector<Comparable>& data, int left, int right );
 41 
 42 
 43 //Implement
 44 template <typename Comparable>
 45 const Comparable & median3( vector<Comparable> & a, int left, int right )
 46 {
 47     int center = ( left + right ) / 2;
 48     if ( a[ center ] < a[ left ])
 49         swap( a[left ], a[ center ] );    
 50     if ( a[ right ] < a[ left ])
 51         swap( a[ left ], a[ right ] ); 
 52     if ( a[ right ] < a[ center ])
 53         swap( a[ center ], a[ right ]);  
 54 
 55     // a[left] < a[center] < a[right]
 56 
 57     //place pivot at position right - 1
 58     swap( a[ center ], a[ right - 1] );    //与 right - 1的元素交换
 59     return a[ right - 1 ];                 //返回 枢纽值 
 60 }
 61 
 62 //left--指向第一个数, right-指向最后一个元素 
 63 template <typename Comparable>
 64 void QuickSort( vector<Comparable> & a, int left, int right )
 65 {
 66     if ( left + 10 <= right )              //对范围10以内的数, 进行插入排序 
 67     {
 68         Comparable pivot = median3( a, left , right );  //找出枢纽值
 69 
 70         //Begin partitioning(两等分) 
 71         int i = left, j = right - 1;      //初始化为 比他们 正确值+1, 使不存在考虑特殊情况 
 72         for ( ; ; )
 73         {
 74             while ( a[ ++i ] < pivot ) {}               // i 移过小元素,指向大元素 
 75             while ( pivot < a[ --j ] ) {}               // j 移过大元素,指向小元素 
 76             if ( i < j ) {                              //如果没有交错, 就交换他们的值(这里直接交换效率高) 
 77                 int tmp = a[i];
 78                 a[i] = a[j];
 79                 a[j] = tmp; 
 80             }                  
 81             else                                       //当i, j相遇. 就退出循环 
 82                 break;
 83         }
 84         //如今, i 位置 左边 元素都 小于它, j 位置都 大于它 
 85         swap( a[ i ], a[ right - 1 ] );    //Restore pivot -- 更新枢纽(现在i指向小元素) 
 86 
 87         QuickSort( a, left, i - 1 );       //Sort small elements
 88         QuickSort( a, i + 1, right );      //Sort large elements
 89     }  
 90     else
 91         InsertSort( a, left, right );      //对小数组用插入排序,效率更高 ! 
 92 }
 93 
 94 template <typename Comparable>  
 95 void InsertSort(vector<Comparable>& a,int left,int right)  
 96 {  
 97     int j;  
 98   
 99       for ( int p = left + 1; p <= right; p++ ) 
100       {
101           Comparable tmp = a[p];
102           
103         for ( j = p; j > left && tmp < a[ j - 1 ]; j-- )    
104             a[ j ] = a[ j - 1 ];
105         a[ j ] = tmp;
106     }
107 }  
108 
109 template<typename Comparable>
110 void QuickSort( vector<Comparable> & a )
111 {
112     QuickSort( a, 0, a.size() - 1);    //传递, 被排序数组范围(left,right)
113 }
114 
115 int main()
116 {
117     vector<int> data;              
118 //    srand(unsigned(time(NULL)));
119 
120     int cnt = 10;
121     while (cnt--) {
122         
123         cout << "Test " << cnt << ": "<< endl;
124         for (int i = 0; i < 30; i++) {
125             data.push_back(rand() % 100);
126         }
127     
128         for (auto i : data)
129             cout << i << " ";
130 
131         cout << endl;
132 
133         QuickSort(data);
134     
135         for (auto i : data) 
136             cout << i << " ";
137         cout << endl;
138         cout << "#############################################

";
139         data.clear();
140     }
141     
142     return 0;
143 
144 }

总结：（使用的建议）

1. 使用c++，对于最一般的内部排序应用，选用方法（插入排序，希尔排序，快速排序）。

2. 快速排序，即使对于很少的输入数据也能和谢尔排序一样快。快速排序的改进仍然有O（N^2）的最坏情形，但是这种最坏情形出现的机会是微不足道的，以至于不能成为影响算法的因素。如果需要对大量数据排序，那么快速排序则是应该选择的排序方法。但是，永远不要为省事，而轻易的把第一个元素用作枢纽元。

3. 如果你不想考虑上面的问题，就使用谢尔排序，谢尔排序有些小缺陷，不过可以接受，特别需要简单明了的时候。谢尔排序的最坏情形也只不过是O(N^(4/3))，这种最坏发生的几率也是微不足道的。

4.堆排序要比谢尔排序慢，尽管它是一个带有明显紧凑内循环的O（NlogN）。但是，为了移动数据，堆排序需要进行两次比较。（Floyd提出改进算法移动数据，只需要一次比较，但是代码会更复杂）

5.插入排序，用于在小或是基本上排好序的数据上。

6.没有提到归并排序（虽然它运行时间O(NlogN)）但是很难用于主存排序，不如快速排序那么好) （ps: 合并是外部排序的中心思想），主要问题在与合并两个排序的表需要线性附加内存，在整个算法中还要花费将数据复制到临时数组再复制回来的附加工作，严重影响速度。不过，在Java语言中，当排序为一般对象时，元素的比较耗时很多，但是移动元素很快，且所有排序中，归并排序使用最少次数的比较。因此，在Java中，归并是一般目的排序的最佳选择。然而，c++中，对于一般排序，当对象很大时，复制对象的代价是很大的，而对象的比较通常相对消耗少些。

相关阅读:
引领5G行业化，广和通荣获“IoT创新大奖”
Win知识
 物联网通信方式
 萌新配置rip动态路由实验
 FPGA设计经验总结
 UWB定位技术
 REST简介
 linux性能调优总结
 Nginx安装及启动
 leetcode 精选top面试题
原文地址：https://www.cnblogs.com/douzujun/p/6170691.html