https://www.bilibili.com/video/BV1G54y1971S?from=search&seid=14148477947249263260
https://zhuanlan.zhihu.com/p/133282394
简介


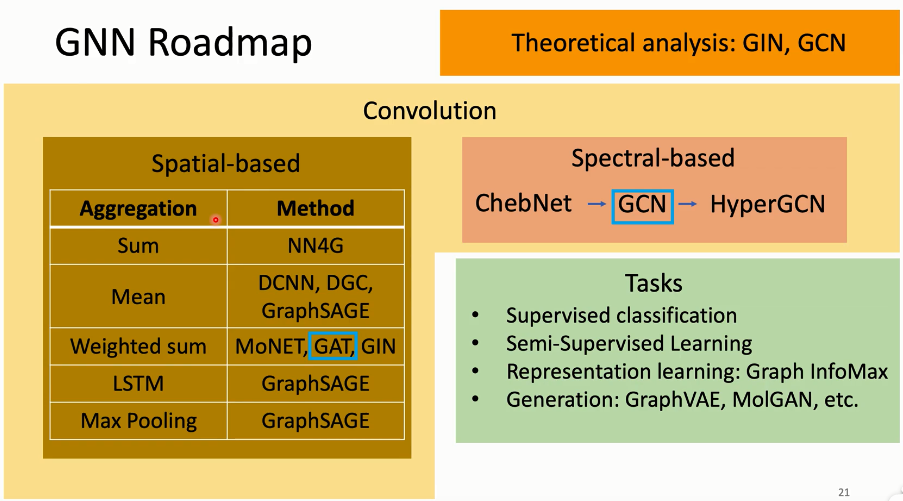

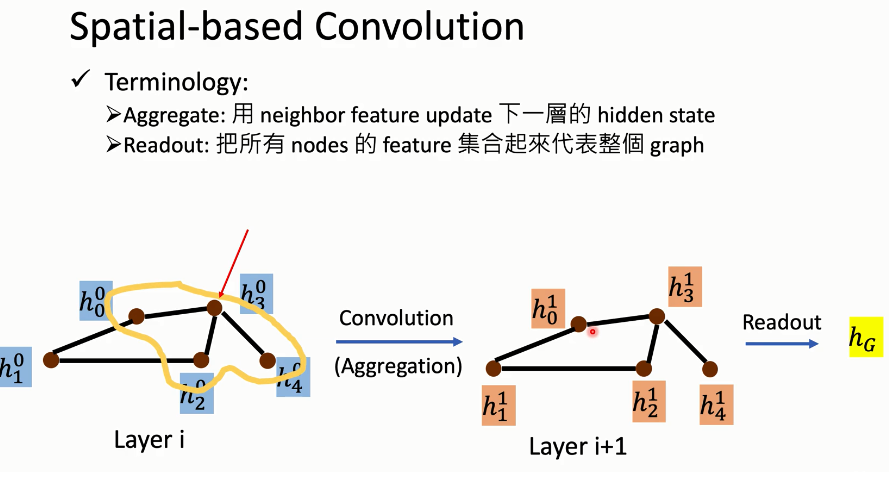
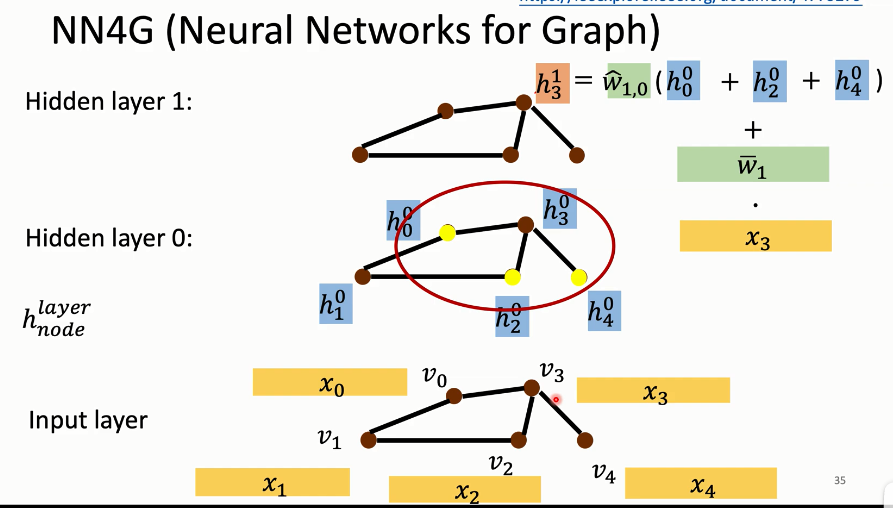
Spatial-based(基于空间的)



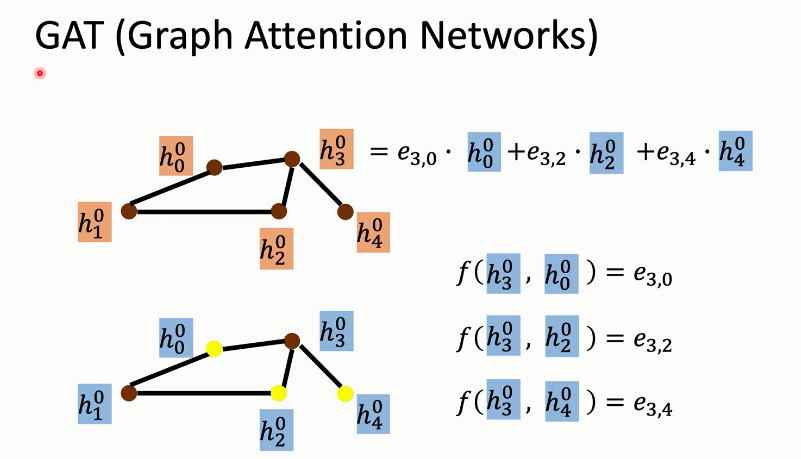
GAT(Graph Attention Networks)

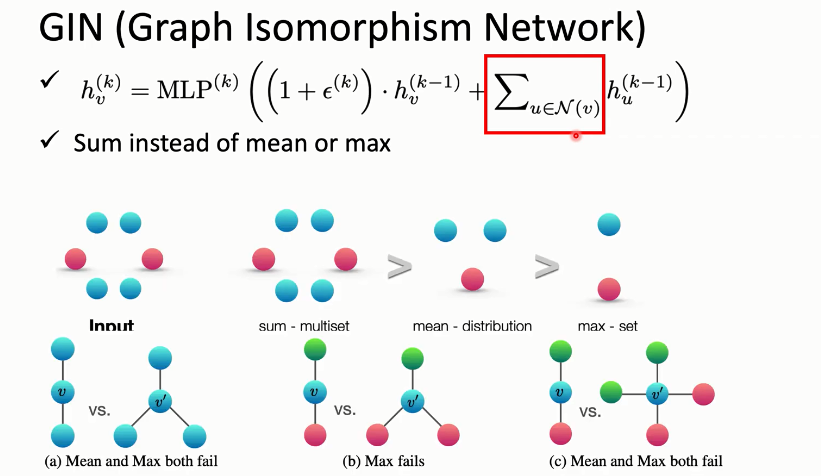
GIN(Graph Isomorphism Network)


Spectral-based(基于频谱)
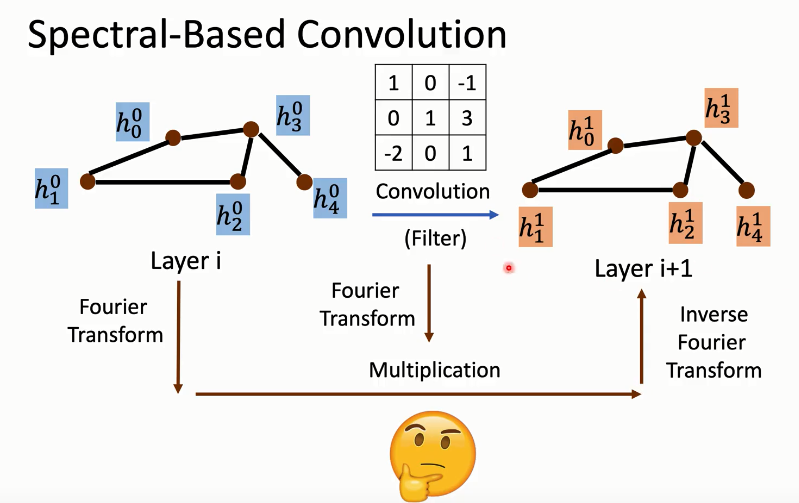
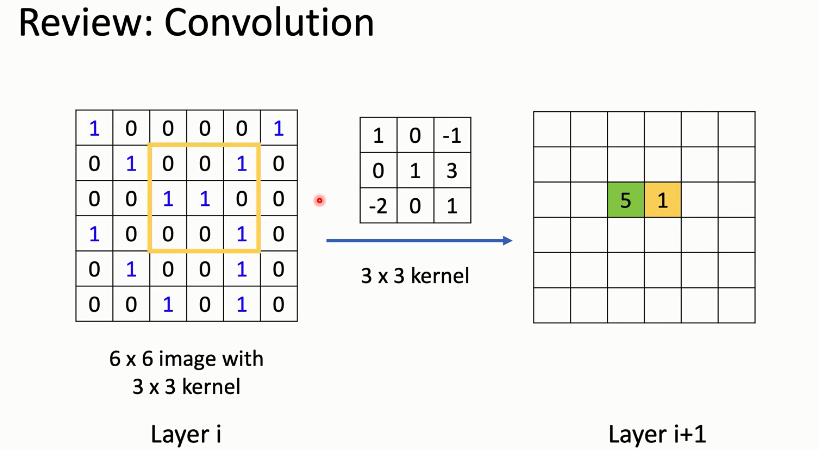
另一种给图做卷积的思路是,我们尝试把一个图上的信号(把特征看作是信号),通过傅里叶变换到频域空间,乘上频域空间上的卷积核,再傅里叶逆变换回来。
在讲频域卷积之前,我们需要补充一些《信号与系统》的知识。

信号可以看作是一种 N-维空间的向量。这个向量是由一组基向量通过线性组合合成的。
当我们想知道它里面每个不同的部分的权重 (a_k),我们就需要分析。分析方式是我们用这个向量 A 与 A 中的某个特定成分做内积,得到 (a_j) 。

以上是在空间域上的,基向量一般是空间坐标轴 x, y, z。在频域上的基向量一般为 cos 和 sin。


关于傅里叶变换视频。
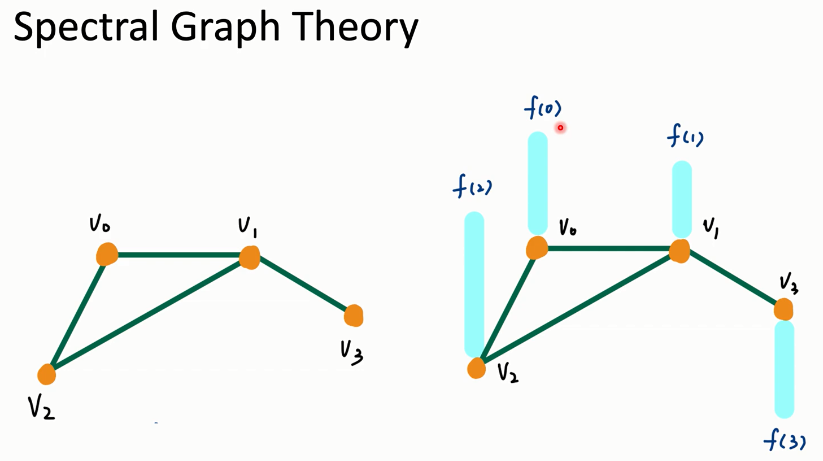
Spectral Graph Theory
图结构为节点信号在空间上的关系。我们可以把这个空间上的图转换为频域上的图。
对这个图的频谱进行滤波操作后,再转换回空间上的图,就可以实现卷积过程。我们要如何把空间上的图变成频域上的图呢?这里需要了解一下谱图理论。

一个图我们会用邻接矩阵 (A) 来表示。 (A_{i,j}) 的值为节点 i 和节点 j 的距离权重。我们只考虑无向图。我们再用 (D) 来表示度矩阵。
度为一个节点与它的邻居的权重边之和。 (f(x)) 用来表示节点 x 上的信号。
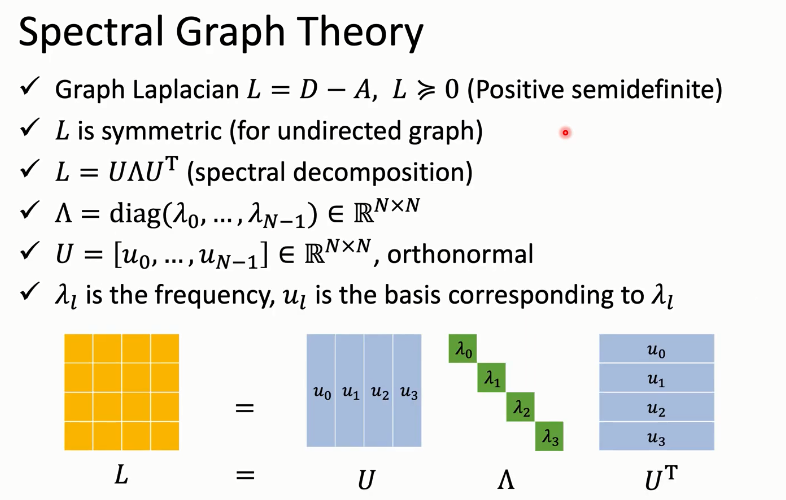
图拉普拉斯矩阵被定义为 (L = D - A)。(L) 的定义保证了它是半正定的。无向图保证了 (L) 是对称的。
这样我们就可以对矩阵 (L) 做特征值分解。(L) 可以分解成 (Lambda^{T})。
(Lambda) 是一个全为 (lambda{i}) 的对角矩阵,(U) 为有向量 (u_i) 组成的正交矩阵。(lambda_i)为频率,(u_i)为该频率对应的基。

该图是一个获得 (L, Lambda) 和 (U) 的例子。
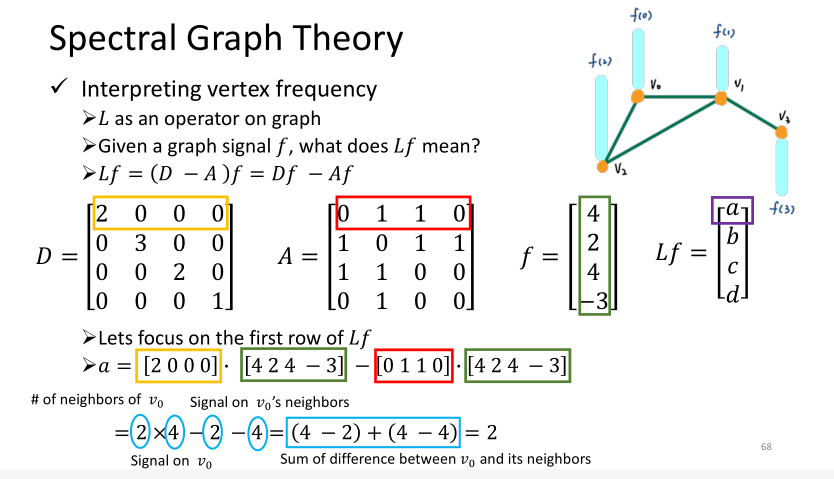
我们可以把 L 当作是一个用来对图操作的矩阵。给定一个图的信号f,用 L 与它相乘,Lf = (D-A)f = Df - Af。
它所做的操作刚好等价于当前节点与它周边邻居的能量差异之和。频率越大,相邻节点的能量变化也就越大。
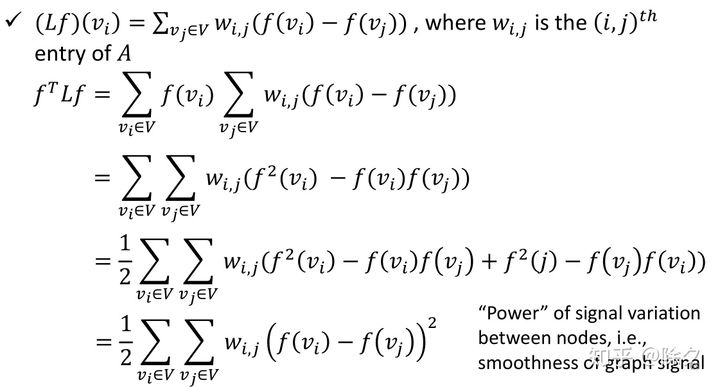
如果我们让 Lf 再乘上当前节点vi,推导化简下来,会得到该节点与周边节点的信号能量差的加权求和。
我们就可以用这个计算的结果来 量化某个图信号的频域大小 是多少。
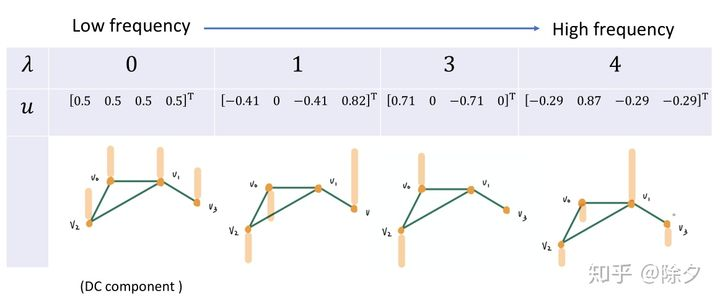
这就是图傅里叶变换.它做的是让图映射到频域上。当我们的图信号越平滑,相邻两个节点信号的差异会越小。反之图信号越不平滑,相邻两个节点信号的差异就会越大。
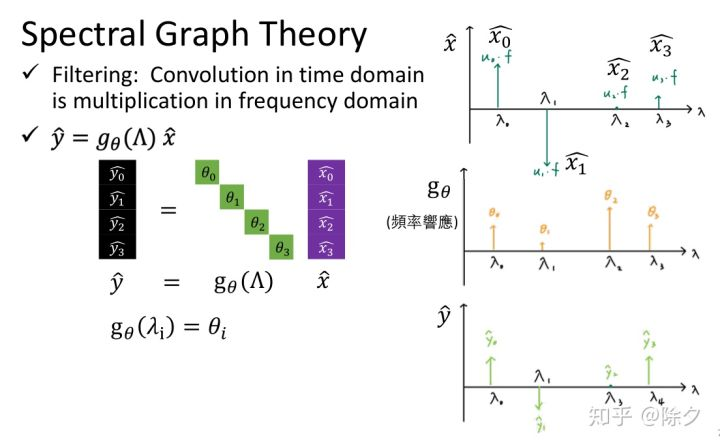
神经网络的权重也可以用相同的方法转到频域上。二者相乘就完成了滤波操作。
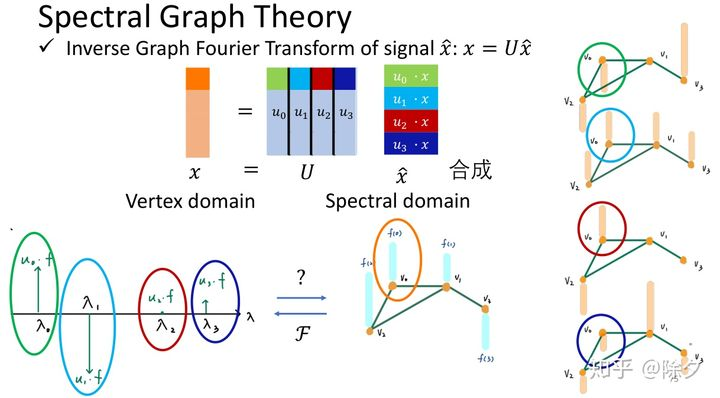
我们要如何把频域的图转换回来呢?直接把某个节点上的频率U 和其能量大小相乘,再加权求和。
