1. 动机一:数据压缩
第二种类型的 无监督学习问题,称为 降维。有几个不同的的原因使你可能想要做降维。一是数据压缩,数据压缩不仅允许我们压缩数据,因而使用较少的计算机内存或磁盘空间,但它也让我们加快我们的学习算法。
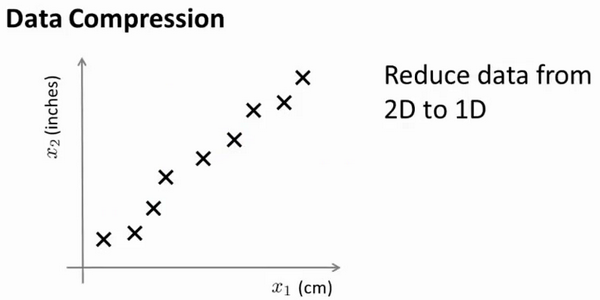
但首先,让我们谈论 降维是什么。作为一种生动的例子,我们收集的数据集,有许多,许多特征,我绘制两个在这里。
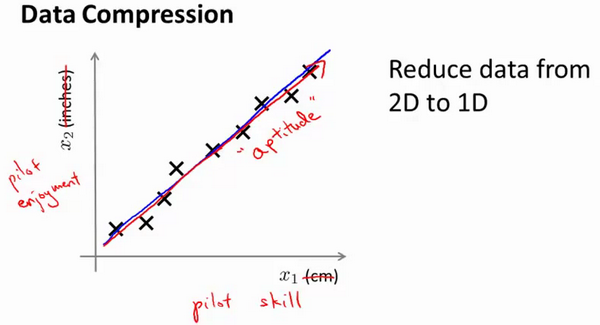
将数据从二维降一维:

将数据从三维降至二维: 这个例子中我们要将一个三维的特征向量降至一个二维的特征向量。过程是与上面类似的,我们将三维向量投射到一个二维的平面上,强迫使得所有的数据都在同一个平面上,降至二维的特征向量。
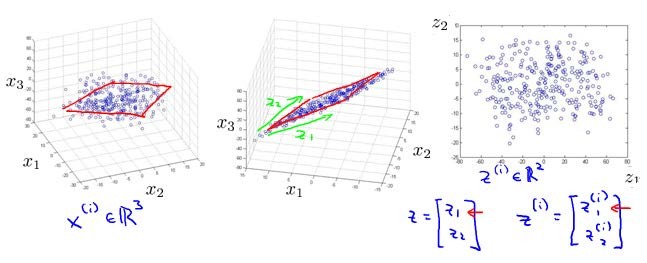
这样的处理过程可以被用于把任何维度的数据降到任何想要的维度,例如将1000维的特征降至100维。
2. 动机二:数据可视化
在许多及其学习问题中,如果我们能将数据可视化,我们便能寻找到一个更好的解决方案,降维可以帮助我们。
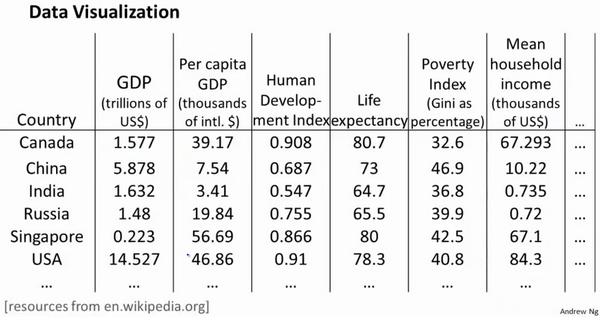
假使我们有有关于许多不同国家的数据,每一个特征向量都有50个特征(如GDP,人均GDP,平均寿命等)。
如果要将这个50维的数据可视化是不可能的。使用降维的方法将其降至2维,我们便可以将其可视化了。
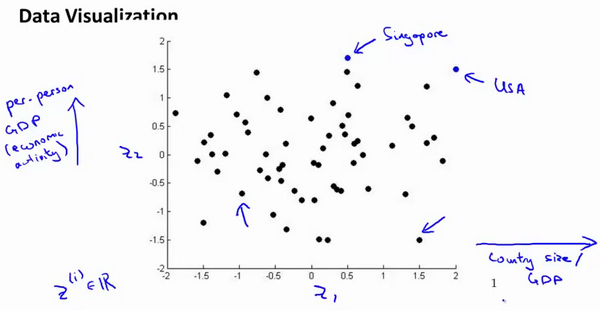
这样做的问题在于,降维的算法只负责减少维数,新产生的特征的意义就必须由我们自己去发现了。
3. 主成分分析问题
-
主成分分析(PCA)是最常见的降维算法。
-
在PCA中,我们要做的是找到一个方向向量(Vector direction),当我们把所有的数据都投射到该向量上时,我们希望 投射平均均方误差 能尽可能地小。
-
方向向量:是一个经过原点的向量,而 投射误差 是 从特征向量 向该方向向量作垂线的长度。
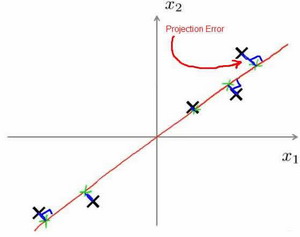
下面给出主成分分析问题的描述:
-
问题:将n维数据降至k维,目标是找到向量 $u^{(1)},u^{(2)},...,u^{(k)}$ 使得 总的投射误差最小。主成分分析与线性回顾的比较:
-
主成分分析与线性回归是两种不同的算法。主成分分析最小化的是 投射误差(Projected Error),而线性回归尝试的是最小化:预测误差。线性回归的目的是 预测结果,而主成分分析 不作任何预测。
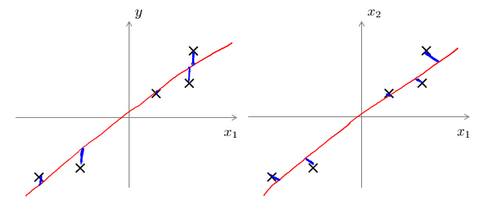
上图中,左边的是线性回归的误差(垂直于横轴投影),右边则是主要成分分析的误差(垂直于红线投影)。
-
PCA:将n个特征降维到k个,可以用来进行数据压缩,如果100维的向量最后可以用10维来表示,那么压缩率为90%。同样图像处理领域的KL变换使用PCA做图像压缩。但PCA 要保证降维后,还要保证数据的特性损失最小。
-
PCA技术好处:是对数据进行降维的处理。我们可以对新求出的“主元”向量的重要性进行排序,根据需要取前面最重要的部分,将后面的维数省去,可以达到降维从而简化模型或是对数据进行压缩的效果。同时最大程度的保持了原有数据的信息。
-
PCA技术优点:它是完全无参数限制的。在PCA的计算过程中完全不需要人为的设定参数 或是 根据任何经验模型对计算进行干预,最后的 结果只与数据相关,与用户是独立的。
-
但是,这一点同时也可以看作是缺点。如果用户对观测对象有一定的先验知识,掌握了数据的一些特征,却无法通过参数化等方法对处理过程进行干预,可能会得不到预期的效果,效率也不高。
-
第一步:均值归一化。
- 我们需要计算出所有特征的均值,然后令 $x_j= x_j-μ_j$。如果特征是在不同的数量级上,我们还需要将其除以 标准差 $σ^2$。
-
第二步:计算 协方差矩阵(covariance matrix)Σ:
- $sum=dfrac {1}{m}sum^{n}_{i=1}left( x^{(i)} ight) left( x^{(i)} ight) ^{T}$
-
第三步:计算 协方差矩阵Σ 的 特征向量(eigenvectors):
-
在 Matlab 里我们可以利用 奇异值分解(singular value decomposition)来求解,[U, S, V]= svd(sigma) 。
-

