约瑟夫问题
约瑟夫问题是个著名的问题:N个人围成一圈,第一个人从1开始报数,报M的将被杀掉,下一个人接着从1开始报。如此反复,最后剩下一个,求最后的胜利者。
例如只有三个人,把他们叫做A、B、C,他们围成一圈,从A开始报数,假设报2的人被杀掉。
首先A开始报数,他报1。侥幸逃过一劫。
然后轮到B报数,他报2。非常惨,他被杀了
C接着从1开始报数
接着轮到A报数,他报2。也被杀死了。
最终胜利者是C
解决方案
普通解法
刚学数据结构的时候,我们可能用链表的方法去模拟这个过程,N个人看作是N个链表节点,节点1指向节点2,节点2指向节点3,……,节点N-1指向节点N,节点N指向节点1,这样就形成了一个环。然后从节点1开始1、2、3……往下报数,每报到M,就把那个节点从环上删除。下一个节点接着从1开始报数。最终链表仅剩一个节点。它就是最终的胜利者。
缺点:
要模拟整个游戏过程,时间复杂度高达O(nm),当n,m非常大(例如上百万,上千万)的时候,几乎是没有办法在短时间内出结果的。
公式法
约瑟夫环是一个经典的数学问题,我们不难发现这样的依次报数,似乎有规律可循。为了方便导出递推式,我们重新定义一下题目。
问题: N个人编号为1,2,……,N,依次报数,每报到M时,杀掉那个人,求最后胜利者的编号。
这边我们先把结论抛出了。之后带领大家一步一步的理解这个公式是什么来的。
递推公式:
f(N,M)=(f(N−1,M)+M)%N
f(N,M)=(f(N−1,M)+M)%N
f(N,M)f(N,M)表示,N个人报数,每报到M时杀掉那个人,最终胜利者的编号
f(N−1,M)f(N−1,M)表示,N-1个人报数,每报到M时杀掉那个人,最终胜利者的编号
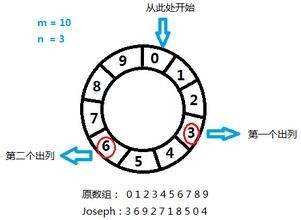
下面我们不用字母表示每一个人,而用数字。
1、2、3、4、5、6、7、8、9、10、11
1、2、3、4、5、6、7、8、9、10、11
表示11个人,他们先排成一排,假设每报到3的人被杀掉。
刚开始时,头一个人编号是1,从他开始报数,第一轮被杀掉的是编号3的人。
编号4的人从1开始重新报数,这时候我们可以认为编号4这个人是队伍的头。第二轮被杀掉的是编号6的人。
编号7的人开始重新报数,这时候我们可以认为编号7这个人是队伍的头。第三轮被杀掉的是编号9的人。
……
第九轮时,编号2的人开始重新报数,这时候我们可以认为编号2这个人是队伍的头。这轮被杀掉的是编号8的人。
下一个人还是编号为2的人,他从1开始报数,不幸的是他在这轮被杀掉了。
最后的胜利者是编号为7的人。
下图表示这一过程:
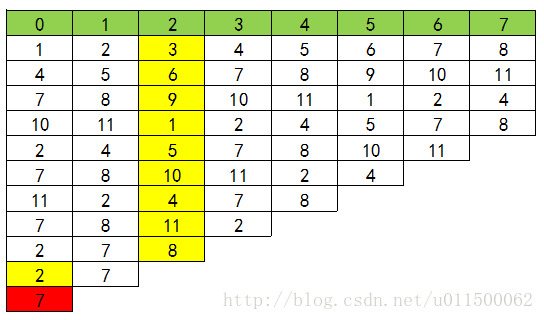
现在再来看我们递推公式是怎么得到的!
将上面表格的每一行看成数组,这个公式描述的是:幸存者在这一轮的下标位置
f(1,3):只有1个人了,那个人就是获胜者,他的下标位置是0
f(2,3)=(f(1,3)+3)%2=3%2=1f(2,3)=(f(1,3)+3)%2=3%2=1:在有2个人的时候,胜利者的下标位置为1
f(3,3)=(f(2,3)+3)%3=4%3=1f(3,3)=(f(2,3)+3)%3=4%3=1:在有3个人的时候,胜利者的下标位置为1
f(4,3)=(f(3,3)+3)%4=4%4=0f(4,3)=(f(3,3)+3)%4=4%4=0:在有4个人的时候,胜利者的下标位置为0
……
f(11,3)=6f(11,3)=6
很神奇吧!现在你还怀疑这个公式的正确性吗?上面这个例子验证了这个递推公式的确可以计算出胜利者的下标,下面将讲解怎么推导这个公式。
问题1:假设我们已经知道11个人时,胜利者的下标位置为6。那下一轮10个人时,胜利者的下标位置为多少?
答:其实吧,第一轮删掉编号为3的人后,之后的人都往前面移动了3位,胜利这也往前移动了3位,所以他的下标位置由6变成3。
问题2:假设我们已经知道10个人时,胜利者的下标位置为3。那下一轮11个人时,胜利者的下标位置为多少?
答:这可以看错是上一个问题的逆过程,大家都往后移动3位,所以f(11,3)=f(10,3)+3f(11,3)=f(10,3)+3。不过有可能数组会越界,所以最后模上当前人数的个数,f(11,3)=(f(10,3)+3)%11f(11,3)=(f(10,3)+3)%11
问题3:现在改为人数改为N,报到M时,把那个人杀掉,那么数组是怎么移动的?
答:每杀掉一个人,下一个人成为头,相当于把数组向前移动M位。若已知N-1个人时,胜利者的下标位置位f(N−1,M)f(N−1,M),则N个人的时候,就是往后移动M为,(因为有可能数组越界,超过的部分会被接到头上,所以还要模N),既f(N,M)=(f(N−1,M)+M)%nf(N,M)=(f(N−1,M)+M)%n
注:理解这个递推式的核心在于关注胜利者的下标位置是怎么变的。每杀掉一个人,其实就是把这个数组向前移动了M位。然后逆过来,就可以得到这个递推式。
因为求出的结果是数组中的下标,最终的编号还要加1
java代码实现如下:
public Node josephusKill(Node head,int m){ if(head == null || head.next ==head|| m<1){ return head; } Node cur = head.next; int tmp = 1; while(cur != head){ tmp ++; cur = cur.next; } tmp = getLive(tmp,m); while(--tmp != 0){ head = head.next; } head.next = head; return head; } public int getlive(int n,int m){ if(n ==1){ return 1; } return (getlive(int n-1,int m)+m)%n; }
本文参考博客:https://blog.csdn.net/u011500062/article/details/72855826