预测赢家

重新做一遍，两个月前做的已经忘记的差不多了。。。

给定一个表示分数的非负整数数组。 玩家 1 从数组任意一端拿取一个分数，随后玩家 2 继续从剩余数组任意一端拿取分数，然后玩家 1 拿，…… 。每次一个玩家只能拿取一个分数，分数被拿取之后不再可取。直到没有剩余分数可取时游戏结束。最终获得分数总和最多的玩家获胜。

给定一个表示分数的数组，预测玩家1是否会成为赢家。你可以假设每个玩家的玩法都会使他的分数最大化。

输入：[1, 5, 2]
输出：False
解释：一开始，玩家1可以从1和2中进行选择。
如果他选择 2（或者 1 ），那么玩家 2 可以从 1（或者 2 ）和 5 中进行选择。如果玩家 2 选择了 5 ，那么玩家 1 则只剩下 1（或者 2 ）可选。
所以，玩家 1 的最终分数为 1 + 2 = 3，而玩家 2 为 5 。
因此，玩家 1 永远不会成为赢家，返回 False 

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/predict-the-winner

这道题很有意思，因为这涉及到一点博弈的感觉，一开始接触总觉得无处下手。看完答案之后我只能说，妙极了。

这道题考虑的动态规划的求解，那么如何来定义base case，以及状态转移方程呢？

首先，先引入另一道题887.石子游戏，这是预测赢家的一个特例，它多了两个限制条件，1.数组长度为偶数 2.数组加和为奇数（一定有一个人赢）

这个题，只用一步就能求解，很有意思。

class Solution {
public:
    bool stoneGame(vector<int>& piles) {
        return true;
    }
};

这里有些数学的东西，很好玩。

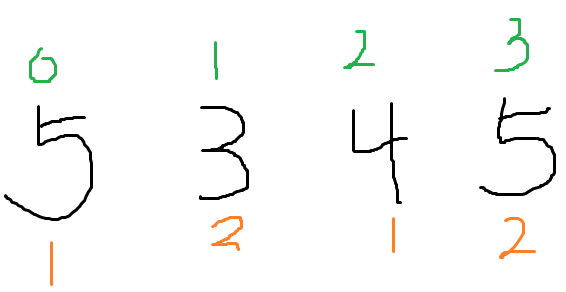
如图，4堆石子，分成两组，偶数为1，奇数为2.

玩家1先手，判断玩家1是不是能赢。首先玩家1可以选择1或者2，如果选择了1，则玩家2只能从2中选一个，接下来玩家1又能从1，2进行选择。

所以玩家1可以选择同一组，而玩家1完全可以通过计算哪一组的加和更大，选择哪一组，这样必然会胜利。

故，回到这一题，我们可以知道，当数组长度为偶数时 return true;

我们考虑奇数的情况

dp[i][j]表示子数组[i...j]中的最大得分（不区分玩家1和玩家2，因为每一位玩家都是想得到最大分数的）

那么对于数组只有一个元素时，dp[i][i]=num[i];

状态转移方程：dp[i][j],可以选择num[i],temp1=num[i]-dp[i+1][j]//减去玩家2的分数；选择num[j],temp2=num[j]-dp[i][j-1]

故dp[i][j]=max(temp1,temp2)

所以我们的代码为：

class Solution {
public:
    bool PredictTheWinner(vector<int>& nums) {
        //dp table
        int n=nums.size();
        if(n%2==0||n==0)
            return true;
        int dp[n][n];
        for(int i=0;i<n;i++)
            dp[i][i]=nums[i];
        for(int i=n-2;i>=0;i--){
            for(int j=i+1;j<n;j++){
                dp[i][j]=max((nums[i]-dp[i+1][j]),(nums[j]-dp[i][j-1]));
            }
        }
        return dp[0][n-1]>=0;
    }
};