跳跃游戏1，2

我又懈怠了。。。新的一天重新刷题

关于跳跃游戏两则：

第一个是leetcode 55题

给定一个非负整数数组，你最初位于数组的第一个位置。

数组中的每个元素代表你在该位置可以跳跃的最大长度。

判断你是否能够到达最后一个位置。

输入: [2,3,1,1,4]
输出: true
解释: 我们可以先跳 1 步，从位置 0 到达 位置 1, 然后再从位置 1 跳 3 步到达最后一个位置。

问题是判断，能否到达最后一个位置，那么只要我们跳跃的最大长度大于数组长度，那么就一定可以到达最后一个位置。

求解：

class Solution {
public:
    bool canJump(vector<int>& nums) 
    {
        int n = nums.size();
        int longest= 0;
        for (int i = 0; i < n; ++i) 
        {
            if (i <= longest) 
                longest = max(longest, i + nums[i]);
                if (longest >= n - 1) 
                    return true;
        }
        return false;
    }
};

跳跃游戏2

给定一个非负整数数组，你最初位于数组的第一个位置。

数组中的每个元素代表你在该位置可以跳跃的最大长度。

你的目标是使用最少的跳跃次数到达数组的最后一个位置。

输入: [2,3,1,1,4]
输出: 2
解释: 跳到最后一个位置的最小跳跃数是 2。
     从下标为 0 跳到下标为 1 的位置，跳 1 步，然后跳 3 步到达数组的最后一个位置。

不同点：保证能跳跃到最后一个位置，求最少的跳跃数

可以选择用动态规划，但是这里可以考虑一下贪心选择

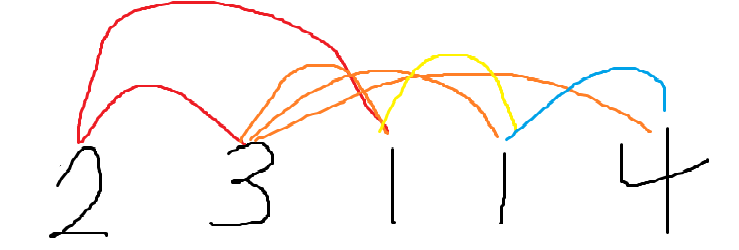
如图所示，第一个位置0处，可以跳到0+1,0+2处，step+1; 当跳到0+1处，下一步可以跳到0+1++,0+1+2,0+1+3处, step+1; 每一次都判断能否到达最后一个位置，如果到达则return;

具体实现如下：

class Solution {
public:
    int jump(vector<int>& nums) {
        int steps = 0;
        int start = 0;
        int end = 0;
        while (end < nums.size()-1) {
            int max = end;
            for (int i = start; i <= end; i++) {//选一个最有潜力的
                if (nums[i]+i > max) {
                    max = nums[i]+i;
                } 
            }
            start = end+1;
            end = max;
            steps++;
        }
        return steps;
    }
};