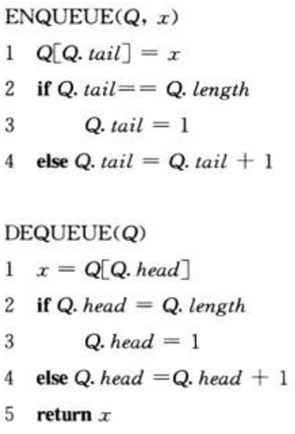基本数据结构(1)——算法导论(11)

1. 引言

    从这篇博客开始，来介绍一些基本的数据结构知识。本篇及下一篇会介绍几种基本的数据结构：栈、队列、链表和有根树。此外还会介绍由数组构造对象和指针的方法。

    这一篇主要介绍栈和队列，它们都是动态集合。

    从数据的逻辑结构上讲，在它们上进行delete操作所移除的元素是固定的：在栈（stack）中，被删除的是最近插入的元素（后进先出，LIFO，last-in，first-out）；而在队列（queue）中，被删除的元素是最先插入的元素（先进先出，FIFO，first-in，first-out）。

    从数据的存储结构上讲，它们都可以用顺序结构存储和链式结构存储来实现（虽然在之后的图中，在形式上是以数组的方式画出的）。

2. 栈(stack)

     在栈上的insert操作被称为push（压入，压栈），而delete操作被称为pop（弹出，出栈）。在现实生活中有许多与栈类似的“结构”。如一个弹夹（后被塞入弹夹的子弹先被打出），一摞堆叠的盘子（我们每次只能取出最上面的盘子）等等。

    如下图，是一个栈S在进行push和pop操作时的示意图。栈有一个属性top（栈顶指针），用来标记（指向）栈顶元素。注意：有时候我们在实现push或者pop操作时，不一定真的要在物理存储结构上添加或移除某个元素（因为这会带来额外的开销，当然有必要做时要做），而是可以通过移动栈顶指针来实现。

    如果在栈中不包含任何元素，我们称栈是空（empty）的；如果试图对一个空栈进行pop操作，则称栈下溢（underflow）；相反，如果试图对一个大小固定为n，且top已经指向了位置n的栈进行push操作时，则称栈上溢（overflow）；

    下面给出实现栈的伪代码（没有考虑栈的上溢问题）：

    栈的一个经典的应用就是检索一串只包含正反括号的字符串中的正反括号是否匹配（这里匹配的概念是：就像我们在写代码时，正反括号不管如何层层嵌套，都必须正反匹配）。具体的做法是：我们遍历待检索的字符串，遇到正括号就把正括号push入栈，遇到反括号就对栈进行pop操作。若在遍历过程中遇到栈下溢错误或遍历完成后栈不为空则字符串中的正反括号是不匹配的；否则是匹配的。

下面给出Java实现代码：

public class Main11 {
    public static void main(String[] args) {
        System.out.println(checkBrackets("()((())"));
        System.out.println(checkBrackets("())(())"));
        System.out.println(checkBrackets("()(())"));
    }

    /**
     * 检查str中的括号是否匹配
     * 
     * @param str
     * @return
     */
    public static boolean checkBrackets(String str) {
        if (str == null || str.isEmpty()) {
            throw new NullPointerException("待检测的字符串不能为空");
        }
        if (!str.matches("[\(\)]+")) {
            throw new RuntimeException("待检测的字符不能包含除'(',')'以外的字符");
        }
        Stack<Character> stack = new Stack<Character>();
        for (int i = 0; i < str.length(); i++) {
            char c = str.charAt(i);
            if (c == '(') {
                stack.push(c);
            } else {
                try {
                    stack.pop();
                } catch (Exception e) {
                    return false;
                }
            }
        }
        return stack.isEmpty();
    }
}

/**
 * <p>
 * 栈
 * </p>
 * <p>
 * 这里只是对LinkedList作简单的封装来模拟一个栈结构
 * </p>
 * 
 * @author D.K
 *
 * @param <T>
 */
class Stack<T> {
    private LinkedList<T> list;

    public Stack() {
        list = new LinkedList<>();
    }

    public boolean isEmpty() {
        return list.isEmpty();
    }

    public void push(T t) {
        list.addLast(t);
    }

    public T pop() {
        return list.removeLast();
    }
}

结果：

3. 队列(queue)

   在队列上的insert操作被称为enqueue（入队），而delete被称为dequeue（出对）。在现实生活中，我们在购物结账时所排的队就像队列数据结构一样（先到的人排在对列的前面，先结账，先离开）。

    如下图，描述的是队列Q在进行enqueue和dequeue操作的过程。队列有head（对头）和tail（队尾）。队列中的元素存放在Q.head与Q.tail-1之间。队列是首尾相连（环绕）的。初始时，Q.head = Q.tail = 1。当Q.head = Q.tail时，队列是空的，如果试图从空队列中删除一个元素，则发生队列下溢；当Q.head = Q.tail+1时，队列是满的，如果试图在满队列插入一个元素，则发生队列上溢。

    下面给出队列实现的伪代码（省略了溢出检查）

    下面我们来看一个应用队列的例子。（例子借鉴自：http://www.cnblogs.com/shenliang123/archive/2013/02/16/2913552.html）

    在密码学中，恺撒密码是一种最简单且最广为人知的加密技术。据传是古罗马恺撒大帝用来保护重要军情的加密系统（不太可信）。它的具体做法是，将待加密的英文字符串的每个字母以字母表的顺序移动一定的位数来实现加密。这是很容易被破解的，因为移动的方案只有25种（假设每个字母移动相同的位数）。

    现在我们来考虑一个类似但稍微靠谱点加密方式（其实通过对字母出现频率的统计还是很容易破译）。我们先事约定一组密钥（用队列来存放），然后把每个字符按字母表顺序向右移动密钥中对应位置上的数。下面给出Java实现代码：

public class Main11_2 {

    public static final Integer[] SECRET_KEY = new Integer[] { -1, 3, 2, 5, 9, 0 };

    public static void main(String[] args) {
        String originaltext = "good good study,day day up!";
        System.out.println("原文是：" + originaltext);
        // 加密
        String ciphertext = encrypt(originaltext);
        System.out.println("密文是：" + ciphertext);
        // 解密
        String plaintext = decrypt(ciphertext);
        System.out.println("明文是：" + plaintext);
    }

    /**
     * 加密
     * 
     * @param plaintext
     *            明文
     * @return 密文
     */
    private static String encrypt(String plaintext) {
        String ciphertext = "";
        if (plaintext == null || plaintext.isEmpty()) {
            return ciphertext;
        }
        Queue<Integer> queue = new Queue<>(SECRET_KEY);
        for (int i = 0; i < plaintext.length(); i++) {
            char c = plaintext.charAt(i);
            int key = queue.dequeue();
            ciphertext += (char) (c + key);
            queue.enqueue(key);
        }
        return ciphertext;
    }

    /**
     * 解密
     * 
     * @param ciphertext
     *            密文
     * @return 明文
     */
    private static String decrypt(String ciphertext) {
        String plaintext = "";
        if (ciphertext == null || ciphertext.isEmpty()) {
            return plaintext;
        }
        Queue<Integer> queue = new Queue<>(SECRET_KEY);
        for (int i = 0; i < ciphertext.length(); i++) {
            char c = ciphertext.charAt(i);
            int key = queue.dequeue();
            plaintext += (char) (c - key);
            queue.enqueue(key);
        }
        return plaintext;
    }
}

class Queue<E> {

    private LinkedList<E> list;

    public Queue() {
        this(null);
    }

    public Queue(E[] objs) {
        list = new LinkedList<>();
        if (objs != null) {
            for (E e : objs) {
                enqueue(e);
            }
        }
    }

    public boolean isEmpty() {
        return list.isEmpty();
    }

    public void enqueue(E e) {
        list.addLast(e);
    }

    public E dequeue() {
        return list.removeFirst();
    }
}

结果：