函数的增长——算法导论(2)

1. 引言

   这一章主要是介绍一些概念，虽然很乏味，但是它确实能够帮助我们去更好的分析、处理问题。

2. 渐进记号

（1） θ 记号

      在上一章中，我们记插入排序的最坏运行时间为：T(n) = θ(n²)。下面给出严格的定义：

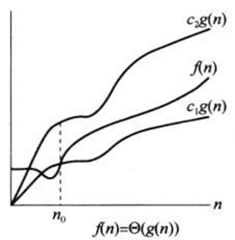
θ(g(n)) = {f(n)：存在正常量c1，c2，n0，使得对所有n ≥ n0，有0 ≤ c1 * g(n) ≤ f(n) ≤ c2 * g(n)}

通俗地讲，若存在正常数才c1，c2，使得对于足够大的n，函数f(n)能“夹入”c1*g(n)与c2*g(n)之间，则f(n)属于集合θ(g(n))（通常把f(n) ∈ θ(g(n))记为f(n) = θ(g(n))）。我们称g(n)是f(n)的一个渐进紧确界。

(2) Ο记号

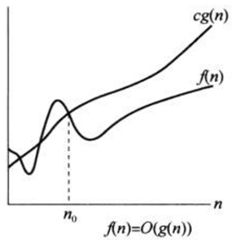
     θ记号渐进的给出了一个函数的上界和下界。当只有一个渐进上界时，使用Ο记号。下面给出Ο(g(n))的定义：

Ο(g(n)) = {f(n)：存在正常量c，n0，使得对所有n ≥ n0，有0 ≤ f(n) ≤ c * g(n)}

(3) Ω记号

     正如Ο记号提供了一个函数的渐进上界一样，Ω记号提供了一个渐进下界。下面给出Ο(g(n))的定义：

Ω(g(n)) = {f(n)：存在正常量c，n0，使得对所有n ≥ n0，有0 ≤ c * g(n) ≤ f(n) }

(4) ο记号

    Ο记号提供的渐进上界可能是也可能不是渐进紧确的。因此我们使用ο记号来表示一个非紧确的渐进上界。定义如下：

ο(g(n)) = {f(n)：对于任意的正常量c，存在常量n0，使得对所有n ≥ n0，有0  ≤ f(n) < c * g(n)}

(5) ω记号

    同上，我们用ω记号来表示一个非紧确的渐进下界。形式化的定义是：

ω(g(n)) = {f(n)：对于任意的正常量c，存在常量n0，使得对所有n ≥ n0，有0 ≤ c * g(n) < f(n) }

(6) 等式和不等式中的渐进记号

     ① 对于形如2n²+3n+1 = 2n²+θ(n)的等式的解释是：2n²+3n+1 = 2n²+f(n)，f(n) = θ(n)（f(n)  ∈ θ(n)）。

     ② 对于形如 2n² + θ(n) = θ(n²)的等式的解释是：无论怎样选择等号左边的匿名函数，总有办法开选择等号右边的匿名函数来使等式成立。

ps：以上内容均摘自《算法导论》中文译本。本人只是提取出文中个人认为比较重要的点 加入了一些个人理解仅供参考。