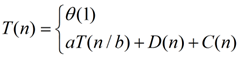算法基础——算法导论(1)

1. 写在前面

本篇博文是学习算法导论的第一次记录，主要想介绍如何去证明算法的正确性；如何去评判一种算法的好坏；以及如何去改进算法。

2. 从插入排序说起

插入排序（insert-sort）是一种十分常见的算法，我们在生活中可能就经常在使用——玩扑克。考虑我们抓牌时的场景。首先，你的右手（不考虑左撇子）会不断从桌上拿起一张扑克，然后从左往右（或从右往左）依次观察左手扑克序列中各个牌面的大小，直到找到一个合适的位置，将右手拿到的扑克插入其中，完成一次抓牌操作。在所有的扑克抓完时，你左手的扑克便是排好序的。

借助于这个思想，我们可以很容易写出插入排序的代码，下面是 Java 的实现代码：

/**
     * 插入排序
     * 
     * @param a 需要排序的数组
     */
    public static void insertSort(int[] a) {
        for (int i = 1; i < a.length; i++) {
            int j = i - 1;
            // curr 表示要插入的扑克
            int curr = a[i];
            // 要插入的扑克从左手的扑克序列最右端不断向左移动
            // 直到到了尽头或者要插入的扑克比左手某一扑克大时，就停止移动
            while (j > -1 && curr < a[j]) {
                a[j + 1] = a[j];
                j--;
            }
            a[j + 1] = curr;
        }
    }

 

2.算法证明

也许你对上述代码还有疑问，担心它是否正确。下面介绍一种叫做循坏不变式的方法来证明它是正确的。循环不变式的思想和我们高中学习的数学归纳法类似，它的证明步骤如下：

1. 找出一个式子：我们需要先找到一个式子作为目标。这个式子不能是一个只包含常量的式子，它需要在每次迭代时都在变化。我们的目的就是要证明在每次循环中，它都是成立的，并且在循环结束时，它的成立正好能证明我们的结论。

2. 初始化：在找到可能的循环不变式后，我们需要证明它在迭代开始前（或第一次迭代）就是正确的。

3.  保持：若循环不变式在当前是正确的，我们需要证明它在下一次循环结束后，也是正确的。

4. 终止：若我们给出了以上两个步骤的证明，那么有理由相信，我们的结论是正确的。并且我们称以上找出的式子叫循环不变式。

以上面的插入排序为例。显然我们可以将 a[i] 作为我们需要证明的式子。

• 初始化：在第一次迭代之前，a[i] 只有一位 a[0]，显然是排好序的；
• 保持：先假设在第 i 次迭代之前，不变式成立，即 a[0 ~ i-1] 是排好序的；在进行第 i 次迭代中，根据算法，a[i] 从 a[0~i-1] 的最右端开始不断向左移动，直到找到自己合适的位置。在这次迭代完成时（即下一次迭代前），显然 a[0 ~ i] 就是排好序的。
• 终止：我们证明了上述两个条件都是正确的。因此，在循环结束时（i = a.length - 1），a[0 ~ i] 即 a[0 ~ a.length - 1] 即数组 a ，是排好序的。

3. 算法分析

下面介绍评定算法好坏的一个维度：时间复杂度。

假定我们的算法在一种通用的单处理器计算模型——随机访问机（random-access machine，RAM）中实现。在该模型中，一些常用的计算机指令，包括算术指令（加、减、乘、除、取余、向上取整、向下取整）、数据移动指令（装入、储存、复制）和控制指令（条件与无条件转移、子程序调用与返回），它们执行所需的时间为常量。

 以上面的插入排序（insert-sort）为例：

//(c, n)，第一个参数表示该步执行一次的时间，第二个参数表示该步执行的次数。
        for (int i = 1; i < a.length; i++) { // (c1, n)
            int j = i - 1; //(c2, n-1)
            int curr = a[i]; // (c3, n-1)
            while (j > -1 && curr < a[j]) { // (c4, t2+t3+...+tn)
                a[j + 1] = a[j];// (c5, (t2-1)+(t3-1)+...+(tn-1))
                j--;// (c6, (t2-1)+(t3-1)+...+(tn-1))
            }
            a[j + 1] = curr;// (c7, n-1)
        }

它的计算总时间：

• 最佳情况：T(n) =c1 * n  + c2 * (n - 1) + c3 * (n - 1) + c4 * (n - 1) + c7 * (n - 1)= (c1 + c2 + c3 + c4 + c7) * n – (c2 + c3 + c4 + c7)。此种情况，我们可以把 T(n) 表示为 an+b，它是 n的线性函数。

• 最坏情况：T(n) = c1 * n + (c2 + c3 + c7) * (n - 1) + c4 * [n(1 + n) / 2 - 1] + (c5 + c6) * [n(1 + n) / 2] = (c4 / 2 + c5 / 2 + c6 / 2) * n² + (c1 + c2 + c3 + c7 - c4 / 2 - c5 / 2 - c6 / 2) * n – (c2 + c3 + c7 + c4)。此种情况，我们可以把 T(n) 表示为 an^2 + bn + c，它是 n 的二次函数。

更近一步，考虑到我们真正感兴趣的其实是算法运算时间的增长率（增长量级），因此可忽略低阶项和最高阶项的常系数。于是，我们直接将插入排序（insert-sort）的最佳情况运行时间记为：θ(n)，而最坏情况运行时间记为：θ(n²)。其中 θ(x) 是记录式子渐进上下界的一种表示方式，下一篇博文会详细介绍。

有时候，我们更应该多加考虑最坏情况，因为：① 最坏情况给出了一个上界，可以确保该算法不会超过某一时间；② 最坏情况往往经常出现；③ “平均情况”和最坏情况大致一样差。

4. 算法设计

当一种算法有缺陷时，需要想办法去设计改进算法。

插入排序采用了增量方法，将 a[i] 插入子数组 a[0~i-1] 中，子数组增长为：a[0~i]。

下面介绍一种叫做分治法（Divide and Conquer）的设计方法来改进插入排序算法。其思想是将原问题分解为几个规模较小的但类似于原问题的子问题，然后递归的解决这些子问题，最后合并这些子问题的解，这样能得到原问题的解。

根据分治法（Divide and Conquer）的思想，我们可以设计出一种叫做 归并排序（merge-sort）的算法，操作步骤如下：

• 分解 将待排序的具有n个元素的序列分成2个具有n / 2个元素的子序列；
• 解决 使用归并排序递归的解决2个子序列；
• 合并 合并已排序的2个子序列得到答案；

下面给出归并排序（merge-sort）的java实现代码：

/**
     * 将a[p~r]排序
     * 
     * @param a
     * @param p
     * @param r
     */
    public static void mergeSort(int[] a, int p, int r) {
        if (p < r) {
            int q = (r + p) / 2;
            mergeSort(a, p, q);
            mergeSort(a, q + 1, r);
            merge(a, p, q, r);
        }
    }

    /**
     * 合并2个已排序的序列(a[p ~ q]和a[q+1 ~ r])
     * 
     * @param a
     * @param p q >= p
     * @param q
     * @param r
     */
    public static void merge(int[] a, int p, int q, int r) {
        int[] a1 = new int[q - p + 2];
        int[] a2 = new int[r - q + 1];
        for (int i = 0; i < a1.length - 1; i++) {
            a1[i] = a[p + i];
        }
        a1[a1.length - 1] = Integer.MAX_VALUE;
        for (int i = 0; i < a2.length - 1; i++) {
            a2[i] = a[q + i + 1];
        }
        a2[a2.length - 1] = Integer.MAX_VALUE;
        int m = 0, n = 0;
        for (int i = p; i < r + 1; i++) {
            if (a1[m] < a2[n]) {
                a[i] = a1[m];
                m++;
            } else {
                a[i] = a2[n];
                n++;
            }
        }
    }

 简答解释一下合并的操作。首先，进行合并的两个数组必须已经是排好序的，这是前提。为了解释的清楚合并的过程，还是想象我们熟悉的玩扑克的场景。假设你需要将一副扑克按牌面大小排序。为了快速完成，你可能会叫上一个小伙伴来帮忙。你们先把扑克一份为二 ，各自排好自己拿到的扑克的顺序，拿在手上，为接下来的合并做准备。在合并时，你们每次都拿出自己手中牌堆最顶部的（各自牌堆中最小的）扑克，然后比较大小。谁的牌面值小，谁就将扑克放在桌面牌堆的顶部（第一次桌面是空的，直接放在桌面上）。不断重复上述过程，直到某人手中没有扑克，另一人就可以直接将其手中所有的扑克一次性放入桌面的牌堆的顶部。这时，桌面上的这堆扑克从底到顶，便是从小到大排列的。

分治法真的能提高效率么？归并排序真的优于插入排序么？下面来做分析。

设T(n)为规模为n的问题运用分治法所需的运行时间。若问题规模足够小，如对于某个常量c，n <= c，则直接求解需要常量时间，记为：θ(1)；否则，把问题分解成a个子问题，每个子问题的规模是原来的1 / b，则T(n) = a * T(n / b)，如果分解为子问题所需时间为D(n) （可记为：θ(1)），合并子问题所需的时间为C(n)（可记为：θ(n)），那么T(n)递归式为：

特别的，对于归并排序（merge-sort），

可以求得T(n) = c * n * lg n + cn，记为：θ(n * lg n)。

可见当n较大时，在最坏情况下，归并排序优于插入排序。

ps：以上内容均摘自《算法导论》中文译本。本人只是提取出文中个人认为比较重要的点，加入了一些个人理解，仅供参考。有些句子和词由于是翻译过来的，所以可能比较突兀，会意就好。