用PyTorch自动求导

从这里学习《DL-with-PyTorch-Chinese》 4.2用PyTorch自动求导

考虑到上一篇手动为由线性和非线性函数组成的复杂函数的导数编写解析表达式并不是一件很有趣的事情，也不是一件很容易的事情。这里我们用通过一个名为autograd的PyTorch模块来解决。

利用autograd的PyTorch模块来替换手动求导做梯度下降

首先模型和损失函数还是不变：

def model(t_u, w, b):
    return w * t_u + b

def loss_fn(t_p, t_c):
    squared_diffs = (t_p - t_c)**2
    return squared_diffs.mean()

然后初始化参数张量：

params = torch.tensor([1.0, 0.0], requires_grad=True)

张量构造函数的require_grad = True这个参数告诉PyTorch需要追踪在params上进行运算而产生的所有张量。换句话说，任何以params为祖先的张量都可以访问从params到该张量所调用的函数链。如果这些函数是可微的（大多数PyTorch张量运算都是可微的），则导数的值将自动存储在参数张量的grad属性中

上一篇的手动求导过程现在可以改写成这样：

loss = loss_fn(model(t_u, *params), t_c)
loss.backward()
params.grad

用autograd计算的模型的前向传播图和反向传播图：

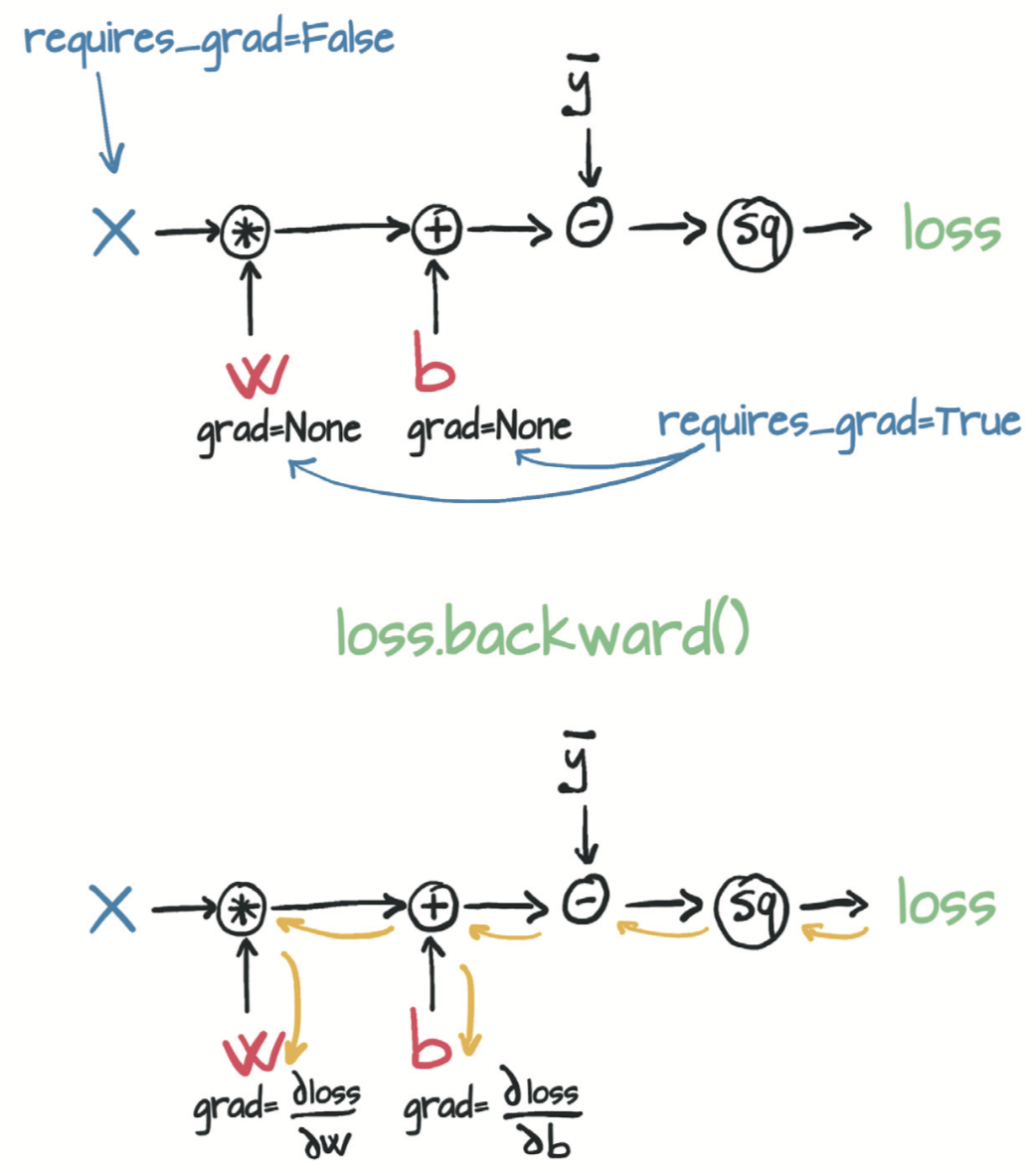
 关于梯度显示清零问题：

在这种情况下，PyTorch会在沿着整个函数链（即计算图）计算损失的导数，并在这些张量（即计算图的叶节点）的grad属性中将这些导数值累积（accumulate）起来。

警告：PyTorch的新手（以及很多经验丰富的人）经常忽视的事情：是积累（accumulate）而不是存储（store）。

警告：调用backward会导致导数值在叶节点处累积。所以将其用于参数更新后，需要将梯度显式清零。

重复调用backward会导致导数在叶节点处累积。因此，如果提前调用了backward，然后再次计算损失并再次调用backward（如在训练循环中一样），那么在每个叶节点上的梯度会被累积（即求和）在前一次迭代计算出的那个叶节点上，导致梯度值不正确。

为防止这种情况发生，你需要在每次迭代时将梯度显式清零。可以使用就地方法zero_轻松地做到这一点。

因此现在整个循环训练过程可以改写为：

def training_loop(n_epochs, learning_rate, params, t_u, t_c):
    for epoch in range(1, n_epochs + 1):
        if params.grad is not None: 
            params.grad.zero_() # 这可以在调用backward之前在循环中的任何时候完成
        t_p = model(t_u, *params)
        loss = loss_fn(t_p, t_c)
        loss.backward()
        params = (params - learning_rate * params.grad).detach().requires_grad_()
        if epoch % 500 == 0:
            print('Epoch %d, Loss %f' % (epoch, float(loss)))
    return params

优化器：

现在是时候介绍PyTorch从用户代码（例如训练循环）中抽象出来的优化策略了，以使你免于繁琐地更新模型中的每个参数。torch模块有一个optim子模块，你可以在其中找到实现不同优化算法的类。

每个优化器都有两个方法：zero_grad和step。zero_grad将构造时传递给优化器的所有参数的grad属性归零；step根据特定优化器实施的优化策略更新这些参数的值。

示例使用SGD优化器：

params = torch.tensor([1.0, 0.0], requires_grad=True)
learning_rate = 1e-5
optimizer = optim.SGD([params], lr=learning_rate)

现在使用优化器改写循环训练代码：

def training_loop(n_epochs, optimizer, params, t_u, t_c):
    for epoch in range(1, n_epochs + 1):
        t_p = model(t_u, *params)
        loss = loss_fn(t_p, t_c)
        optimizer.zero_grad()
        loss.backward()
        optimizer.step()
        if epoch % 500 == 0:
            print('Epoch %d, Loss %f' % (epoch, float(loss)))
    return params

params = torch.tensor([1.0, 0.0], requires_grad=True)
learning_rate = 1e-2
optimizer = optim.SGD([params], lr=learning_rate)

training_loop(
    n_epochs = 5000,
    optimizer = optimizer,
    params = params,
    t_u = t_un,
    t_c = t_c)

 完整代码：

#!/usr/bin/env python
# coding: utf-8

# In[1]:


import torch


# In[2]:


t_c = [0.5,  14.0, 15.0, 28.0, 11.0,  8.0,  3.0, -4.0,  6.0, 13.0, 21.0]
t_u = [35.7, 55.9, 58.2, 81.9, 56.3, 48.9, 33.9, 21.8, 48.4, 60.4, 68.4]
t_c = torch.tensor(t_c)
t_u = torch.tensor(t_u)

def model(t_u, w, b):
    return w*t_u + b

def loss_fn(t_p, t_c):
    squared_diffs = (t_p-t_c)**2
    return squared_diffs.mean()

# require_grad = True这个参数告诉PyTorch需要追踪在params上进行运算而产生的所有张量
# 换句话说，任何以params为祖先的张量都可以访问从params到该张量所调用的函数链
# 如果这些函数是可微的（大多数PyTorch张量运算都是可微的），则导数的值将自动存储在参数张量的grad属性中
params = torch.tensor([1.0, 0.0], requires_grad=True)

# 一般来讲，所有PyTorch张量都有一个初始为空的名为grad的属性：
params.grad is None  # True


# In[3]:


# 我们需要做的就是从将require_grad设置为True开始，然后调用模型，计算损失值，然后对损失张量loss调用backward：
loss = loss_fn(model(t_u, *params), t_c)
loss.backward()
params.grad


# In[9]:


'''
警告：调用backward会导致导数值在叶节点处累积。所以将其用于参数更新后，需要将梯度显式清零。
'''
def training_loop(n_epochs, learning_rate, params, t_u, t_c):
    for epoch in range(1, n_epochs+1):
        if params.grad is not None:
            params.grad.zero_()
        t_p = model(t_u, *params)
        loss = loss_fn(t_p, t_c)
        loss.backward()
        params = (params-learning_rate*params.grad).detach().requires_grad_()
        if epoch % 500 == 0:
            print('Epoch %d, Loss %f' % (epoch, float(loss)))
    return params
'''
请注意，更新参数时，你还执行了奇怪的.detach().requires_grad_()。要了解原因，请考虑一下你构建的计算图。为了避免重复使用变量名，我们重构params参数更新行：p1 = (p0 * lr * p0.grad)。这里p0是用于初始化模型的随机权重，p0.grad是通过损失函数根据p0和训练数据计算出来的。

到目前为止，一切都很好。现在，你需要进行第二次迭代：p2 = (p1 * lr * p1.grad)。如你所见，p1的计算图会追踪到p0，这是有问题的，因为(a)你需要将p0保留在内存中（直到训练完成），并且(b)在反向传播时不知道应该如何分配误差。

相反，应该通过调用.detatch()将新的params张量从与其更新表达式关联的计算图中分离出来。这样，params就会丢失关于生成它的相关运算的记忆。然后，你可以调用.requires_grad_()，这是一个就地（in place）操作（注意下标“_”），以重新启用张量的自动求导。现在，你可以释放旧版本params所占用的内存，并且只需通过当前权重进行反向传播。
'''

# In[10]:


t_un = 0.1 * t_u
training_loop(
    n_epochs = 5000,
    learning_rate = 1e-2,
    params = torch.tensor([1.0, 0.0], requires_grad=True),
    t_u = t_un,
    t_c = t_c)


# In[11]:


# 优化器
import torch.optim as optim
dir(optim)


# In[12]:


def training_loop(n_epochs, optimizer, params, t_u, t_c):
    for epoch in range(1, n_epochs + 1):
        t_p = model(t_u, *params)
        loss = loss_fn(t_p, t_c)
        optimizer.zero_grad()
        loss.backward()
        optimizer.step()
        if epoch % 500 == 0:
            print('Epoch %d, Loss %f' % (epoch, float(loss)))
    return params

params = torch.tensor([1.0, 0.0], requires_grad=True)
learning_rate = 1e-2
optimizer = optim.SGD([params], lr=learning_rate)

training_loop(
    n_epochs = 5000,
    optimizer = optimizer,
    params = params,
    t_u = t_un,
    t_c = t_c)

# Adam，你现在只需要知道它自适应地设置学习率，是一种更加复杂的优化器。此外，它对参数缩放的敏感度很低，以至于你可以使用原始（非标准化）输入t_u甚至将学习率提高到1e-1：
# In[14]:


params = torch.tensor([1.0, 0.0], requires_grad=True)
learning_rate = 1e-1
optimizer = optim.Adam([params], lr=learning_rate)

training_loop(
    n_epochs = 5000,
    optimizer = optimizer,
    params = params,
    t_u = t_u,
    t_c = t_c)


# In[15]:


# 对张量的元素进行打乱等价于重新排列其索引。randperm函数完成了这个操作：
n_samples = t_u.shape[0]
n_val = int(0.2 * n_samples)

shuffled_indices = torch.randperm(n_samples)
train_indices = shuffled_indices[:-n_val]
val_indices = shuffled_indices[-n_val:]

train_indices, val_indices # 划分结果是随机的


# In[16]:


# 你获得了可用于从数据张量构建训练集和验证集的索引：
train_t_u = t_u[train_indices]
train_t_c = t_c[train_indices]

val_t_u = t_u[val_indices]
val_t_c = t_c[val_indices]

train_t_un = 0.1 * train_t_u
val_t_un = 0.1 * val_t_u


# In[17]:


# 训练循环代码和之前一样，额外添加了评估每个epoch的验证损失以便查看是否过度拟合：
def training_loop(n_epochs, optimizer, params, 
                  train_t_u, val_t_u, train_t_c, val_t_c):
    for epoch in range(1, n_epochs + 1):
        train_t_p = model(train_t_u, *params)
        train_loss = loss_fn(train_t_p, train_t_c)

        val_t_p = model(val_t_u, *params)
        val_loss = loss_fn(val_t_p, val_t_c)

        optimizer.zero_grad()
        train_loss.backward() # 注意没有val_loss.backward因为不能在验证集上训练模型
        optimizer.step()

        if epoch <= 3 or epoch % 500 == 0:
            print('Epoch %d, Training loss %.2f, Validation loss %.2f' % (
                    epoch, float(train_loss), float(val_loss)))
    return params

params = torch.tensor([1.0, 0.0], requires_grad=True)
learning_rate = 1e-2
optimizer = optim.SGD([params], lr=learning_rate)

training_loop(
    n_epochs = 3000,
    optimizer = optimizer,
    params = params,
    train_t_u = train_t_un,
    val_t_u = val_t_un,
    train_t_c = train_t_c,
    val_t_c = val_t_c)


# In[ ]: