相关资料
https://www.cnblogs.com/dojo-lzz/p/13237686.html
文档:PBR学习笔记.note
对于之前的这篇文章中,基本了解了PBR分解后的各个子项意思,但是对于最后一个IBL的解释实际上还是有些牵强。这几天了解到了蒙特卡洛积分以及基于重要性采样的蒙特卡洛几分才算是对这部分有个比较透彻的了解。
参考资料先存下来:
生成brdf LUT的工具:https://github.com/HectorMF/BRDFGenerator
理论
PBR是基于物理的渲染,核心是从能量守恒角度将各个方向的光源进行积分。BRDF就是根据物体的各种性质经过一系列实验得到的一个双向反射分布函数来进行模拟。在之前那篇文章中,首先对于环境中已有的点光源和方向光源分别进行caculatorFinalColor处理根据diffuse和specular;
vec3 calculateFinalColor(PBRInfo pbrInputs, vec3 lightColor) { // Calculate the shading terms for the microfacet specular shading model vec3 F = specularReflection(pbrInputs); float G = geometricOcclusion(pbrInputs); float D = microfacetDistribution(pbrInputs); // Calculation of analytical lighting contribution vec3 diffuseContrib = (1.0 - F) * diffuse(pbrInputs); vec3 specContrib = F * G * D / (4.0 * pbrInputs.NdotL * pbrInputs.NdotV); // Obtain final intensity as reflectance (BRDF) scaled by the energy of the light (cosine law) return pbrInputs.NdotL * lightColor * (diffuseContrib + specContrib); }
对于环境中光源的处理已经完成了,但是前面说到PBR是对各个方向的光进行积分,即对环境中各个方向能够反射进入人眼中光都需要处理。

首先光怎么来,可以认为是从环境贴图中来,我们就认为环境贴图中每个像素颜色代表代表一个微分光源,也就是说要对环境贴图中所有纹理进行遍历求和,这个过程显然对于实时渲染时不可接受的,这么这个时候就出现了蒙特卡洛积分。蒙特卡洛积分的思想是在整个积分区间内,随机的进行有限个采样,通过采样点的均值来进行近似。
想具体了解下蒙特卡洛积分的,可以看这篇文章,这是迄今我见过最通俗易懂的文章:https://blog.csdn.net/i_dovelemon/article/details/76286192
但是呢光有基础蒙特卡罗并不行,因为我们是随机采样,每个采样点实际上对于整体的贡献度是不相同的,所以我们还需要计算每个采样点对于整体的权重情况,那么这个计算重要性的过程与蒙特卡洛结合就称为基于重要性的蒙特卡洛积分https://blog.csdn.net/i_dovelemon/article/details/76786741。
现在整个公式变成这个样子了
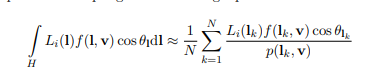
再来现在采样有了,权重有了,还有一个问题要解决就是采样的分布情况。如果都集中在高权重或低权重对整体结果的影响是很大的,所以图形学在这个过程中有专门的一个采样序列的问题。通过一个有特点的采样函数来生成一些采样点,这里使用的是Hammersley采样序列算法https://blog.csdn.net/i_dovelemon/article/details/76599923。

好了,下面来看下我们汇总后的代码(我们对于环境光来说漫反射部分实际上各个方向都是一样的,所以这里重点看镜面反射部分):
float3 SpecularIBL( float3 SpecularColor , float Roughness, float3 N, float3 V ) { float3 SpecularLighting = 0; const uint NumSamples = 1024; // 使用了1024个采样点 for( uint i = 0; i < NumSamples; i++ ) { float2 Xi = Hammersley( i, NumSamples ); // 计算一个随机采样序列 float3 H = ImportanceSampleGGX( Xi, Roughness, N ); // 将一个二维采样序列转换成三维空间中的采样方向 // 下面是计算法线、采样方向、视线等各种方向的一堆夹角 // 看上图L是从一个随机采样方向计算出得到的环境入射光源的反方向 float3 L = 2 * dot( V, H ) * H - V; float NoV = saturate( dot( N, V ) ); float NoL = saturate( dot( N, L ) ); float NoH = saturate( dot( N, H ) ); float VoH = saturate( dot( V, H ) ); if( NoL > 0 ) { // 计算环境光源颜色,envMap很可能是立方体贴图 float3 SampleColor = EnvMap.SampleLevel( EnvMapSampler , L, 0 ).rgb; // 下面是计算BRDF的specular部分的G和F,这里并没有计算D,因为在BRDF/pdf过程中,D被消除掉了。 float G = G_Smith( Roughness, NoV, NoL ); float Fc = pow( 1 - VoH, 5 ); float3 F = (1 - Fc) * SpecularColor + Fc; // Incident light = SampleColor * NoL // Microfacet specular = D*G*F / (4*NoL*NoV) // pdf = D * NoH / (4 * VoH) // 上面pdf公式可以看出重要性跟粗糙度、法线与采样方向、视线与采样方向相关的。粗糙度是一个经过物理实验测量的值 SpecularLighting += SampleColor * F * G * VoH / (NoH * NoV); } } return SpecularLighting / NumSamples; // 求和再取均值就是蒙特卡罗积分的体现 }
上文中讲到了先有采样序列,然后是将一个二维随机数映射为采样方向,下面就来看下这个过程:
要理解这个,得要有立体角的概念,这个概念如果不明白可以搜一搜,讲的挺多的。
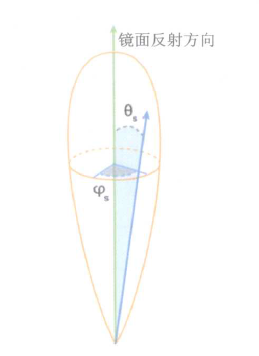
对于一个微分立体角来说,要确定一个向量只需要有两个量,phi和theta;这两个量就是通过上文中的采样序列生成的。下面要做的就是把这微分立体角坐标转换成三维空间坐标。(注意:图片中说的镜面反射方向应该是法向量方向,这里可能是GPU GEM中文作者翻译错误了)
float3 ImportanceSampleGGX( float2 Xi, float Roughness, float3 N ) { float a = Roughness * Roughness; float Phi = 2 * PI * Xi.x; // 水平方向的phi // theta不知道是怎么计算出来的,可能也是根据一个数学理论来计算的,这里可以看到有将粗糙度考虑进去 float CosTheta = sqrt( (1 - Xi.y) / ( 1 + (a*a - 1) * Xi.y ) ); float SinTheta = sqrt( 1 - CosTheta * CosTheta ); float3 H; // 根据微分立体角坐标求得以该表面为原点,镜面反射方向为微分球的局部三维坐标系 H.x = SinTheta * cos( Phi ); H.y = SinTheta * sin( Phi ); H.z = CosTheta; // 求表面切空间的的基底,切空间基底向量坐标系为世界坐标系 float3 UpVector = abs(N.z) < 0.999 ? float3(0,0,1) : float3(1,0,0); float3 TangentX = normalize( cross( UpVector, N ) ); float3 TangentY = cross( N, TangentX ); // Tangent to world space // 下面这个操作的前提是需要微分球的纵轴方向要与该点法向量的轴重合才行,而不是图片中说的镜面反射方向,这里可能是GPU GEM中文作者翻译错误了 // 因为微分球转换的三维坐标与且空间重合,所以这里是将微分三维坐标进行向量分解,最终得到一个三维空间坐标下的单位向量 return TangentX * H.x + TangentY * H.y + N * H.z; }
可以看到这是在实时渲染情况下的计算过程,根据GPU 精粹3中第20章的结果来看,并不用1024次采样只需要40几次即可。
这种实时渲染的优点真的实时渲染,不需要提前生成BRDF 的LUT查找表,但问题也是每帧都这么计算还是很耗费性能,所以后来的大牛各种研究,就是我们在PBR学习笔记中看到的那部分,在IBL这部分直接读取纹理。
其实在图形学继续深入的研究方向比如仿真、光线追踪,大部分处理过程都是一个近似过程,这也是为什么像GPU精粹、GPU Pro、GPU Zen中经常开头一复杂积分,到了最后代码过程其实还是简单的加减乘除和循环。所以在整个仿真的过程中,首先通过物理理论研究完成完整计算公式,后续进行一步步近似和简化,逐渐转化成GPU可执行的代码程序。这也是图形学奇高的门槛,一个数学公式让人望而生畏,转头就跑。好了下面说一下怎么进行进一步的近似处理。
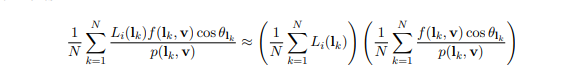
经过一系列数学研究之后拆成了两个公式。拆成这两部分的优势是,两部分都可以做预处理,通过程序提前写入纹理中,实时渲染只需要去纹理中去查询即可,做简单的加减乘除。
前一部分可以预处理成跟roughness和cos(v)相关的光照颜色,原理跟上面实时渲染差不多,取了采样了一批环境纹理的颜色,取均值。
float3 PrefilterEnvMap( float Roughness, float3 R ) { float3 N = R; float3 V = R; float3 PrefilteredColor = 0; const uint NumSamples = 1024; for( uint i = 0; i < NumSamples; i++ ) { float2 Xi = Hammersley( i, NumSamples ); float3 H = ImportanceSampleGGX( Xi, Roughness, N ); float3 L = 2 * dot( V, H ) * H - V; float NoL = saturate( dot( N, L ) ); if( NoL > 0 ) { PrefilteredColor += EnvMap.SampleLevel( EnvMapSampler , L, 0 ).rgb * NoL; TotalWeight += NoL; } } return PrefilteredColor / TotalWeight; }
第二部分,最终而后半部分可以转化为一个kx+b的线性函数,这里,只有x未知(可以认为这里的x是物体的specularColor),而k,b只跟roughness和cos(v)有关。而且roughness和cos(v)都在[0,1]之间,所以,我们可以生产一张如下的纹理,建立一张映射表,通过roughness和cos直接找到对应的k,b值,省去中间大量的采样计算。当然,纹理越大,越精确,但毕竟只是[0,1]之间的插值,所以是近似值。
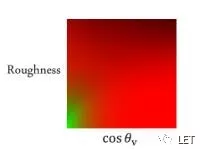
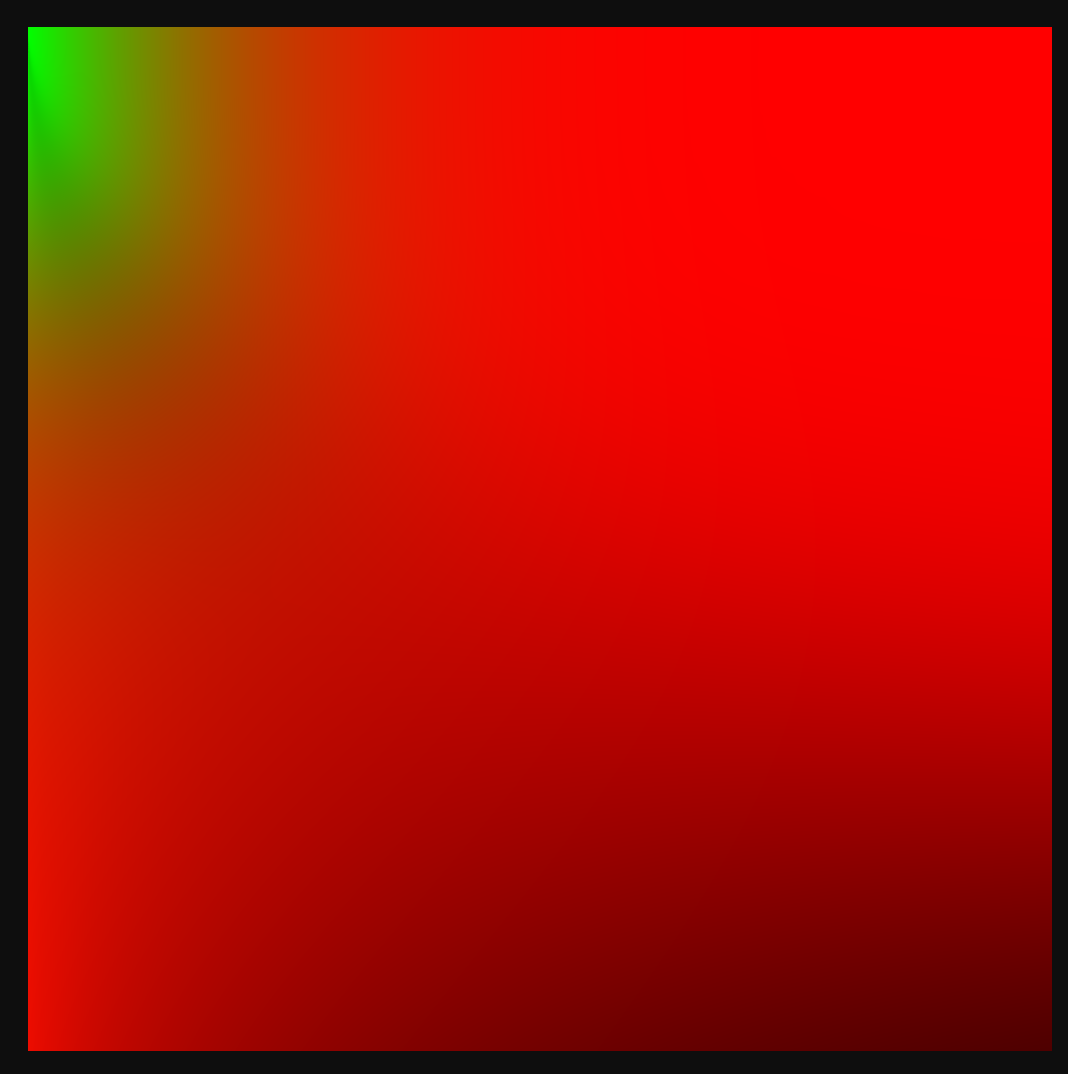
虽然大部分地方显示的是上面的图,但是在这个库中https://github.com/KhronosGroup/glTF-Sample-Viewer/tree/glTF-WebGL-PBR,使用的是下面的图,看到y轴刚好反了下:https://github.com/KhronosGroup/glTF-Sample-Viewer/blob/master/assets/images/lut_ggx.png
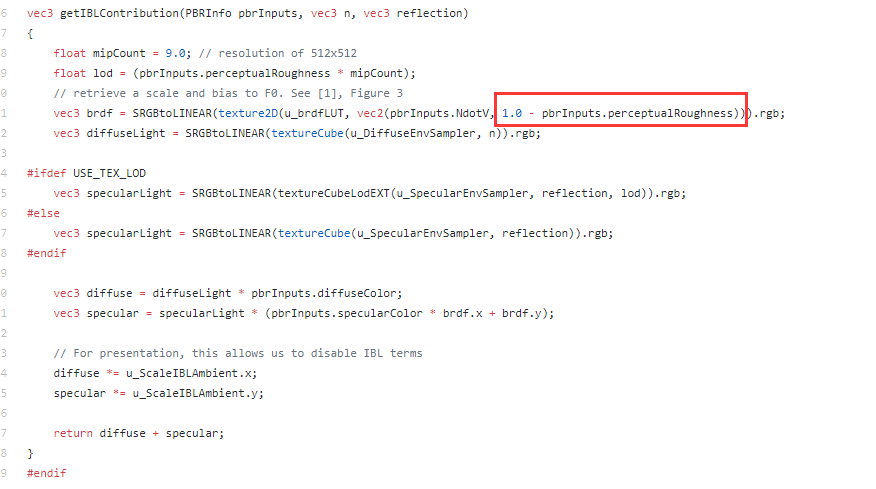
而在上一期文章中,获取brdf的代码中给纹理的坐标也确实做了1减的处理
好,回过头来,根据UE4的方案代码如下:
float2 IntegrateBRDF( float Roughness, float NoV ) { float3 V; V.x = sqrt( 1.0f - NoV * NoV ); // sin V.y = 0; V.z = NoV; // cos float A = 0; float B = 0; const uint NumSamples = 1024; for( uint i = 0; i < NumSamples; i++ ) { float2 Xi = Hammersley( i, NumSamples ); float3 H = ImportanceSampleGGX( Xi, Roughness, N ); float3 L = 2 * dot( V, H ) * H - V; float NoL = saturate( L.z ); float NoH = saturate( H.z ); float VoH = saturate( dot( V, H ) ); if( NoL > 0 ) { float G = G_Smith( Roughness, NoV, NoL ); float G_Vis = G * VoH / (NoH * NoV); float Fc = pow( 1 - VoH, 5 ); A += (1 - Fc) * G_Vis; B += Fc * G_Vis; } } return float2( A, B ) / NumSamples; }
这里有个库,可以用来生成这种查找表:https://github.com/HectorMF/BRDFGenerator
那么按照UE4的论文,根据近似公式之后,这部分IBL的着色器代码变为:
float3 ApproximateSpecularIBL( float3 SpecularColor , float Roughness, float3 N, float3 V ) { float NoV = saturate( dot( N, V ) ); float3 R = 2 * dot( V, N ) * N - V; float3 PrefilteredColor = PrefilterEnvMap( Roughness, R ); float2 EnvBRDF = IntegrateBRDF( Roughness, NoV ); return PrefilteredColor * ( SpecularColor * EnvBRDF.x + EnvBRDF.y ); }
可以看到完美对应近似公式,上面说的第二部分拆成了kx+b的形式
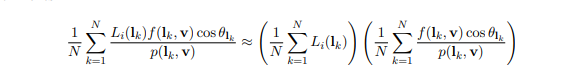
在PBR学习笔记1文章中,可以看到那里的处理方式,除了specular外还考虑了diffuseLight,也就是需要烘焙一张diffuseLight的纹理,这个纹理只跟法向量有关
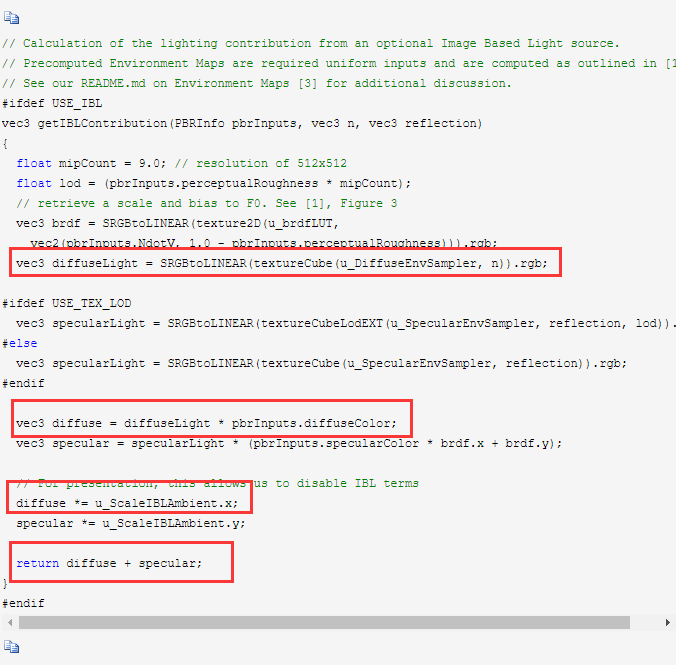
那么IBL这部分基本介绍完了,另外需要注意的是,BRDF有很多种实现方式,生成LUT也不一样最常见的是上面那种红绿的形式,另外还有:
有这个模样的,

以及这个模样的:

可以在这个库里看到:
对于BRDF中的FDG几个方面也有不同的实现,比如考虑了各向异性情况的,都在上面那个链接中,可以看一下。
如果有耐心看完,并把PBR研究透,基本也是开始摸到了光线追踪的门槛
