树状数组的功能和线段树一样。但是,这个东西是真的好写@。@
学习的博客:树状数组
树状数组主要的话可以实现三个功能①单点修改,区间查询②区间修改,单点查询.3、区间修改,区间查询。树状数组和线段树思想有点像,就是通过某个点的值来代替区间值,实现区间的运算。
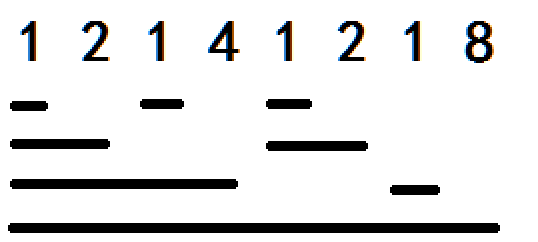
首先,一个很重要的操作是(x&-x)这个式子的结果是"从低位向高位数,第一个数字1"。我们将(x&-x)作为x管理的区间长度,如图所示。这个时候,我们发现x+(x&-x)的这个值所管理的区间也会到x,那么这样递归下去就可以将所有管理x的区间都改变值(改变操作)。求和时则不断向下递归,就能求出区间和。//接下来代码要不要加上原数组的值要视情况而定。
1 void add(int x,int num) 2 { 3 for(;x<=MAX_N;x+=(x&-x)) 4 tree[x] += num; 5 } 6 int sum(int x) 7 { 8 int s = 0; 9 for(;x>0;x-=(x&-x)) 10 s += tree[x]; 11 return s; 12 }
1、单点修改,区间查询:
每次改变点的值,再sum减一下就好了。sum(a)-sum[b-1]。(是b-1,因为求得是闭区间的和)
关于后两种方法,另一个博客写的比较清晰:树状数组2
2、区间修改,单点查询:(注意这里只能单点查询)
思想其实是化区间修改为点修改(这里的思想有点像是求前缀和)。要在(l,r)区间+k,则在l位置+k表示l及后面的位置都加了k,再在r+1的位置-k,表示从r+1开始的位置都减了k,这样其实就实现了区间的修改。把区间[L,R]的数都加上X的操作就变成了两个点修改:B[L]+=X 和 B[R+1]-=X; //这里是简写,还需要更新它们的父节点。(sum[x]);
3、区间修改,区间查询:(引用别人吧@。@)
首先引入delta数组 delta[i]表示区间 [i, n] 的共同增量 于是修改区间 [l, r] 时修改 delta[l] 和 delta[r + 1] 即可(就是差分的思路)。查询的时候是查询区间 [l, r] 的和 即sum[r] - sum[l - 1] 所以现在的问题是求sum[i]。
1 sum[i] = a[1]+...+a[i] + delta[1]*i + delta[2]*(i - 1) + delta[3]*(i - 2)+...+delta[i]*1 // a[i]为原始数组 2 = presum( a[x] ) + presum( delta[x] * (i + 1 - x) ) 3 = presum( a[x] ) + (i + 1) * presum( delta[x] ) - presum( delta[x] * x )
其中 sigma( a[x] ) 是可以预处理出来的 于是只需要维护 delta[x] 与 delta[x] * x 的前缀和(作为两个树状数组就可以了)
用两个树状数组,分别叫做d和s,d维护差分,s维护x*d[x]。
①进行区间修改操作时:
update(d,l,x);update(d,r+1,-x);
update(s,l,x*l);update(s,r+1,-x*(r+1));
②进行区间查询操作时:
sum(L,R)=sum(1,R)-sum(1,L-1)
sum(1,L-1)=L*query(d,L-1)-query(s,L-1)
sum(1,R)=(R+1)*query(d,R)-query(s,R)