题解：2018级算法第五次上机 小面包

题目描述：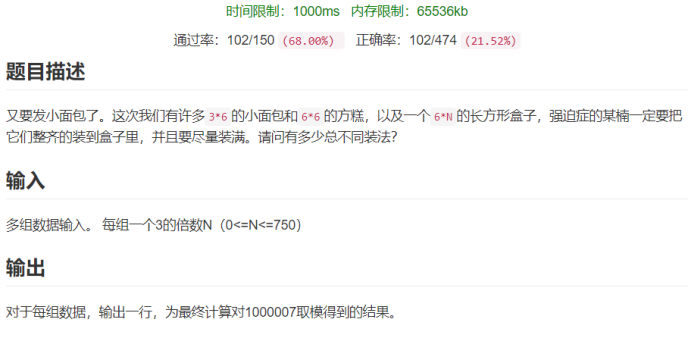

 

样例：

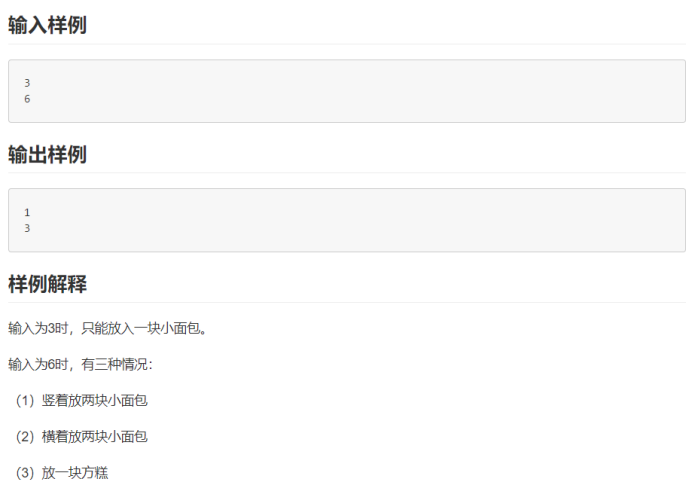
实现解释：

斐波那契的简易变形

知识点：

斐波那契，递推

　　首先对题目描述进行简化：有一个2*N的矩形，需要用无限个1*2和2*2的方块装满这个矩形，N最小为0最大为250（都除以三）。

　　则所需要做的就是从N为0一直递增到250即可，在开始递推前先设置初值：N为0，放不下所以choise[0]=0，N为1，只能1*2的方块横放，所以choice[1]=1，N为2，可以两个1*2横放，两个1*2竖放，可以一个2*2放，choice[2] =3。

　　当N大于2时，很显然可以依靠N-1，N-2两种情况得出N情况的情况种类，对N-1，多的1只能1*2横放，所以choice[N]+=choice[N-1]，对N-2，可能会率先想到三种所以+=3*choice[N-2]即可，但是这里就有一个需要考虑的，这三种情况中有一种是两个1*2横放，因此会和N-1的那种情况有重合，因此在N-2再向上增加上只能两种：一个2*2或两个1*2竖放。因此还需要choice[N-2]*2。

　　由此便可得递推公式：choice[i]+=choice[i-1]+2*choice[i-2]。

　　注意取模运算每次都要进行即可。

坑点：

递推时对三种方法不重复选择的实现，取模

完整代码：

其实非常短，毕竟斐波那契

#include<iostream>
using namespace std; 
#define MOD 1000007
long long choice[251];
int main()
{
    ios::sync_with_stdio(false);
    int n;
    choice[0] = 0;
    choice[1] = 1;
    choice[2] = 3;
    for(int i = 3;i<=250;i++)
    {
        choice[i] += choice[i-1];
        choice[i]%=MOD;
        choice[i] += (2*choice[i-2])%MOD;
        choice[i]%=MOD;
    }
    while(cin >> n)
    {
        n/=3;
        cout << choice[n]%MOD << '
';
    }
    return 0;
}